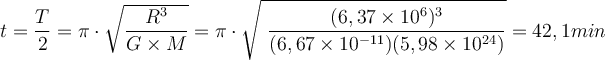Physik 06 - Gravitation
Abschnittsübersicht
-
Die Gravitation ist für das Gewicht der Körper verantwortlich, sie verursacht ihren Fall in der Nähe der Erde, was den Mond in seiner Umlaufbahn um die Erde hält, alle Planeten, die mit der Sonne verbunden sind, und ist ein allgemeines (universelles) Phänomen, das sich manifestiert zwischen zwei beliebigen materiellen Objekten. Diese brillante Idee, die Newton im Alter von 23 Jahren formulierte, war grundlegend für die empirischen Gesetze, die Kepler vorgeschlagen hatte, um die systematischen und präzisen astronomischen Daten von Nicolas Copernicus und Tycho Brahe zu erklären. Das Newtonsche Gravitationsgesetz besagt, dass jeder Körper einen anderen mit einer Kraft anzieht, die proportional zur Masse der beiden Körper und umgekehrt proportional zum Quadrat der Entfernung ist, die sie trennt.
Dieses Gesetz gilt streng genommen nur für Punktmassen, aber wir werden zeigen, wie man es anwenden kann, um die Kraft zu berechnen, die ein großer Körper auf einen anderen ausübt. Wir werden feststellen, dass bei Körpern mit kugelförmiger Massenverteilung die Kraft dieselbe wäre, als wenn die Massen in einem Zentrum konzentriert wären. Eine wichtige Eigenschaft der Gravitationskraft ist, dass sie eine Zentralkraft ist, d. h. ihre Wirkungslinie verläuft durch einen festen Punkt und sie übt um diesen Punkt herum kein Drehmoment aus, daher bleibt der Drehimpuls erhalten. Darüber hinaus ist die Gravitationskraft konservativ und bietet sich für eine Beschreibung in Form von potentieller Energie an.
Die Erhaltung von Energie und Drehimpuls wird es uns ermöglichen zu zeigen, dass die Bahn eines Planeten oder Satelliten, der sich unter dem Einfluss der Schwerkraft bewegt, im Allgemeinen eine Ellipse ist, deren Kraftzentrum in einem der Brennpunkte liegt.
Am Ende dieses Modul solltest du:
- Keplers drei Gesetze verstehen
- Newtons universelles Gravitationsgesetz kennen
- Schwerkraft in der Nähe der Erdoberfläche analysieren
- potentielle Energie der Gravitation verstehen
- Energien in der Bewegung von Satelliten kennen
-
-
Gravitation und Zentralkräfte
Zentrale Kräfte.
Eine zentrale Kraft ist jede Kraft (anziehend oder abstoßend), deren Richtung immer durch einen festen Punkt geht. Beispiele für Zentralkräfte sind die von der Sonne auf einen Planeten ausgeübte Gravitationskraft und die elektrische Kraft zwischen zwei geladenen Teilchen.
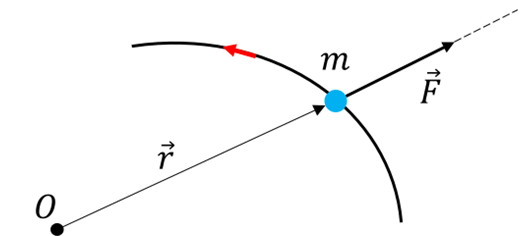
Zentrale Kräfte. G. Jimenez Da die Richtung der Kraft immer durch einen Punkt
 geht, bleiben
geht, bleiben  und
und 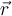 parallel und das Drehmoment aufgrund dieser Kraft relativ zu
parallel und das Drehmoment aufgrund dieser Kraft relativ zu  ist Null.
ist Null.Wenn sich also ein Körper unter der Wirkung einer Zentralkraft bewegt, ist der Drehimpuls relativ zum Kraftzentrum eine Bewegungskonstante.
Keplers drei Gesetze.
Vor der Formulierung des Gesetzes der universellen Gravitation durch Newton hatte Kepler drei empirische Gesetze formuliert, die auf astronomischen Beobachtungen basierten, die die Bewegung der Planeten um die Sonne erklärten.
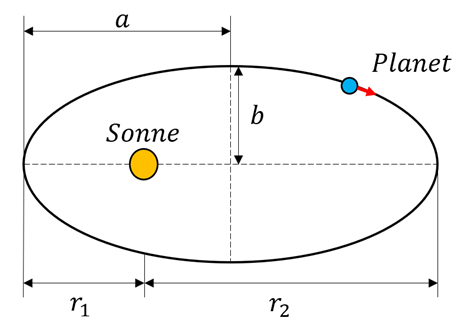
- Keplers 1. Gesetz: Bahngesetz.
Alle Planeten bewegen sich auf elliptischen Bahnen mit der Sonne in einem Brennpunkt. Erinnern Sie sich, dass eine elliptische Umlaufbahn durch zwei Parameter beschrieben werden kann: die große Halbachse a und die Exzentrizität e.
Eine Kreisbahn ist der Spezialfall einer Ellipsenbahn ohne Exzentrizität (e=0), in diesem Fall fallen die beiden Brennpunkte im Kreismittelpunkt zusammen.
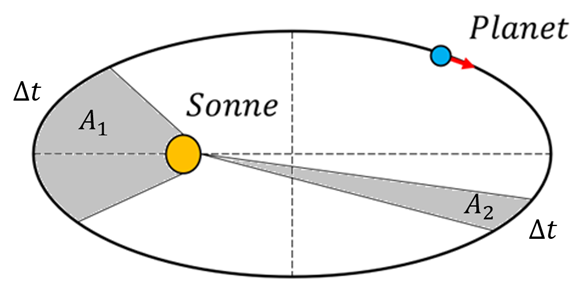
Keplers 1. Gesetz. G.Jimenez - Keplers 2. Gesetz: Gesetz der Flächen
Der Radiusvektor, der die Sonne mit jedem Planeten verbindet, überstreicht in gleichen Zeiten gleiche Flächen.
Nach diesem Gesetz bewegt sich der umkreisende Planet in Sonnennähe schneller als in Sonnenferne. Das Flächengesetz folgt daraus, dass die Schwerkraft eine zentrale Kraft ist und daher der Drehimpuls erhalten bleibt.
Keplers 2. Gesetz. G.Jimenez - Keplers 3. Gesetz: Gesetz der Perioden.
Das Quadrat der Umlaufzeit jedes Planeten um die Sonne ist proportional zur dritten Potenz der großen Halbachse der Ellipsenbahn.
Wobei
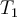 und
und 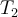 die Perioden oder Zeiten darstellen, die für eine Umdrehung um die Sonne erforderlich sind, und
die Perioden oder Zeiten darstellen, die für eine Umdrehung um die Sonne erforderlich sind, und 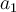 und
und 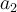 die großen Halbachsen oder mittleren Entfernungen von der Sonne sind.
die großen Halbachsen oder mittleren Entfernungen von der Sonne sind. -
Gravitationsgesetz
Newtonsche Gravitationsgesetz
Das Newtonsche Gravitationsgesetz besagt, dass jeder Punktkörper der Masse
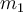 eine Anziehungskraft auf einen anderen der Masse
eine Anziehungskraft auf einen anderen der Masse 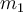 ausübt, eine Anziehungskraft auf einen anderen der Masse
ausübt, eine Anziehungskraft auf einen anderen der Masse 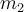 ausübt, die proportional zu den Massen der Körper und umgekehrt proportional zum Abstand
ausübt, die proportional zu den Massen der Körper und umgekehrt proportional zum Abstand 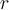 ist, der sie trennt. :
ist, der sie trennt. :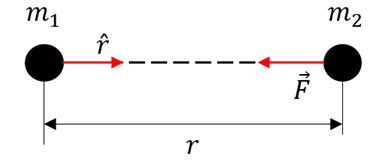
Newtosche Gravitationsgesetz. G. Jimenez Der Einheitsvektor
 hat seinen Ursprung in dem Teilchen, das die Kraft ausübt, und das Zeichen (-) zeigt an, dass die Kraft anziehend ist. Die von
hat seinen Ursprung in dem Teilchen, das die Kraft ausübt, und das Zeichen (-) zeigt an, dass die Kraft anziehend ist. Die von  auf
auf  ausgeübte Kraft hat gemäß dem dritten Newtonschen Gesetz die gleiche Größe und Richtung wie
ausgeübte Kraft hat gemäß dem dritten Newtonschen Gesetz die gleiche Größe und Richtung wie 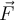 , aber die entgegengesetzte Richtung.
, aber die entgegengesetzte Richtung.Der vorige Ausdruck gilt für Punktkörper. Handelt es sich um ausgedehnte Objekte, so werden diese in infinitesimale Massenelemente zerlegt. Dies war einer der Beweggründe, dass Newton die Differential- und Integralrechnung erfinden musste und damit die Gravitationskraft einer festen Kugel an einem externen Punkt berechnen konnte.
Das newtonsceh Gravitationsgesetz für starre Körper. G. Jimenez Der nachfolgende Link führt zu einer externen Internetseite, die ggf. andere Datenschutzvorgaben erfüllt als wir es auf dieser Plattform tun. Dabei können Daten von dir übertragen und weiterverarbeitet werden. Wenn du dich allgemein zum Thema Datenschutz erkundigen möchtest, empfehlen wir dir die Erklärvideos der Initiative Datenschutz geht zur Schule.Klicke 👉 hier, um auf die Simulation über das Gravitationsgesetz zuzugreifen 😀 🏃💨
Probiere in der Einführung einmal aus,, wie die Kraft von der Auslenkung der Masse abhängt. Prüfe und sieh interaktiv, wie groß die Kraft der Gravitation ist, die Wirkrichtung und die Gleichgewichtslage des Systems.Prinzip der Superposition.
Die Gravitationskraft gehorcht dem Überlagerungsprinzip; dies ist die Gesamtkraft auf ein Teilchen i ist die Summe der Kräfte, die von den anderen Teilchen auf dieses unabhängig voneinander ausgeübt werden.
Kraft einer Kugelschale
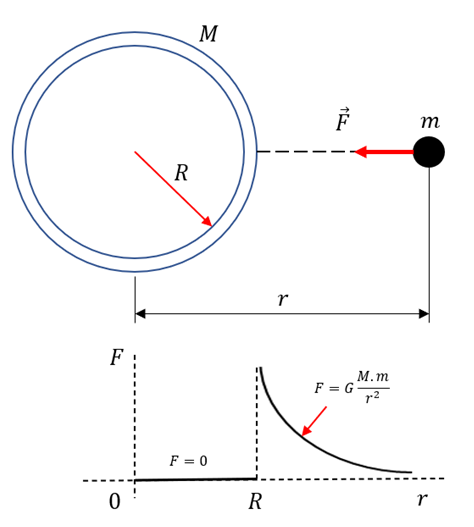
Wenn ein Teilchen der Masse
 durch Kraft von einer gleichmäßigen Kugelschale der Masse
durch Kraft von einer gleichmäßigen Kugelschale der Masse  und dem Radius
und dem Radius 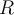 lokalisiert wird, zieht die Schale das Teilchen an, als ob die Masse der Schale in ihrem Zentrum konzentriert wäre.
lokalisiert wird, zieht die Schale das Teilchen an, als ob die Masse der Schale in ihrem Zentrum konzentriert wäre.Befindet sich das Teilchen innerhalb der Hülle, ist die Kraft auf es null.
Kraft einer Kugelschale .G. Jimenez Kraft einer festen Kugel
Befindet sich ein Teilchen der Masse
 außerhalb einer gleichförmigen Kraft der Masse
außerhalb einer gleichförmigen Kraft der Masse  und des Radius
und des Radius 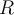 , zieht die Kugel das Teilchen an, als wäre die Masse der Kugel in ihrem Zentrum konzentriert. Dies folgt, wenn wir die feste Kugel als eine Ansammlung konzentrischer Kugelschalen betrachten.
, zieht die Kugel das Teilchen an, als wäre die Masse der Kugel in ihrem Zentrum konzentriert. Dies folgt, wenn wir die feste Kugel als eine Ansammlung konzentrischer Kugelschalen betrachten.Wenn sich das Teilchen der Masse
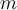 innerhalb der festen homogenen Kugel der Masse
innerhalb der festen homogenen Kugel der Masse 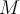 befindet, wird die Kraft auf m nur von dem Massenanteil
befindet, wird die Kraft auf m nur von dem Massenanteil 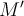 verursacht, der in der Kugel mit dem Radius
verursacht, der in der Kugel mit dem Radius 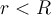 enthalten ist.
enthalten ist.Wobei wir die Masse
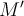 aus dem Volumenverhältnis
aus dem Volumenverhältnis 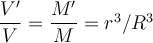 ersetzt haben. Wenn die Kugel nicht gleichmäßig wäre, sondern eine Dichte
ersetzt haben. Wenn die Kugel nicht gleichmäßig wäre, sondern eine Dichte 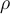 hätte, die nur eine Funktion von
hätte, die nur eine Funktion von 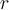 ist (Masse mit Kugelsymmetrie),
ist (Masse mit Kugelsymmetrie), 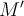 wird dann aus dem Volumenintegral berechnet.
wird dann aus dem Volumenintegral berechnet.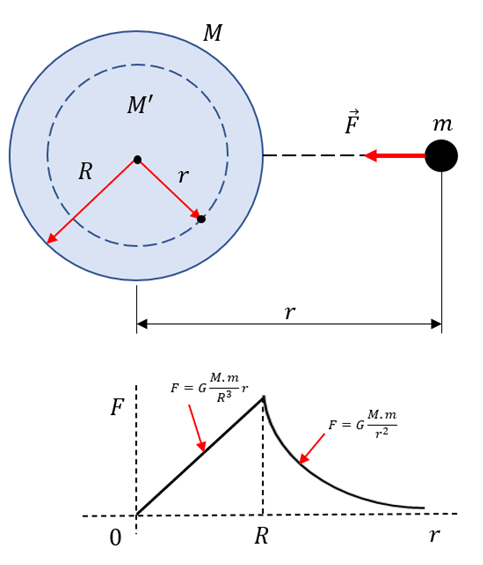
Kraft einer festen Kugel. G. Jimenez -
Das Gravitationsfeld
Um die Tatsache zu beschreiben, dass zwischen entfernten Körpern eine anziehende Gravitationskraft ausgeübt wird, wird die Idee eingeführt, dass jeder Körper den ihn umgebenden Raum verändert, indem er ein Gravitationsfeld erzeugt. Wenn wir ein Zeugenteilchen an einem bestimmten Punkt platzieren, interagiert es mit dem Gravitationsfeld, das dort aufgrund der Anwesenheit anderer Körper vorhanden ist. Das Gravitationsfeld
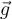 an einem Punkt im Raum ist definiert als die Gravitationskraft pro Masseneinheit.
an einem Punkt im Raum ist definiert als die Gravitationskraft pro Masseneinheit.Wobei
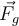 die Gravitationskraft auf das Zeugenteilchen der Masse
die Gravitationskraft auf das Zeugenteilchen der Masse 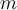 aufgrund aller anderen Körper ist. Es ist wichtig klarzustellen, dass, obwohl
aufgrund aller anderen Körper ist. Es ist wichtig klarzustellen, dass, obwohl 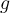 Beschleunigungseinheiten
Beschleunigungseinheiten 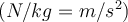 hat, das Gravitationsfeld ein anderes Konzept als das Konzept der Beschleunigung ist.
hat, das Gravitationsfeld ein anderes Konzept als das Konzept der Beschleunigung ist.Ist die Feldstärke an einem Punkt im Raum bekannt, lässt sich die Kraft bestimmen, die er auf ein Teilchen der Masse
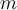 ausübt, also sein Gewicht,
ausübt, also sein Gewicht, 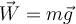 .
.Die Erdbeschleunigung nahe der Erdoberfläche.
Die von der Erde auf einen Körper der Masse
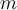 in einer bestimmten Höhe
in einer bestimmten Höhe 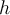 über der Erdoberfläche ausgeübte Kraft ist:
über der Erdoberfläche ausgeübte Kraft ist:Wenn die einzige Kraft, die auf einen Körper wirkt, die Gravitation ist, wird er mit einer Beschleunigung frei fallen.
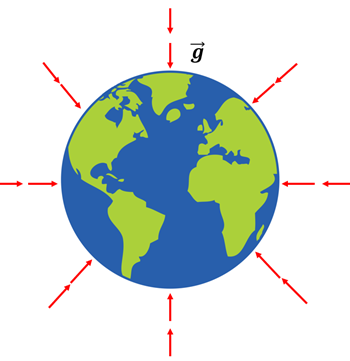
Erdbeschleunigung. G.Jimenez Gravitationspotential Energie.
Die Schwerkraft ist konservativ und daher können wir eine Potentialenergie-Skalarfunktion
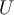 definieren:
definieren:Es ist zweckmäßig, den "Referenznullpunkt" für die potentielle Energie zu wählen, wobei der Anfangspunkt A im Unendlichen liegt. Wenn sich also ein Teilchen der Masse
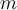 von unendlich zu einem Abstand
von unendlich zu einem Abstand 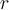 von dem Teilchen der Masse
von dem Teilchen der Masse 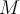 bewegt, ist seine potenzielle Gravitationsenergie:
bewegt, ist seine potenzielle Gravitationsenergie:Wir sehen, dass die Gravitationspotentialenergie im Unendlichen Null ist und mit abnehmendem Abstand
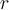 zunehmend negativ wird (abnimmt).
zunehmend negativ wird (abnimmt).Variation der potentiellen Energie in der Nähe der Erdoberfläche.
Die potenzielle Energie, die einem Teilchen der Masse
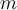 an der Erdoberfläche und in einer Höhe
an der Erdoberfläche und in einer Höhe 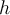 darüber zugeordnet ist, beträgt jeweils:
darüber zugeordnet ist, beträgt jeweils:Die Änderung der potentiellen Energie ist:
Wenn
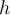 , dann
, dann 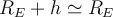 und man erhält den bekannten Ausdruck für die Variation der potentiellen Energie mit der Höhe.
und man erhält den bekannten Ausdruck für die Variation der potentiellen Energie mit der Höhe.Fluchtgeschwindigkeit.
Angenommen, ein Objekt der Masse m wird von der Erdoberfläche abgeschossen. Durch energetische Überlegungen können wir den Mindestwert seiner Anfangsgeschwindigkeit ve finden, für den das Objekt dem Gravitationsfeld der Erde entkommen würde. Anwendung der Erhaltung der gesamten mechanischen Energie im Moment des Starts und bei unendlicher Trennung.
Die Fluchtgeschwindigkeit ist für alle Körper (beliebiger Masse m) gleich und unabhängig von der Richtung der Anfangsgeschwindigkeit.
Fluchtgeschwindigkeit. G. Jimenez Energie in der Bewegung von Satelliten.
Angenommen, ein Objekt wird mit unterschiedlichen Geschwindigkeiten horizontal von der Erdoberfläche geschleudert.
Wenn die Geschwindigkeit des Objekts größer ist als die Fluchtgeschwindigkeit
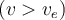 , ist seine Gesamtenergie positiv
, ist seine Gesamtenergie positiv 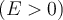 und das Objekt wird einer Hyperbel folgend von der Erde entkommen. Wenn die Geschwindigkeit des Objekts gleich der Fluchtgeschwindigkeit
und das Objekt wird einer Hyperbel folgend von der Erde entkommen. Wenn die Geschwindigkeit des Objekts gleich der Fluchtgeschwindigkeit 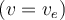 ist, seine Gesamtenergie Null ist
ist, seine Gesamtenergie Null ist 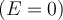 , wird das Objekt von der Erde entkommen und eine Parabel beschreiben. Wenn die Geschwindigkeit des Objekts geringer ist als die Fluchtgeschwindigkeit
, wird das Objekt von der Erde entkommen und eine Parabel beschreiben. Wenn die Geschwindigkeit des Objekts geringer ist als die Fluchtgeschwindigkeit 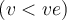 , ist seine Gesamtenergie negativ
, ist seine Gesamtenergie negativ 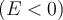 , das Objekt wird an die Erde gebunden und seine Bahn wird eine Ellipse (oder ein Kreis) sein. Wenn seine Geschwindigkeit sehr klein ist
, das Objekt wird an die Erde gebunden und seine Bahn wird eine Ellipse (oder ein Kreis) sein. Wenn seine Geschwindigkeit sehr klein ist 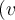 , schneidet die elliptische Umlaufbahn die Erde und der Satellit kollidiert mit ihrer Oberfläche.
, schneidet die elliptische Umlaufbahn die Erde und der Satellit kollidiert mit ihrer Oberfläche.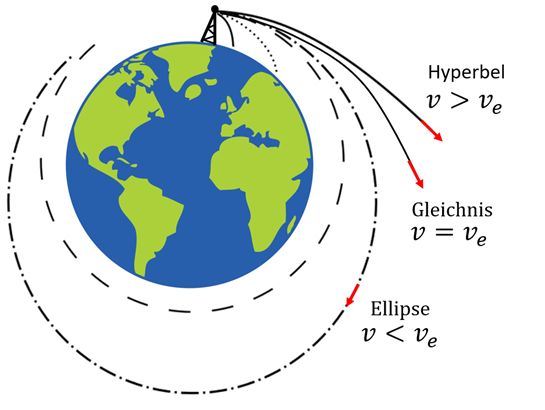
Fluchtgeschwindigkeit. G.Jimenez Flugbahnen eines Teilchens, das horizontal über die Erdoberfläche geschleudert wirdTräge Masse und Gravitationsmasse.
Die Eigenschaft eines Körpers, die für seine gravitative Wechselwirkung mit anderen Körpern verantwortlich ist, wird schwere Masse genannt. Das ist die Masse, die wir messen, wenn wir die Gewichte zweier Körper mit einer Waage vergleichen. Andererseits wird die Eigenschaft des Körpers, die seinen Widerstand gegen Beschleunigung quantifiziert, als Trägheitsmasse bezeichnet. Dies ist die Masse, auf die sich das zweite Newtonsche Gesetz
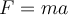 bezieht.
bezieht.Die Äquivalenz der beiden Massenarten ist nicht offensichtlich, aber es wurde kein numerischer Unterschied zwischen ihnen experimentell festgestellt. Die zahlenmäßige Gleichheit zwischen schwerer Masse und träger Masse führte Einstein zu dem Schluss, dass es keinen grundsätzlichen Unterschied zwischen einem Gravitationsfeld und einem beschleunigenden Bezugssystem gibt. Das ist das sogenannte Äquivalenzprinzip, das die Grundlage seiner Allgemeinen Relativitätstheorie bildet.
-
Beispiele: Gravitation
1) Es gibt einen Punkt zwischen Erde und Mond, an dem sich die Anziehungskraft beider auf einem Raumschiff ausgleicht. An welchem Punkt auf der Verbindungslinie zwischen Erde und Mond ist die Gravitationskraft auf ein Objekt gleich Null?
Ignorieren Sie die Anwesenheit der Sonne und der anderen Planeten.
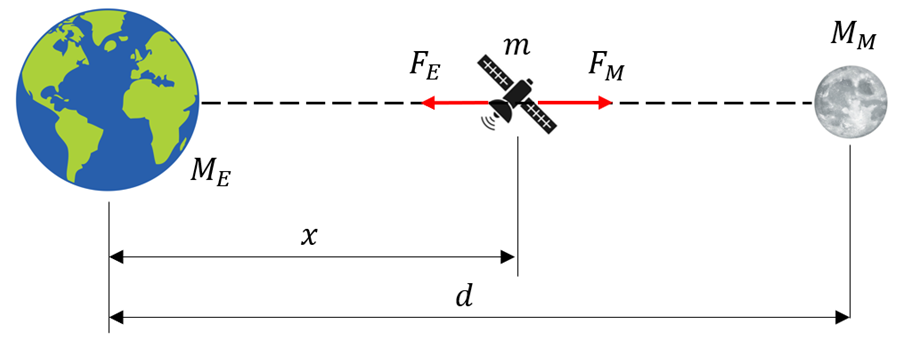
Lösung:
Sei d die Entfernung Erde-Mond und v die Entfernung vom Raumfahrzeug zum Mond. Die Gravitationskraft auf das Schiff der Masse m ist:
Die physikalische Lösung für
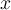 zwischen
zwischen 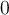 und
und 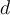 ist:
ist:Die Position beträgt
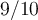 der Entfernung vom Mond und ist unabhängig von der Masse des Raumfahrzeugs.
der Entfernung vom Mond und ist unabhängig von der Masse des Raumfahrzeugs.2) Ein gleichförmiger Stab der Masse
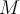 ist bereits zu einem Halbkreis mit Radius
ist bereits zu einem Halbkreis mit Radius 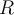 gebogen. Berechnen Sie die Kraft, die auf ein im Krümmungsmittelpunkt des Stabes befindliches Teilchen der Masse
gebogen. Berechnen Sie die Kraft, die auf ein im Krümmungsmittelpunkt des Stabes befindliches Teilchen der Masse 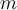 ausgeübt wird.
ausgeübt wird.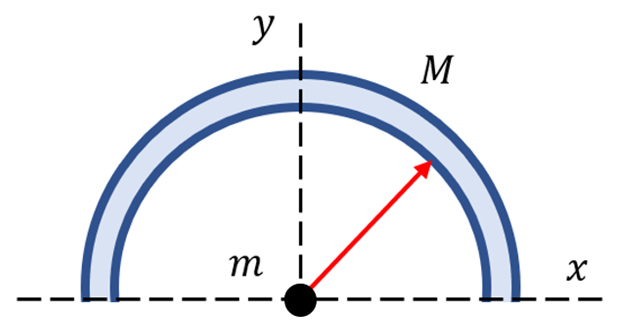
Lösung:
Wir teilen den Stab in Segmente der Bogenlänge
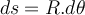 , deren Elementarmasse ist:
, deren Elementarmasse ist:Dieses Element übt in radialer Richtung eine Kraft
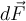 auf m links aus. Die horizontale Komponente
auf m links aus. Die horizontale Komponente 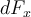 ergibt Null, wenn sie zu der des symmetrischen Elements addiert wird. Die vertikale Komponente
ergibt Null, wenn sie zu der des symmetrischen Elements addiert wird. Die vertikale Komponente 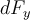 ist:
ist:Durch Integration über den gesamten Bogen erhalten wir die Gesamtkraft:
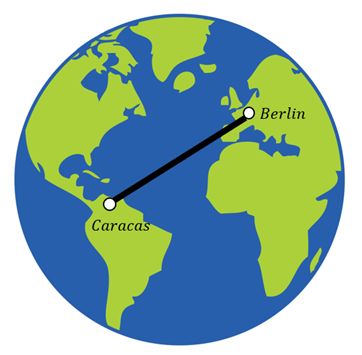
3) Es wurde vorgeschlagen, einen geraden Tunnel zu graben, der die Erde entlang eines Seils durchquert, das zwei Städte verbindet, um einen Zug zu bewegen, der keinen Antriebsmechanismus benötigt.
a) Nehmen Sie an, dass die Erde homogen wäre und ignorieren Sie die Reibung. Zeigen Sie, dass, wenn ein Objekt durch den Tunnel fallen gelassen wird, seine Bewegung vom einfachen harmonischen Typ wäre.
b) Finden Sie die Reisezeit zwischen den beiden Städten und zeigen Sie, dass sie nicht von der Länge des Tunnels oder der Masse des Objekts abhängt.
Lösung:
Befindet sich das Objekt in einem Abstand
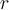 vom Erdmittelpunkt, hat die äußere Kugelschale keine Wirkung und die Gravitationskraft auf
vom Erdmittelpunkt, hat die äußere Kugelschale keine Wirkung und die Gravitationskraft auf 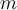 beruht ausschließlich auf der Masse
beruht ausschließlich auf der Masse 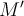 , die in der inneren Kugel mit dem Radius
, die in der inneren Kugel mit dem Radius 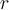 enthalten ist:
enthalten ist: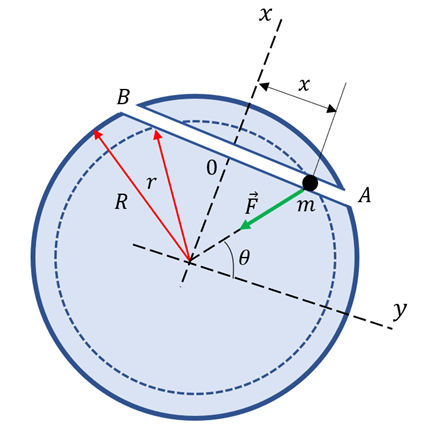
Die auf das Objekt ausgeübte Kraft wirkt zum Erdmittelpunkt hin:
Die
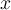 -Komponente dieser Kraft ist:
-Komponente dieser Kraft ist:Wenden wir Newtons 2. Gesetz an:
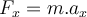 , haben wir:
, haben wir:Diese Differentialgleichung ist charakteristisch für einfache harmonische Bewegungen
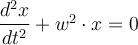 , wobei die Größe
, wobei die Größe 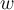 die Winkelgeschwindigkeit ist:
die Winkelgeschwindigkeit ist:b) Die Reisezeit beträgt die Hälfte des Zeitraums:
a) Es ist eine einfache harmonische Bewegung der Periode:
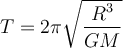
b)
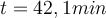 . Es kommt nicht auf die Länge des Tunnels oder auf die Masse an.
. Es kommt nicht auf die Länge des Tunnels oder auf die Masse an.

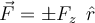
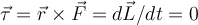
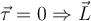
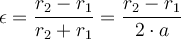
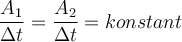
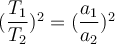
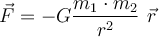
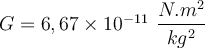
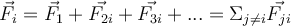
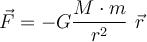

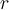

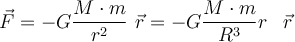
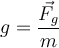
![[N/kg] [N/kg]](https://moodle.thga.de/filter/tex/pix.php/3bfba97f1ce3595a74c721e20e3d6e7d.png)
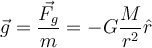
![\vec{W}=m.\vec{g} \hspace{2mm} [N] \vec{W}=m.\vec{g} \hspace{2mm} [N]](https://moodle.thga.de/filter/tex/pix.php/4d91db62df652e4d5a959485ca86e886.png)
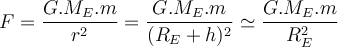
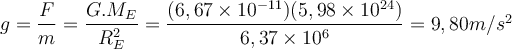
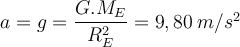
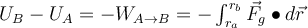
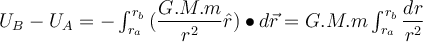
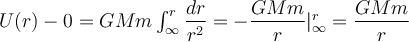
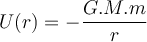
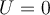
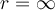
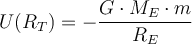
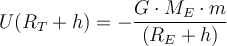
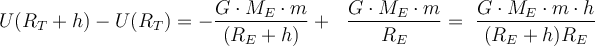
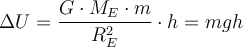
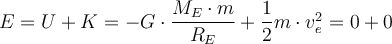
![v_e= \sqrt[]{\dfrac{2G \cdot M_E}{R_E}}= \sqrt[]{\dfrac{2 (6,67 \times 10^{-11} )(5,98 \times 10^{24} )}{6,37 \times 10^6 }}=11,2 \hspace{2mm}km/s v_e= \sqrt[]{\dfrac{2G \cdot M_E}{R_E}}= \sqrt[]{\dfrac{2 (6,67 \times 10^{-11} )(5,98 \times 10^{24} )}{6,37 \times 10^6 }}=11,2 \hspace{2mm}km/s](https://moodle.thga.de/filter/tex/pix.php/814762d39271ef5a8d1d54c998753bcb.png)
![v_e= \sqrt[]{\dfrac{2G \cdot M_E}{R_E}}=11,2 \hspace{2mm}km/s v_e= \sqrt[]{\dfrac{2G \cdot M_E}{R_E}}=11,2 \hspace{2mm}km/s](https://moodle.thga.de/filter/tex/pix.php/1df259e9df4b8ec61ddb77c0ba34092c.png)
![F_{ges}=F_M-F_E=G.m.[ \dfrac{M_E}{x^2} – \dfrac{ M_M}{(d-x)^2}]=0 F_{ges}=F_M-F_E=G.m.[ \dfrac{M_E}{x^2} – \dfrac{ M_M}{(d-x)^2}]=0](https://moodle.thga.de/filter/tex/pix.php/6776b0626d1131ad5be5f1ff75f8ed3b.png)
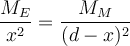
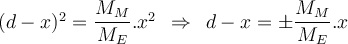
![x= \dfrac{d}{(1+ \sqrt[]{ \dfrac{M_M}{M_E}} )} = \dfrac{d}{ (1+ \sqrt[]{\dfrac{7,35\times10^{22}}{5,98\times10^{24}}})}= 0,90.d x= \dfrac{d}{(1+ \sqrt[]{ \dfrac{M_M}{M_E}} )} = \dfrac{d}{ (1+ \sqrt[]{\dfrac{7,35\times10^{22}}{5,98\times10^{24}}})}= 0,90.d](https://moodle.thga.de/filter/tex/pix.php/3eed45d9df5ac90dbf48a1b3e4f08105.png)
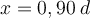
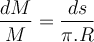

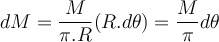
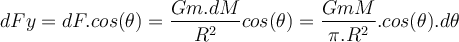
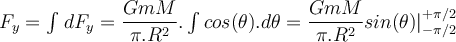
![F_y= \dfrac{ GmM}{ \pi.R^2} [(1)-(-1)]= 2\dfrac{ GmM}{\pi.R^2 } F_y= \dfrac{ GmM}{ \pi.R^2} [(1)-(-1)]= 2\dfrac{ GmM}{\pi.R^2 }](https://moodle.thga.de/filter/tex/pix.php/e1bb0b759370cc5dedcbb6a569b028fd.png)
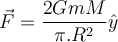
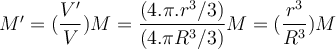
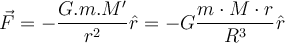
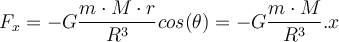
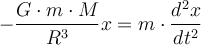

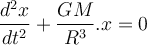
![w= \dfrac{ 2 \cdot \pi}{T} = \sqrt[]{ \dfrac{G \cdot M}{R^3} } w= \dfrac{ 2 \cdot \pi}{T} = \sqrt[]{ \dfrac{G \cdot M}{R^3} }](https://moodle.thga.de/filter/tex/pix.php/c1e38c78d694b944953d94c804f7dd76.png)