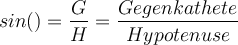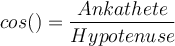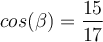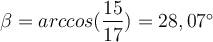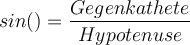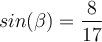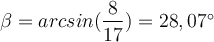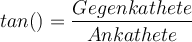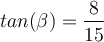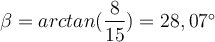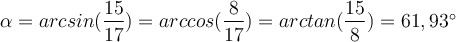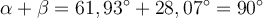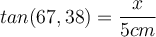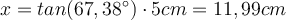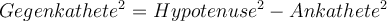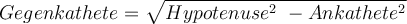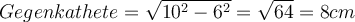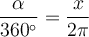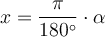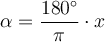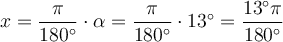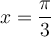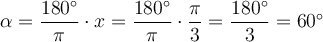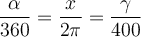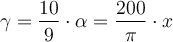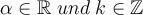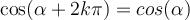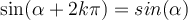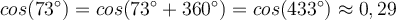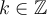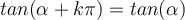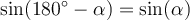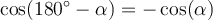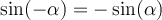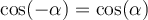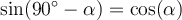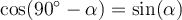Trigonometrische Funktionen
Abschnittsübersicht
-
-
Rechtwinkliges Dreieck
In dieser Lerneinheit zeige ich dir, wie du Sinus, Cosinus und Tangens anwenden kannst, um Winkelgrößen und Seitenlängen an einem rechtwinkligen Dreieck zu berechnen. 🧐Die folgende Abbildung stellt ein rechtwinkliges Dreieck mit den Seiten AB,AC und BC, die jeweils a, b und c lang sind, und den Winkeln α (ausgesprochen: Alpha) und ß (ausgesprochen: Beta) dar.
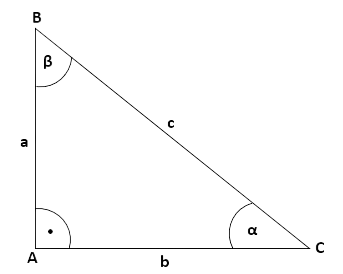
Rechtwinkliges Dreieck von O. Ibn Bevor wir direkt mit der Berechnung der Winkelgrößen oder Seitenlängen loslegen, ist es vorab einmal wichtig, die Katheten des Dreiecks zu bestimmen. Wie das geht, zeige ich dir. 👊Dabei musst du dich erstmal für einen Winkel entscheiden. Je nach gewähltem Winkel ändern sich die dazu gehörigen Ankathete und Gegenkathete. Die Hypotenuse ist im Gegensatz immer die längste Seite und liegt gegenüber dem rechten Winkel. 🤓In unserem Beispiel entscheiden wir uns für den Winkel α.
So ist die Ankathete, die Seite die sich neben dem Winkel befindet, also AC und die Gegenkathete, die Seite die sich gegenüber dem Winkel befindet, also AB.
Rechtwinkliges Dreieck mit Beschriftung (V1) von O. Ibn
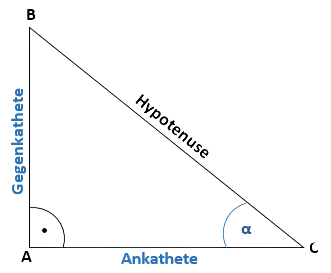
Als zweites Beispiel wählen wir den Winkel β aus.
Dabei sind die Ankathete AB und die Gegenkathete AC.
Rechtwinkliges Dreieck mit Beschriftung (V2) von O. Ibn
Gut, aber wie lassen sich nun die Größe eines Winkels oder die Länge einer Seite berechnen? 🙄Mit den drei trigonometrischen Funktionen Cosinus, Sinus und Tangens, werden Zusammenhänge zwischen Winkelgrößen und Seitenlängen formuliert.Und so sehen die Formeln aus: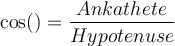
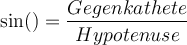
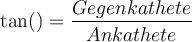
Bezogen auf dem Winkel αsind die Formeln also: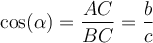
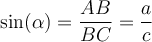
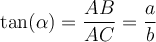
Und zum Winkel ß: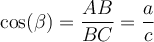
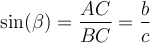
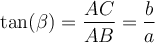
Tipp: Bei der Anwendung der trigonometrischen Funktionen kannst du dir die folgende Eselsbrücke merken: GAGA HüHnerhof AG.
Die Formeln ergeben sich, wenn die Großbuchstaben untereinander geschrieben werden: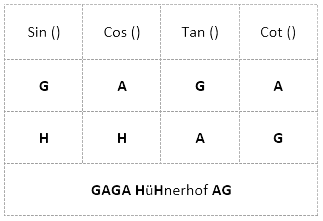
GAGA Hühnerhof AG von O. Ibn
Als Nächstes, erkläre ich dir, wie du die trigonometrischen Funktionen konkret einsetzen kannst anhand folgender Rechenbeispiele.Rechenbeispiel 1: Berechnung eines Winkels
Gegeben ist:
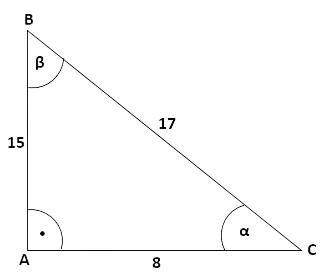
Abbildung zu Rechenbeispiel 1 von O. Ibn
Frage: Wie groß ist der Winkel ß?
Da alle Dreiecksseiten gegeben sind, können wir den Winkel ß mit allen drei trigonometrischen Funktionen berechnen. Mit wenigeren Angaben musst du dir aber darüber Gedanken machen, welche Formel am besten passt. 😉Lösung 1:
In unserem Beispiel heißt das:
Durch den Einsatz der Umkehrfunktion Arkuscosinus oder kurz arccos können wir den Winkel ß berechnen:
Lösung 2:
In unserem Beispiel heißt das:
Durch den Einsatz der Umkehrfunktion Arkussinus oder kurz arcsin können wir den Winkel ß berechnen:
Lösung 3:
In unserem Beispiel lautet das:
Durch den Einsatz der Umkehrfunktion Arkustangens oder kurz arctan können wir den Winkel ß berechnen:
Analog dazu lässt sich der Winkel α genauso berechnen:Frage: Wie groß ist der Winkel α ?
Lösung:
Wie kannst du jetzt prüfen, ob die berechneten Winkelgrößen richtig sind? 🤔Bei einem Dreieck, beträgt die Summe der drei Winkel 180°. Bei einem rechtwinkligen Dreieck ist die Größe des rechten Winkels schon bekannt, also 90°. Die Summe der zwei anderen Winkel sollte also 90° sein.In unserem Beispiel:
Rechenbeispiel 2: Berechnung einer Seitenlänge
Gegeben ist:

Abbildung zu Rechenbeispiel 2 von O. Ibn
Frage: Wie lang ist die Seite x?
Lösung:
Zuerst solltest du die richtige Formel aussuchen.
In unserem Beispiel entscheiden wir uns für die Tangensformel, wo die Ankathete und Gegenkathete zum Winkel α vorkommen.
So sieht dann der Lösungsweg aus:
Zur Berechnung der Seitenlängen bei einem rechtwinkligen Dreieck, kannst du den Satz des Pythagoras auch anwenden.Die Formel dazu lautet:
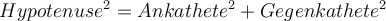
Rechenbeispiel:
Gegeben ist ein rechtwinkliges Dreieck mit einer Ankathete von 6 cm und einer Hypotenuse von 10 cm.
Frage: Wie lang ist die Gegenkathete ?
Lösung:
Der Satz des Pythagoras lautet: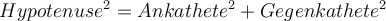
Rechnerisch umgesetzt ergibt dies:
Achte bei deinen Berechnungen auf folgenden Punkte 🤙- Die Seitenlängen müssen die gleiche Einheit haben, also zum Beispiel alles in Meter oder Zentimeter.
- Der Taschenrechner muss auf DEG für Degree eingestellt sein.
- Die Winkelgrößen werden durch den Einsatz von arccos, arcsin oder arctan berechnet.
-
Einheitskreis
Jeder Winkel im Einheitskreis lässt sich durch die Länge des Kreisbogens beschreiben. Die entsprechende Einheit ist das Bogenmaß. 🤓Veranschaulichung vin Gradmaß und Bogenmaß von O. Ibn
Dabei entspricht der volle Kreis einen Winkel von 360° in Gradmaß oder
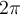 in Bogenmaß.
in Bogenmaß. Daraus lässt sich die Verhältnisgleichung aufstellen:
Ist der Winkel
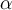 in Gradmaß angegeben und der entsprechende Wert
in Gradmaß angegeben und der entsprechende Wert 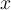 in Bogenmaß gesucht, so lässt sich die obige Gleichung nach
in Bogenmaß gesucht, so lässt sich die obige Gleichung nach 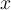 auflösen und wir erhalten:
auflösen und wir erhalten: Ist der Winkel
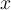 in Bogenmaß angegeben und der entsprechende Wert
in Bogenmaß angegeben und der entsprechende Wert 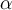 in Gradmaß gesucht, sieht die Gleichung dann so aus:
in Gradmaß gesucht, sieht die Gleichung dann so aus: Rechenbeispiel 1:
Gegeben ist α = 13°.
Gesucht ist die Winkelgröße
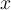 in Bogenmaß.
in Bogenmaß. Lösung:
Die Winkelgröße
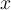 in Bogenmaß lässt sich berechnen, indem wir den Winkel α im Gradmaß in der entsprechenden Formel einsetzen.
in Bogenmaß lässt sich berechnen, indem wir den Winkel α im Gradmaß in der entsprechenden Formel einsetzen.Rechnerisch umgesetzt sieht es dann so aus:
Rechenbeispiel 2:
Gesucht ist der entsprechende Winkel α in Gradmaß.
Lösung:
Ähnlich wie beim ersten Beispiel, lässt sich die Winkelgröße α im Gradmaß berechnen, indem wir den Winkel
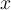 in Bogenmaß in der entsprechenden Formel einsetzen.
in Bogenmaß in der entsprechenden Formel einsetzen.Rechnerisch umgesetzt sieht es dann so aus:
Der nachfolgende Link führt zu einer externen Internetseite, die ggf. andere Datenschutzvorgaben erfüllt als wir es auf dieser Plattform tun. Dabei können Daten von dir übertragen und weiterverarbeitet werden. Wenn du dich allgemein zum Thema Datenschutz erkundigen möchtest, empfehlen wir dir die Erklärvideos der Initiative Datenschutz geht zur Schule.Im Vermessungswesen werden Winkelgrößen oftmals in Gon angegeben. Dabei entsprechen 400 Gon einen vollen Kreis, also 360° oder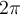 . 😲
. 😲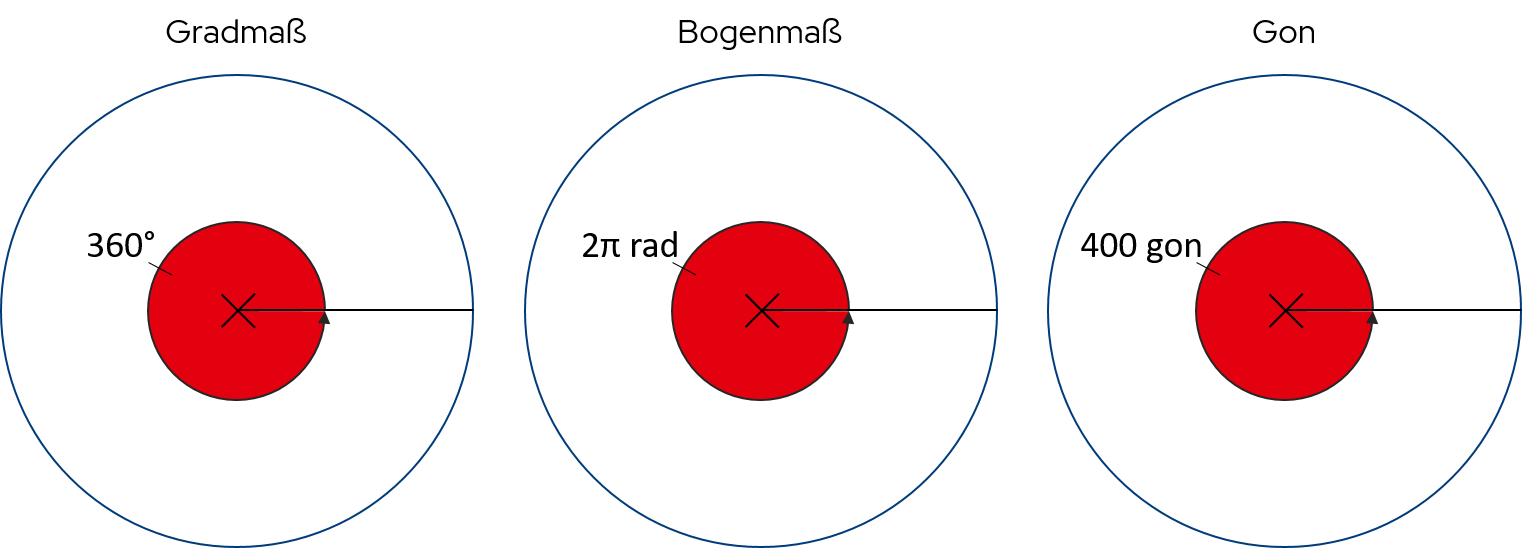
Gradmaß, Bogenmaß und Gon bei einer gleichförmigen Kreisbewegung von O. Ibn
Indem die Verhältnisgleichung erweitert wird, lassen sich nun Winkelgrößen in Gradmaß, Bogenmaß oder Gon umrechnen:
Ist der Winkel
 in Gon gesucht, so lässt sich die Verhältnisgleichung nach dem Winkel
in Gon gesucht, so lässt sich die Verhältnisgleichung nach dem Winkel  auflösen:
auflösen: Rechenbeispiel 3:
Frage:
Wie lassen sich 150° in Gon umrechnen?
Lösung:
Um die umgerechnete Winkelgröße zu erhalten, wird der Wert in Gradmaß α = 150° in der entsprechenden Formel eingesetzt.
Wir erhalten dann:
Lassen sich die Sinus-, Cosinus und Tangenswerte eines Winkels geometrisch definieren? 🤔Der nachfolgende Link führt zu einer externen Internetseite, die ggf. andere Datenschutzvorgaben erfüllt als wir es auf dieser Plattform tun. Dabei können Daten von dir übertragen und weiterverarbeitet werden. Wenn du dich allgemein zum Thema Datenschutz erkundigen möchtest, empfehlen wir dir die Erklärvideos der Initiative Datenschutz geht zur Schule.
Die Antwort ist ja. In diesem Video erfährst du wie man Cosinus-, Sinus- und Tangenswerte am Einheitskreis richtig ablesen kann. 🤓Je nach gewähltem Winkel erhältst du auch negative Sinus- und Cosinuswerte. Hier ist eine Übersicht mit den vier Quadranten und positiven oder negativen Wertebereichen:
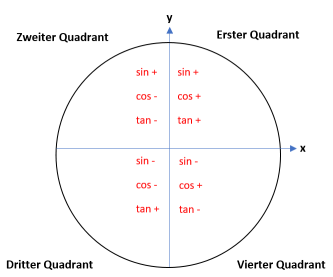
Quadranten und Wertebereiche am Einheitskreis von O. Ibn
In der folgenden Tabelle siehst du ein paar Winkelgrößen in Gradmaß und Bogenmaß und deren entsprechenden Sinus-, Cosinus- und Tangenswerten. 😉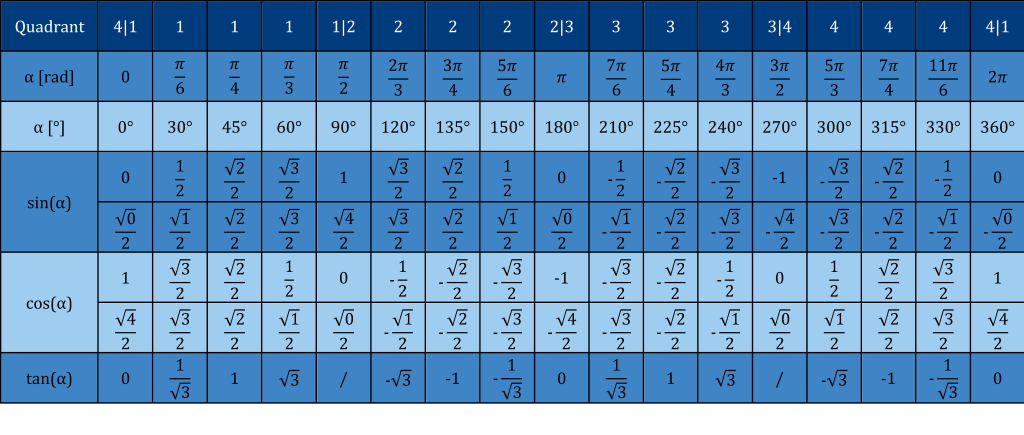
Winkeltabelle von N. Donner
Zudem gelten für die Cosinus-, Sinus- und Tangensfunktionen folgende Regeln. 👊1) Periodizität:
Die Cosinus- und Sinusfunktionen sind 360° oder
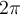 periodisch.Man erhält also die gleichen Sinus- bzw. Cosinuswerte, wenn man den Winkel um ein beliebiges ganzzahliges Vielfaches von
periodisch.Man erhält also die gleichen Sinus- bzw. Cosinuswerte, wenn man den Winkel um ein beliebiges ganzzahliges Vielfaches von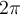 (im oder gegen den Uhrzeigersinn) dreht.
(im oder gegen den Uhrzeigersinn) dreht.Beispiel:
Ähnlich wie bei der Sinus- und Cosinusfunktion, ist die Tangensfunktion
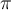 periodisch.
periodisch. 2) Supplementbeziehungen
Winkel, die sich zu 180° summieren, nennt man Supplementwinkel. Es gelten hier die Supplementbeziehungen:
Daraus lässt sich feststellen, dass zu jedem Sinuswert außer -1 und 1 gibt es zwei Winkel aus [0°,360°[, nämlich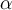 und
und 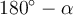 .
.Beispiel:
Abbildung zu Supplementbeziehungen von O. Ibn
3) Negative Winkelmaße
Für negative Winkelmaße gilt:
Daraus lässt sich feststellen, dass zu jedem Cosinuswert außer 1 und -1 gibt es zwei Winkel aus [0°,360°[, nämlich und
und  .
.Beispiel:
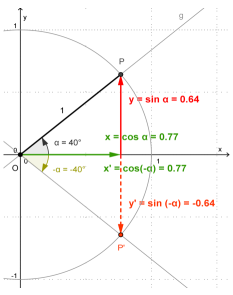
Abbildung zu negativen Winkelmaßen von O. Ibn
4) Komplementbeziehungen
Winkel, die sich zu 90° summieren, nennt man Komplementwinkel. Es gelten hier die Komplementbeziehungen:
5) Goniometrische Grundformel
Nach dem Satz des Pythagoras gilt: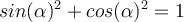
Beispiel:
cos(60°)2 + sin(60°)2 = 1
Abbildung zur goniometrischen Grundformel von O. Ibn
Wichtig dabei ist zu beachten dass:
- Sinus und Cosinus für alle Winkel definiert sind. Ihre Werte liegen im Bereich [-1;+1].
- der Tangens für die Winkel 90°, 270° ... nicht definiert ist , da die Ankathete an diesen Stellen gleich 0 ist. Bsp: tan(90°) = GK/0 = nicht definiert.
- der Taschenrechner richtig eingestellt ist. Dabei steht "Deg" für Gradmaß, "Rad" für Bogenmaß und "Gra" für Gon.
-
Exkurs : Trigonometrie in der Vermessungskunde
Dieser Exkurs bietet euch ein Praxisbeispiel zur trigonometrischen Höhenmessung.In der Geodäsie, insbesondere im Vermessungswesen finden u.a. trigonometrische Funktionen praktische Anwendung. Dabei werden die Koordinaten (Lage und Höhe) von bestimmten Gelände- (Bergspitzen, Flüsse, Straßen, etc.) oder Gebäudepunkten bzw. deren Entfernung zueinander ermittelt.
Der nachfolgende Link führt zu einer externen Internetseite, die ggf. andere Datenschutzvorgaben erfüllt als wir es auf dieser Plattform tun. Dabei können Daten von dir übertragen und weiterverarbeitet werden. Wenn du dich allgemein zum Thema Datenschutz erkundigen möchtest, empfehlen wir dir die Erklärvideos der Initiative Datenschutz geht zur Schule.Im Bachelorstudiengang Vermessungswesen oder auch im Masterstudiengang Geoingenieurwesen und Nachbergbau kannst du lernen, wie das genau funktioniert. 💡Vermessungsingenieurinnen und -ingenieure erfassen Geodaten mithilfe modernster Technik. Dazu gehören beispielsweise elektronische Tachymeter, hochgenaue Satellitenempfänger (GNNS), photogrammetrische Verfahren, Laserscanner und Nivelliergeräte. Die Messdaten werden softwaregestützt ausgewertet und mit Hilfe von Geoinformationssystemen und Web-Diensten dokumentiert und visualisiert.⬇⬇⬇ Im Folgenden schauen wir uns gemeinsam an, wie die Höhenbestimmung mit einem Tachymeter funktioniert. ⬇⬇⬇Höhenbestimmung mit dem Tachymeter
Im Vermessungswesen werden für die trigonometrische Höhenbestimmung unter anderem sogenannte Tachymeter eingesetzt. In der nachfolgenden Slideshow bekommst du einen ersten Eindruck, wie ein Tachymeter aussieht:
Tachymeter im Einsatz von L. Cebula und L. Michael.
Der Begriff Tachymeter setzt sich aus den griechischen Wörtern für schnell (tachys) und Maß (metron) zusammen. Schnell hört sich doch schon mal gut an! Aber was genau kann das Tachymeter denn eigentlich?Mit einem Tachymeter lässt sich der Zenitwinkel, also der Winkel eines Punktes unter dem Zenit bestimmen. Das Gerät kann außerdem die Horizontalrichtung über den Horizontalwinkel und die Schrägdistanz zu einem bestimmten Geländepunkt messen. Hierfür wird ein Reflektor notwendig, da die Schrägdistanz über die doppelte Laufzeit eines Laserimpulses (Hin- und Rückweg) gemessen wird.
Zenitwinkel, Horizontalrichtung, Horizontalwinkel und Schrägdistanz - hast du diese Begriffe schon mal gehört. ❓
Wenn du die Begriffe schon kennst, dann überspringe den nächsten Abschnitt sieh dir direkt das darauffolgende Bild an. ⏭
Wenn du die Begriffe noch einmal nachlesen willst, dann solltest du dir nachfolgend das Zusatzwissen ansehen. 🧐Zenitwinkel: Der Zenitwinkel ist der Winkel eines Punktes unter dem Zenit. Der Zenit wiederum ist die nach oben verlängerte Lotrichtung eines Standortes.Um das ganze weniger abstrakt zu machen, stell dir folgendes vor: Du stehst auf einer ebenen Fläche, deine Füße sind geschlossen und deine Arme liegen am Körper an, so dass die Fingerspitzen zum Boden zeigen. Wenn du jetzt deinen Kopf bewegst und über dir in den Himmel guckst, dann guckst du in den Zenit - die Blickrichtung entspricht der Vertikalebene.Auf dem nachfolgenden Bild gehen wir natürlich nicht von der Position der Person sondern von der Position des Tachymeters aus. Und da das Tachymeter nicht nach oben blicken kann, sprechen wir hier auch nicht von der Blickrichtung, sondern von der Stehachse des Gerätes.Nun kehren wir wieder zu der Vorstellung zurück, dass du auf einer ebenen Fläche an der frischen Luft stehst und immer noch über dir in den Himmel guckst (gibt es dort eigentlich etwas Interessantes zu entdecken? 🛫 🪂). Strecke nun einen Arm auf Schulterhöheseitlich von dir aus und zeige mit dem Zeigefinger auf ein Objekt, dass sich in der Richtung befindet. Der Zenitwinlel ist nun der Winkel zwischen deiner Blickrichtung und der Fingerspitze deines Zeigefingers 👉 Wenn dein ausgestreckter Arm einen rechten Winkel mit deinem Oberkörper bildet, dann würde der Zenitwinkel 90 Grad (oder auf vermesserisch 100 Gon) betragen. 📐Auf dem untenstehenden Bild gehen wir wieder von der Position des Tachymeters aus. Der Zenitwinkel wird hier durch die Stehachse des Gerätes und der Schrägdistanz gebildet.Die Schrägdistanz ist übrigens die direkt gemessene Distanz zwischen dem Tachymeter und unserem Zielpunkt, dem Reflektor.Horizontalrichtung: Die Horizontalrichtung ist eine nicht orientierte Richtung in der Horizontalebene.Warum nicht orientiert? 🤔In dem nachfolgenden Bild ist die Horizontalrichtung die projizierte Gerade, die vom Reflektor zurückgeworfen wird.
Um das zu erklären, schauen wir uns zuerst noch einmal das Gegenstück, die Vertikaleben an. Die Vertikaleben ist durch den Zenit und seinen Gegenpol, den Nadir - also die Verlängerung der Lotrichtung nach unten - bestimmt. Für die Vertikalebene haben wir also eine eindeutige 0-Richtung. Die Horizontalrichtung dagegen hat keine eindeutige 0-Richtung, sondern ist eine auf einer horizontalen Ebene projizierte Raumgerade.
Horizontalwinkel: Der Horizontalwinkel ergibt sich aus der Differenz zweier Horizontalrichtungen. Im nachfolgenden Bild also durch die als Horizontalrichtung beschrieben Gerade und die als Nullrichtung beschriebene Gerade.Die Nullrichtung ist diejenige Horizontalrichtung, auf welche die übrigen Richtungen bezogen werden. Somit wird der Horizontalwinkel zwischen der Nullrichtung einer weiteren Horizontalrichtung bestimmt.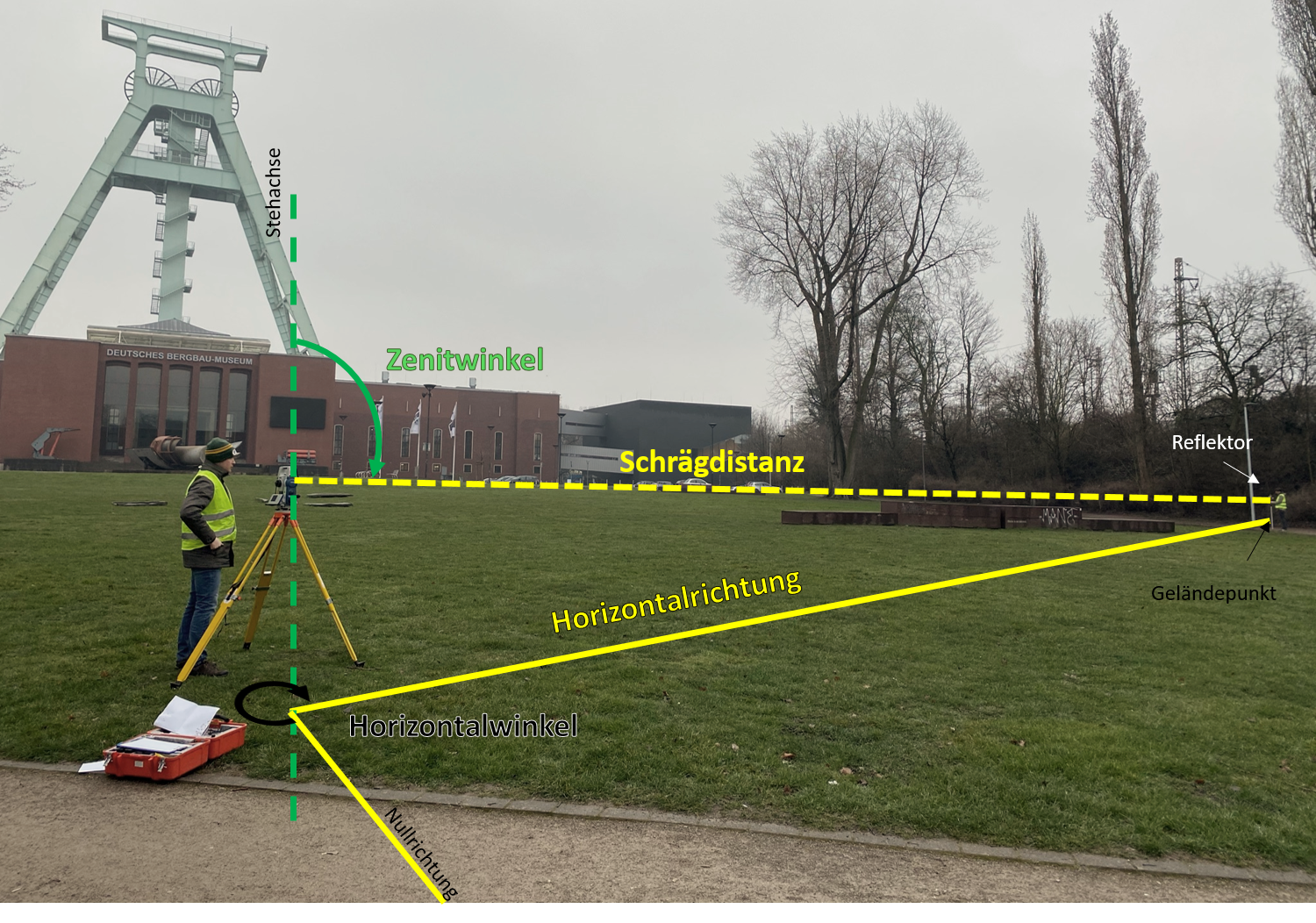
Vermerssung mit dem Tachymeter von L. Cebula.
Turmhöhenbestimmung mit dem Tachymeter in der Praxis
Die vorrangige Aufgabe bei der Turmhöhenbestimmung besteht in der Ermittlung der Distanz zwischen Instrument und Zielpunkt. Ist der Zielpunkt nicht zugänglich, kann über bestimmte Messkonstellationen von Winkeln und Strecken der Höhenunterschied zum Zielpunkt trigonometrisch berechnet werden. Die bekanntesten Messkonstellationen bezeichnet man als Messung mit einem horizontalen (bzw. vertikalen) Hilfsdreieck 📐
Der nachfolgende Link führt zu einer externen Internetseite, die ggf. andere Datenschutzvorgaben erfüllt als wir es auf dieser Plattform tun. Dabei können Daten von dir übertragen und weiterverarbeitet werden. Wenn du dich allgemein zum Thema Datenschutz erkundigen möchtest, empfehlen wir dir die Erklärvideos der Initiative Datenschutz geht zur Schule.Wenn du dir das obenstehende Bild aufmerksam angeguckt hast, hast du vielleicht erkannt was wir nun vermessen werden ⁉️
Es ist das Fördergerüst des Deutschen Bergbau-Museum Bochum ‼️
Solltest du das Museum einmal besuchen, so wirst du feststellen dass du mit einem Fahrstuhl sogar auf das Fördergerüst hinaufgelangen und die Aussichtsplattform besuchen kannst. Wenn wir zurück zu unserer Vermessungsaufgabe kommen, müssen wir jedoch feststellen, dass unser Zielpunkt noch ein Stück über der Plattform liegt, der höchste Punkt ist die Antenne – das kannst du gut erkennen, wenn du unserem Vermessungsingenieur auf dem nächsten Bild über die Schulter blickst. 👀
Blick über die Schulter eines Vermessungsingenieurs von L. Cebula
Für die Turmhöhenbestimmung bedeutet dies, dass der Zielpunkt nicht zugänglich ist und wir daher mit einem Hilfsdreieck 📐 arbeiten um dem Höhenunterschied trigonometrisch zu berechnen. Und ebendieses Hilfsdreieck ist auf dem nächsten Bild abgebildet. Die Messung mit dem Tachymeter wird übrigens aus zwei verschiedenen Perspektiven durchgeführt, weswegen wir auf dem nachfolgenden Bild ein Tachymeter bei Standort A und ein Tachymeter bei Standort B sehen.
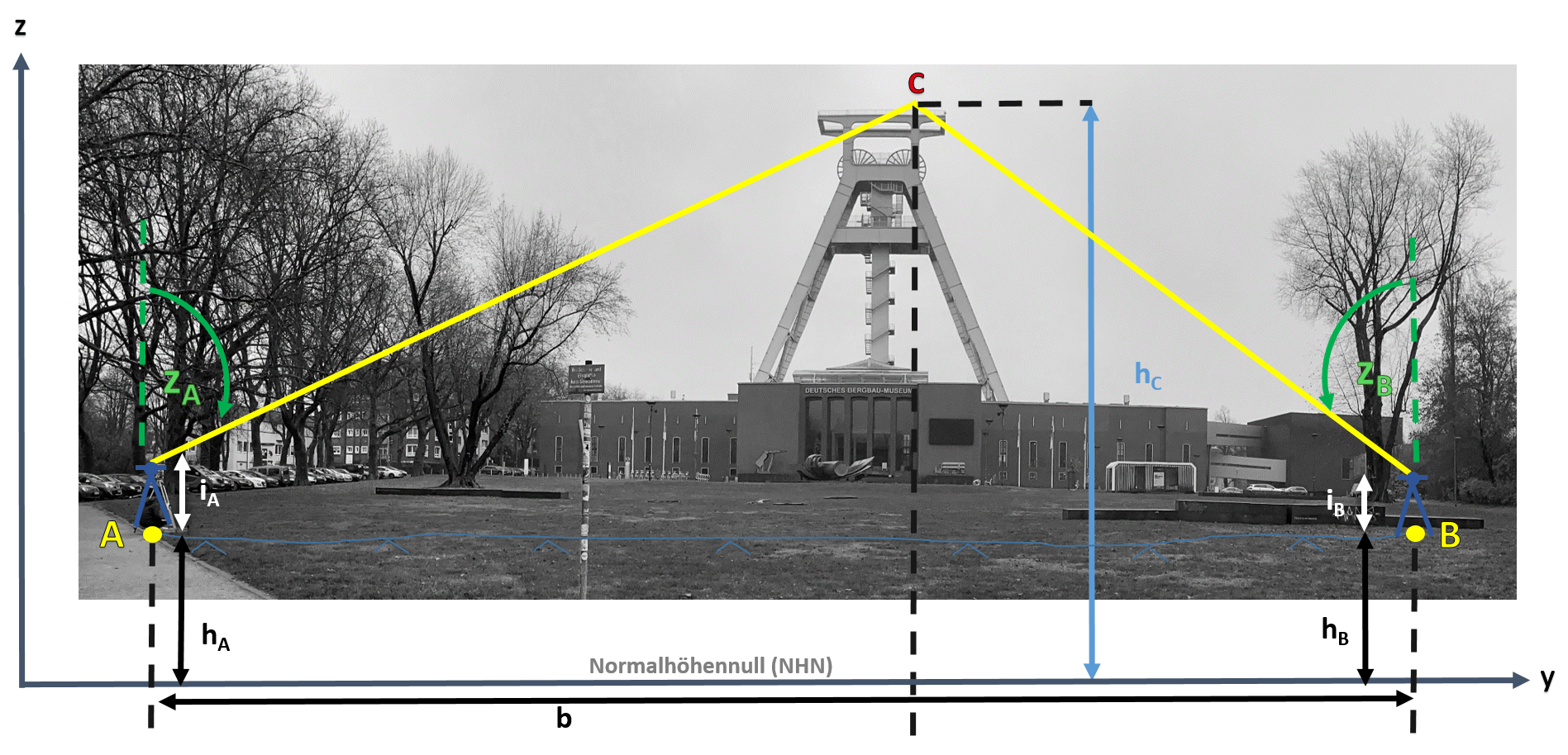
Hilfsdreieck zur trigonometrischen Höhenbestimmung von L. Cebula Der nachfolgende Link führt zu einer externen Internetseite, die ggf. andere Datenschutzvorgaben erfüllt als wir es auf dieser Plattform tun. Dabei können Daten von dir übertragen und weiterverarbeitet werden. Wenn du dich allgemein zum Thema Datenschutz erkundigen möchtest, empfehlen wir dir die Erklärvideos der Initiative Datenschutz geht zur Schule.Fassen wir einmal zusammen, was wir auf dem Bild erkennen können:
- Um das Bild herum wurde ein Koordinatensystem gelegt, in welchem die y-Achse die Breite und die z-Achse die Höhe darstellt
- Als Nullpunkt für unsere z-Achse gilt Normalhöhennull (NHN)
- Mithilfe der beiden Standorte des Messgerätes bzw. des Tachymeters (Punkt A und Punkt B) sowie der Spitze des Fördergerüsts (Punkt C) haben wir ein Hilfsdreieck gebildet (ABC)
- Für Standort A und Standort B haben wir jeweils die Zenitwinkel eingezeichnet (ZA und ZB)
- Für Standort A und Standort B haben wir jeweils die Instrumentenhöhen eingezeichnet (iA und i B)
- Für Standort A und Standort B haben wir jeweils die Punkthöhen hA und hb eingezeichnet, die angeben wie weit sich das Messgerät am jeweiligen Standort über NHN befindet
- Wir haben die gesuchte Höhe hc eingezeichnet
Was müssen wir nun noch beachten um die Turmhöhe zu bestimmen? Wir müssen die Höhe des Instrumentenhorizonts berücksichtigen und die Position des Gerätes im geodätischen Koordinatensystem bestimmen:
- Um die Höhe des Instrumentenhorizontes, also der Höhe der Kippachse des Fernrohrs über Normalhöhennull (NHN) in A und B zu bestimmen, werden die Punkthöhen hA und hB mittels Nivellement ermittelt und die Instrumentenhöhe iA bzw. iB dazu addiert.
- Um die gesuchte Höhe ermitteln zu können, muss die Position des Gerätes im geodätischen Koordinatensystem bestimmt werden. Hierfür werden die Richtungswinkel benötigt. Das sind Horizontalwinkel, die auf eine gemeinsame Nullrichtung bezogen werden. Wie wir weiter oben bereits erfahren haben, werden einfache Horizontalwinkel durch die Differenz zweier Richtungswinkel berechnet.
Die nach rechts gedrehten Richtungswinkel lassen sich am besten aus der Vogelperspektive betrachten und sind auf dem nachfolgenden Bild eingezeichnet:Richtungswinkel aus der Vogelperspektive von L. Cebula Wichtig ist außerdem zu wissen, dass die Winkel meistens in der geodätischen Winkeleinheit Gon ermittelt werden.Was es mit der Einheit Gon auf sich hat und in welchem Verhältnis Gradmaß, Bogenmaß und Gon zueinander stehen hast du in der vorhergehenden Lerneinheit zum "Einheitskreis" erfahren. Zur Erinnerung sei noch einmal kurz gesagt dass Gon es erlaubt, den vier Quadranten des Einheitskreises jeweils eine eigene Hunderter-Stelle zuzuordnen: 0°=0 gon, 90°=100 gon, 180°=200 gon, 270°=300 gon und 360°=400 gon.Die Angabe in gon vereinfacht die manuelle Einstellung von rechten Winkeln (100 gon bzw. 300 gon) und gestreckten Winkeln (200 gon). Letztere sind im Zusammenhang mit redundanten Präzisionsmessungen mit Theodoliten bzw. Tachymetern in zwei Fernrohrlagen von großer Bedeutung, weil grobe Messfehler bei der visuellen Teilkreisablesung von Horizontalkreis und Vertikalkreis einfach zu erkennen sind. Das liegt daran, dass die Differenzen der beiden jeweiligen Ablesungen 200 gon betragen müssen und sich daher nur in der Hunderterstelle unterscheiden dürfen.Zu beachten ist allgemein, dass das geodätische Koordinatensystem x- und y-Achse vertauscht, weil im mathematischen System der Richtungswinkel gegen den Uhrzeigersinn (und damit entgegen der Winkelmessrichtung der Vermessungsinstrumente) läuft und die Nullrichtung nicht nach Nord, sondern ostwärts zeigt. Um nicht für alle geodätischen Berechnungen Sonderformeln entwickeln zu müssen, hat man sich entschlossen, stattdessen nur die beiden Achsen zu tauschen. Dadurch können allgemeingültige, mathematische Formeln ohne Anpassung verwendet werden.Aufgabe:
Mit dem bisherigen Ablauf, dem Nivellement und den Messergebnissen des Tachymeters haben nun alle notwendigen Informationen zusammen um die Rechenaufgabe anzugehen und - endlich - die Turmhöhe zu bestimmen.
Dazu gibt es zunächst eine Übersicht über alle Werte, die wir bisher in Erfahrung bringen konnten:Instrumentenhöhen:- IA = 1,49 m
- IB = 1,63 m
Punkthöhen:- hA = 80,64 m
- hB = 80,99 m
- tA,C = 166,1104 g
- tA,B = 189,7312 g
- tB,C = 103,8011 g
- tB,A = 389,7312 g
Und nun zu unserer eigentlichen Rechenaufgabe:Hilfsdreieck zur Turmhöhenbestimmung von L. Cebula Gesucht werden:- Die Dreieckswinkel Alpha, Beta und Gamma
- Die Horizontalstrecken a und b
- Die relativen Höhenunterschiede hA,C und hB,C
- Die Absoluthöhe HC (sowohl von Punkt A als auch von Punkt B aus)
Bevor du mit dem Rechnen beginnst, empfehlen wir dir noch einmal das nachfolgende Video anzusehen, dass alle bisherigen Schritte der Turmhöhenmessung zusammenfasst. 🎥