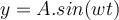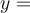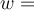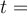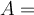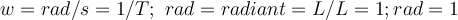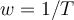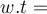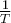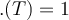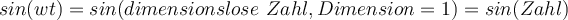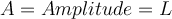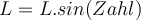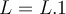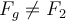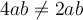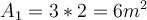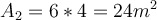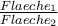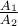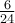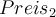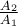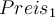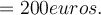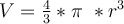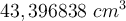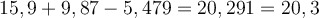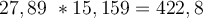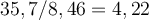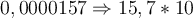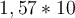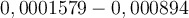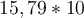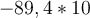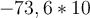Physikalische Größen & Einheiten
Abschnittsübersicht
-
Physikalische Gesetze drücken die Wechselwirkungen zwischen verschiedenen physikalischen Größen wie Länge, Kraft, Energie usw. in Form von Aussagen und mathematischen Gleichungen aus. Wie du diese Größen und die Ergebnisse in einer symbolischen Sprache (Einheitensystem) richtig schreibst und in Beziehung setzt, lernst du in diesem Modul.
Am Ende dieses Modul solltest du:
- die Physikalische Größen und die verschiedene Einheitensysteme kennen und verstehen.
- die richtige Anwendung der Dimensionsanalyse und Skalierungsgesetze verstehen und ausführen.
- die Grundbegriffe der wissenschaftliche Schreibweise, deren Bedeutung und Zusammenhänge kennen.
- die richtige Schreibweise der Ergebnisse physikalischer Berechnungen und die richtige Anzahl signifikanter Stellen verstehen und anwenden .
Da dieses Modul Grundlagen zu physikalischen Größen und Einheiten behandelt gibt es keine verschiedenen Level, wie du es vielleicht in anderen Modulen gesehen hast. Dennoch haben wir einen Eingangs- und einen Abschlusstest entworfen, damit du sehen kannst wie fit du vor und nach dem Durcharbeiten der Inhalte bist. 😉
Die Bearbeitungsdauer für alle Inhalte und Aufgaben schätzen wir auf maximal 60 Minuten. ⌛️ Dies hängt aber ganz stark davon ab wie viel Vorwissen du hast und ob du dir alle Inhalte anguckst. Wenn du nur einzelne Übungen oder sogar nur den Abschlusstest machst bist du natürlich viel schneller. 😋-
Einführung 📝
Physikalische Größen sind bestimmte Eigenschaften oder beobachtbare Aspekte eines physikalischen Systems, die in nummerischer Form ausgedrückt werden können. Die Größen sind messbar, wie zum Beispiel Masse, Energie oder Temperatur und werden durch Experimente bestimmt.
Fundamentale Größen
In der Physik beziehen sich sowohl Gesetze als auch Definitionen auf verschiedene mathematische Größen. In der Physik unterscheidet man zwischen fundamentalen Größen und abgeleiteten Größen. Fundamentale Größen in der Mechanik sind bspw. Länge, Zeit und Masse. Diese "Basisgrößen" sind Konzepte, die wir uns natürlich aneignen, indem wir Dinge wahrnehmen. Zum Beispiel nehmen wir auf dem Weg von zu Hause zur Schule, zur Hochschule oder zur Arbeit die Konzepte "Länge" und "Zeit" wahr, während wir unterwegs sind.
Es gibt verschiedene fundamentale Größen - eine komplette Liste dazu findest du unter der Abbildung. Momentan werden wir in unseren Übungen und in zukünftigen Modulen häufiger Masse, Zeit und Länge verwenden, die wie folgt definiert sind (es reicht wenn du die Konzepte kennst, du brauchst sie aber nicht auswendig zu lernen 😉):
- Länge ist ein Konzept, das direkt mit der Idee der Distanz oder der Ausdehnung von Körpern verbunden ist.
- Zeit ist ein Konzept, das mit dem Tag verbunden ist, an dem physikalische Ereignisse in geordneten Sequenzen auftreten und für ein bestimmtes Intervall andauern. Zeitintervalle sind durch einen Anfang und ein Ende bestimmt.
- Masse ist eine Eigenschaft jedes Körpers, die die Intensität seiner gravitativen Wechselwirkung mit anderen Körpern und auch seine Reaktion auf äußere Kräfte bestimmt.
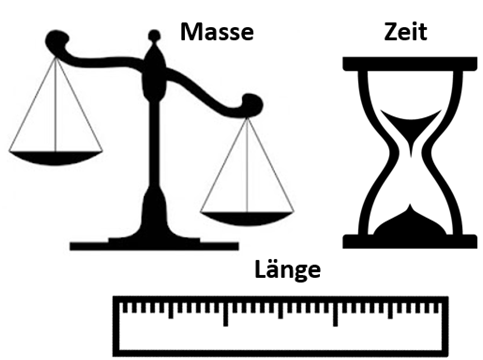
Fundamentale Größen. G. Jimenez Liste der Fundamentalgrößen:
- Länge
- Masse
- Zeit
- Temperatur
- Lichtstärke
- Stoffmenge
- Elektrischer Strom
-
Einheitensysteme
Physik hilft uns, Dinge zu messen und vorherzusagen. Mithilfe von Messungen kann die Welt auf systematische Weise beobachtet werden, um anschließend ein Modell zu erstellen und Vorhersagen treffen zu können. Um dies auszudrücken gibt es verschiedene Maßstäbe, zum Beispiel für Länge, Gewichte, Zeit und vieles mehr.
Der nachfolgende Link führt zu einer externen Internetseite, die ggf. andere Datenschutzvorgaben erfüllt als wir es auf dieser Plattform tun. Dabei können Daten von dir übertragen und weiterverarbeitet werden. Wenn du dich allgemein zum Thema Datenschutz erkundigen möchtest, empfehlen wir dir die Erklärvideos der Initiative Datenschutz geht zur Schule.Ein Messvorgang definiert eine physikalische Größe. Durch den Messvorgang bekommt man einen konkreten Wert und eine Einheit heraus, zum Beispiel kann man mit dem Lineal den Wert 12 mit der Einheit cm ausmessen. Für Messungen benötigt man ein Messgerät und eine Messskala. Im Alltag, in der Schule oder zu Hause könnten dies das Lineal oder der Gliedermaßstab (auch als Zollstock bekannt 😉) sein, die bereits in Zentimeter (cm) unterteilt sind. Vermessungsingenieurinnen und -ingenieure benutzen zum Beispiel elektronische Tachymeter oder Laserscanner und -tracker.
Internationales Einheitensystem
Die wissenschaftliche Gemeinschaft und viele andere Menschen müssen ihr Messsystem standardisieren, damit die von einigen gelieferten Daten von anderen interpretiert werden können und Messungen miteinander vergleichbar sind. Die Auswahl von Standard- oder Standardeinheiten bestimmt, welches Einheitensystem genutzt wird. Das in Europa gängigste System ist das SI-System (das steht für Systéme International d'Unitès) in der Variante des MKS-Systems (Meter-Kilogramm-Sekunde):
- Meter (m): ist die Entfernung, die Licht im Vakuum während eines Zeitintervalls von 1/299792458 Sekunden zurücklegt.
- Kilogramm (kg): ist die Masse eines zylindrischen und acizo-Prototyps aus einer Legierung aus Platin und Iridium (der im Internationalen Amt für Maß und Gewicht in Paris aufbewahrt wird).
- Sekunde (s): ist definiert als das 9.192.631.770-fache der Dauer einer Schwingung, die mit einem atomaren Übergang zwischen zwei Niveaus des Cäsium-133-Atoms verbunden ist.
In der folgenden Tabelle findest du eine Überblick über die Dimensionen und Einheiten der fundamentalen Größen des internationalen Einheitensystems (IS):
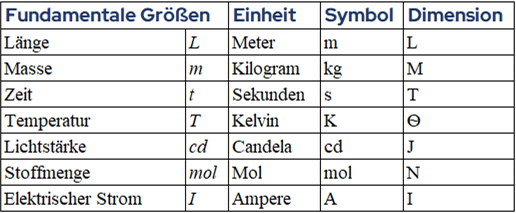
Tabelle des internationalen Einheitensystems. G. Jimenez Andere Einheitensysteme
Neben dem in Europa gängigen SI-System gibt es weitere Einheitensysteme, in welche du hier einen kurzen Einblick bekommst. Das eher selten anzutreffende, aber ebenfalls korrekte CGS-System (Zentimeter-Gramm-Sekunde) unterscheidet sich im Vergleich zum MKS-System in den Grundeinheiten für die Länge und die Masse. Auch die Engländer haben ihrerseits ihr eigenes Einheitensystem geschaffen, das als Angloamerikanisches Maßsystem bezeichnet wird, schließlich gibt es im Ingenieurwesen auch ein technisches Maßsystem. Im Allgemeinen gibt es viel mehr Einheitensysteme und wenn wir wollten, können wir selbst eines erstellen, aber es ist wichtig zu wissen, welche im Alltag und in der Technik am häufigsten verwendet werden.In der folgenden Tabelle findets du eine Übersicht zu den verschiedenen gängigsten Einheitensystemen:
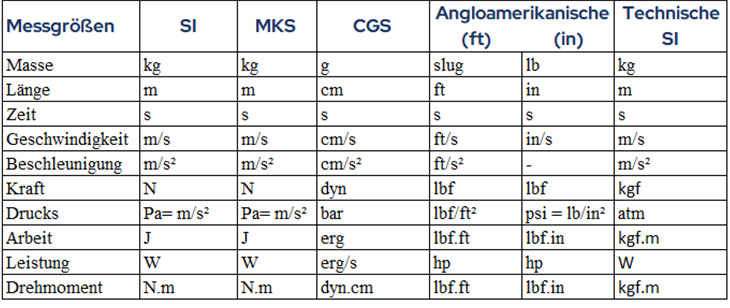
Tabelle des anderen Einheitensysteme. G.Jimenez Normalerweise wird es in der Praxis je nach Problemstellung, Arbeitsumgebung oder Kunde notwendig sein, das eine oder das andere System zu verwenden. Dies hilft uns, Einheiten zu vergleichen und sie von der physischen und akademischen Ebene auf eine für jeden verständlichere Ebene zu bringen. Vielleicht sind wir im Alltag auf einige physikalische Dilemmata gestoßen, die wir analysieren müssen, um das Problem besser zu verstehen.
Beispiel:Wir kaufen eine 2 Liter Flasche Wasser und möchten wissen, wie viel sie in wiegt. Wir haben die Flasche auf eine Waage gestellt und als Ergebnis werden uns 2 kg angezeigt. Das bedeutet, dass jeder Liter Wasser 1 kg wiegt. Nun möchten wir Ihr Gewicht in Pfund für unsere amerikanischen und englischen Freunde wissen. In diesem Fall verwenden wir eine englische Waage und als Ergebnis erhalten wir, dass jeder Liter 2,2 Pfund wiegt, d.h. jedes kg entspricht 2,2 Pfund.Es gibt auch einige praktische Zusammenhänge, die täglich für verschiedene Szenarien und für verschiedene Größenordnungen verwendet werden können. Physikalische Übungen sind in der Regel für diese Zusammenhänge konzipiert. Diese Zusammenhänge sind Teil des sogenannten Einheitenumrechnungssystems. Hier sind einige davon.
wiegt. Wir haben die Flasche auf eine Waage gestellt und als Ergebnis werden uns 2 kg angezeigt. Das bedeutet, dass jeder Liter Wasser 1 kg wiegt. Nun möchten wir Ihr Gewicht in Pfund für unsere amerikanischen und englischen Freunde wissen. In diesem Fall verwenden wir eine englische Waage und als Ergebnis erhalten wir, dass jeder Liter 2,2 Pfund wiegt, d.h. jedes kg entspricht 2,2 Pfund.Es gibt auch einige praktische Zusammenhänge, die täglich für verschiedene Szenarien und für verschiedene Größenordnungen verwendet werden können. Physikalische Übungen sind in der Regel für diese Zusammenhänge konzipiert. Diese Zusammenhänge sind Teil des sogenannten Einheitenumrechnungssystems. Hier sind einige davon.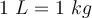 nur für Wasser
nur für Wasser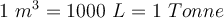
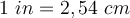
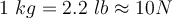
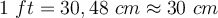
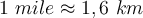 Beim Ausrechnen von z.B. Druck, ist es wichtig, dass du die Größen aus nur einem Maßsystem nutzt. Wenn du das nämlich nicht tust, bekommst du ein sinnloses Ergebnis verschiedener Einheiten. Also ist es wichtig, dass du die verschiedenen Systeme nicht durcheinander bringst.Hinweis: Bei den Berechnungen ist es wichtig, immer das gleiche Einheitensystem zu verwenden, da sonst die Ergebnisse nicht korrekt sind.
Beim Ausrechnen von z.B. Druck, ist es wichtig, dass du die Größen aus nur einem Maßsystem nutzt. Wenn du das nämlich nicht tust, bekommst du ein sinnloses Ergebnis verschiedener Einheiten. Also ist es wichtig, dass du die verschiedenen Systeme nicht durcheinander bringst.Hinweis: Bei den Berechnungen ist es wichtig, immer das gleiche Einheitensystem zu verwenden, da sonst die Ergebnisse nicht korrekt sind. -
Abgeleitete Größen und Dimensionen
Abgeleitete Größen werden durch physikalische Operationen zwischen unabhängigen Größen definiert. Geschwindigkeit ist beispielsweise eine physikalische Größe, die durch Division einer zurückgelegten Strecke durch die benötigte Zeit erhalten wird. Die Angabe begegnet uns zum Beispiel im Straßenverkehr, wenn wir 50 "Kilometer pro Stunde", also 50 km/h, fahren. 🚗🏍
Andere abgeleitete Größen sind zum Beispiel Beschleunigung, Kraft, Dichte, Druck und Energie.Dimensionen
Die Kombination von fundamentalen Größen, die verwendet wird, um eine gegebene physikalische Größe zu charakterisieren, wird die Dimension dieser Größe genannt. Die spezifische Dimension ist physikalischer Natur und hängt nicht vom verwendeten Einheitensystem ab.
Um die Dimensionen einer physikalischen Größe anzugeben, werden normalerweise eckige Klammern verwendet. Die Symbole L, M und T repräsentieren die Dimensionen Länge [L], Masse [M] und Zeit [T]. Die abgeleiteten physikalischen Größen können in Form von Potenzen der Fundamentalgrößen
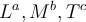 ausgedrückt werden.
ausgedrückt werden.Hier bekommst du einen Überblickt über Dimensionen und Einheiten der abgeleitete Größen des Internationalen Einheitensystems (IS) :
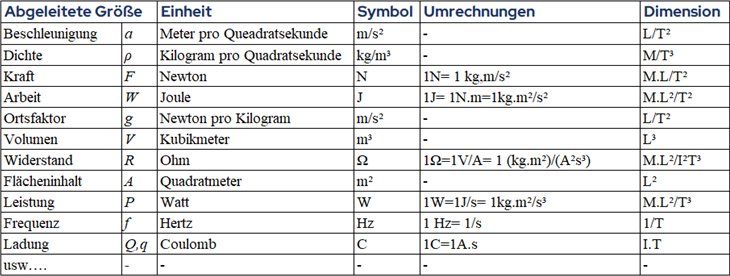
Abgeleitete Größen und Dimensionen des IS. G. Jimenez
-
Dimensionsanalyse
Physikalische Gleichungen müssen Größen konsistent auf ihre Dimensionen beziehen. Eine Bedingung für eine physikalisch sinnvolle Gleichung ist, dass alle Terme - egal ob addiert, subtrahiert oder gleichgesetzt wird - die gleichen Dimensionen haben. Ist diese Bedingung erfüllt, dann ist die Gleichung dimensionshomogen.
Die Dimensionsanalyse macht sich die Tatsache zunutze, dass Dimensionen als algebraische Größen behandelt werden können und ist ein nützliches Werkzeug für:
- Fehler im Ergebnis eines Problems erkennen.
- Zusammenhänge zwischen physikalischen Größen herleiten.
- Enthüllung der Skalierungsgesetze.
Beispiel: Dimensionsanalyse
In manchen Physikübungen sind die Berechnungen so komplex und die Gleichung so lang, dass manchmal überprüft werden muss, ob das gewünschte Ergebnis die gewünschten Dimensionen hat. Lassen wir uns diese physikalische Gleichung analysieren, die die von einem frei fallenden Objekt zurückgelegte Entfernung symbolisiert.
Gleichung: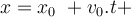
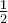
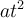 .
.
In dieser Gleichung haben wir Länge, Geschwindigkeit und Beschleunigung an verschiedenen Stellen mit der Zeit multipliziert.
Analysieren wir die Gleichung, so haben wir: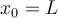

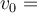
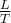
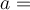
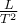
Wenn wir diese Terme in der Gleichung nun durch ihre Dimensionen ersetzen, so bekommen wir folgendes Ergebnis: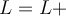 (
(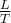 )
)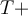 (
(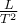 )
)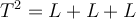 →
→ 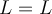 → Länge=Länge
→ Länge=LängeWir können beobachten, dass beim Einsetzen der Dimensionen in jeden der Faktoren der Gleichung das Ergebnis konsistent ist, d. h. wir erhalten kein Ergebnis wie Länge = Geschwindigkeit (würden wir dieses Ergebnis erhalten, hätten wir auf jeden Fall etwas falsch gemacht 😉). Da wir die Länge messen, erwarten wir, dass das Ergebnis Längenmaße hat:
Länge = LängeDimensionen mathematischer Funktionen.
Bei vielen Gelegenheiten ist es üblich, dass eine physikalische Gleichung durch mathematische Funktionen wie trigonometrische Funktionen,
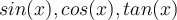 usw. beschrieben wird; durch Logarithmen
usw. beschrieben wird; durch Logarithmen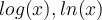 usw. Exponenten
usw. Exponenten 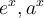 (wobei
(wobei 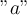 eine Zahl ist). Damit diese mathematischen Funktionen ausgeführt werden können, müssen die Argumente dieser Funktionen dimensionslos sein, d. h.
eine Zahl ist). Damit diese mathematischen Funktionen ausgeführt werden können, müssen die Argumente dieser Funktionen dimensionslos sein, d. h. 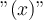 muss keine Dimensionen haben (Dimension= [1] ).
muss keine Dimensionen haben (Dimension= [1] ).Beispiel:
Wir haben die folgende Gleichung, die die Verschiebung einer Welle symbolisiert.
Lösung:
Wir analysieren das Argument der Sinusfunktion (
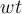 )
)Wir haben gezeigt, dass
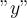 Länge Dimension hat
Länge Dimension hat ![y= [L] y= [L]](https://moodle.thga.de/filter/tex/pix.php/315d8ce827a1ee1ce20de63720221f8d.png) . Dieses Ergebnis ist sinnvoll, da
. Dieses Ergebnis ist sinnvoll, da 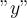 Verschiebung vom Gleichgewichtspunkt bedeutet.
Verschiebung vom Gleichgewichtspunkt bedeutet. -
Skalierungsgesetze 📐
Wenn die linearen Abmessungen eines Objekts im gleichen Verhältnis geändert werden, wird ein dem Original ähnliches Objekt erhalten. Ähnliche Figurenflächen variieren mit dem Quadrat ihrer linearen Dimensionen und ihre Volumina variieren mit dem Kubik ihrer linearen Dimensionen.
Es ist nicht möglich, das Verhalten eines Systems mit einem einfachen Dreisatz von einer Skala auf eine andere Skala zu extrapolieren, sondern es muss das entsprechende Skalengesetz bestimmt werden. Das Verhalten physikalischer Systeme bei der Skalierung hat sehr wichtige praktische Anwendungen. Wird ein großes Objekt auf Basis eines kleinmaßstäblichen Modells entworfen, müssen Änderungen seiner physikalischen Eigenschaften berücksichtigt werden.
Beispiel:
Wir haben die Maße der Breite (b) und Länge (a) einer Hand. Die Handfläche und das Volumen der Hand werden nicht linear zunehmen, wenn man die Größe erhöht. Stell dir vor, du möchtest die Hand auf das Doppelte vergrößern (wie man eine Hand vergrößert wenn es nicht gerade eine aufblasbare "Winkehand" aus dem Stadion ist ist eine ganz andere Frage, der wir hier nicht auf den Grund gehen ✋ 🤚 😉) und du verdoppelst nur ihre Abmessungen und berechnest dann die Fläche. Wenn wir annehmen, dass die Hand ein Rechteck ist, so wird die Fläche als Multiplikation ihrer Seiten a*b berechnet.
Für die kleine Hand gilt die Fläche
 .
.
Nun wollen wir, dass die Fläche zweimal vergrößert wird, daher könnten wir folgendes annehmen: t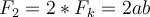
Allerdings wurden die Werte (Breite b und Länge a) zweimal vergrößert: und
und 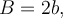
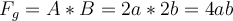 - Das Ergebnis ist also nicht das Gleiche!
- Das Ergebnis ist also nicht das Gleiche! Vergleich der vorherigen Ergebnisse
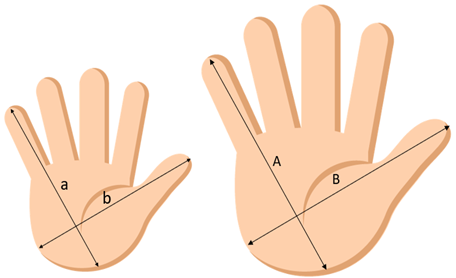
Skalierung. G.Jimenez Es ist ersichtlich, dass das Verdoppeln jeder Dimensionen einzeln nicht bedeutet, dass das Ergebnis dem Doppelten entspricht. In diesem Fall war das Ergebnis bei einer Fläche viermal größer. Dies bedeutet, dass die Fläche der Objekte in der Potenz 2 (und das Volumen in der Potenz 3) zunimmt.Beispiel 2:
Ein 3x2 Meter großes Brett kostet im Baumarkt 50 Euro. Wie viel kostet ein 6x4 Meter großes Brett? Nutze die Skalierungsgesetze um den neuen Preis zu errechnen.
Wir sehen, dass das Ergebnis viermal größer ist, obwohl sich jede Dimension nur verdoppelt hat.
Ein weiteres Beispiel zur Skalierung kannst du dir nun noch als Video ansehen. 🎬
Hinweis: In Skalierungsfällen wird der Dreisatz mit Flächen oder Volumen durchgeführt.Bevor du den Dreisatz anwendest, bestimme zunächst, wie viele Dimensionen das zu skalierende Objekt hat. Ob das Objekt eindimensional (1D), zweidiemensional (2D) oder dreidimensional (3D) ist.
- Verwende für 2D-Objekte die Flächengleichungen.
- Verwende für 3D-Objekte die Volumengleichungen.
-
Wissenschaftliche Schreibweise 💯
Im Folgenden erfährst du was es mit der wissenschaftlichen Schreibweise auf sicht hat. Du kannst dir Schritt für Schritt die Informationen durchlesen oder auch direkt weiter herunterscrollen und dir den gleichen Inhalt als Video ansehen. 🎥Physikalische Größen können nur mit einer gewissen Genauigkeit gemessen werden, weswegen ihre Zahlenwerte mit der richtigen Anzahl an signifikanten Ziffern angegeben werden müssen. Also nur mit den Ziffern, die mit hinreichender Sicherheit bekannt sind, da sie die Einzigen sind, die physikalische Bedeutung haben.
Bei der Verwendung eines Taschenrechners ist es ein häufiger Fehler, alle vom Taschenrechner ausgespuckten Zahlen in die endgültige Antwort der Berechnung zu schreiben.
Angenommen, wir wollen das Volumen einer Kugel berechnen, deren Radius auf drei signifikanten Stellen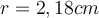 bekannt ist.
bekannt ist. Mit dem Taschenrechner ergibt sich das Ergebnis
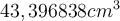 . Wir wollen nun aber nicht die Zahl genauso vom Taschenrechner übernehmen, sondern das Ergebnis mit der richtigen Anzahl an signifikanten Ziffern angeben. Das heißt es muss eine
Anzahl von Ziffern beibehalten werden, die nicht größer ist, als die kleinste
Anzahl signifikanter Ziffern der an der Operation beteiligten Zahlen. In diesem
Beispiel sind die Werte der numerischen Konstanten
. Wir wollen nun aber nicht die Zahl genauso vom Taschenrechner übernehmen, sondern das Ergebnis mit der richtigen Anzahl an signifikanten Ziffern angeben. Das heißt es muss eine
Anzahl von Ziffern beibehalten werden, die nicht größer ist, als die kleinste
Anzahl signifikanter Ziffern der an der Operation beteiligten Zahlen. In diesem
Beispiel sind die Werte der numerischen Konstanten 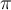 und
und 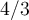 genau bekannt. Die kleinste Anzahl signifikanter Ziffern von den bekannten Zahlen hat der Wert
genau bekannt. Die kleinste Anzahl signifikanter Ziffern von den bekannten Zahlen hat der Wert 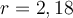 mit drei signifikanten Stellen. Dies bedeutet, dass wir als Ergebnis ebenfalls einen Wert mit drei signifikanten Stellen angeben. Unser Ergebnis lautet also
mit drei signifikanten Stellen. Dies bedeutet, dass wir als Ergebnis ebenfalls einen Wert mit drei signifikanten Stellen angeben. Unser Ergebnis lautet also 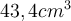 .
.In der Physik gibt es aber noch mehr Stolpersteine. Meist werden Sachen berechnet, bei denen ein sehr kleines Ergebnis (
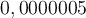 Meter) oder ein sehr großes Ergebnis (
Meter) oder ein sehr großes Ergebnis (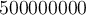 Meter) herauskommt. Da diese Angabe für uns jedoch recht unübersichtlich ist, gibt es eine bessere Methode diese Ergebnisse aufzuschreiben. Diese Methode wird auch wissenschaftliche Schreibweise genannt. Dabei werden einfach die Nullen als Zehnerpotenz aufgeschrieben. Um die Zehnerpotenz zu ermitteln, wird die Anzahl der Stellen vor dem Dezimalkomma von rechts nach links bis direkt vor der ersten Ziffer ermittelt. Diese Anzahl schreibst du dann als hochgestellte Zahl rechts neben die Zehn.
Meter) herauskommt. Da diese Angabe für uns jedoch recht unübersichtlich ist, gibt es eine bessere Methode diese Ergebnisse aufzuschreiben. Diese Methode wird auch wissenschaftliche Schreibweise genannt. Dabei werden einfach die Nullen als Zehnerpotenz aufgeschrieben. Um die Zehnerpotenz zu ermitteln, wird die Anzahl der Stellen vor dem Dezimalkomma von rechts nach links bis direkt vor der ersten Ziffer ermittelt. Diese Anzahl schreibst du dann als hochgestellte Zahl rechts neben die Zehn.
Beispiel:
Bei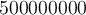 Metern zählen wir Acht Nullen und schreiben diese Anzahl als hochgestellte Zahl rechts neben die Zehn, d.h. die wissenschaftliche Schreibweise ist somit
Metern zählen wir Acht Nullen und schreiben diese Anzahl als hochgestellte Zahl rechts neben die Zehn, d.h. die wissenschaftliche Schreibweise ist somit 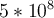 .
.Fast genauso funktioniert das Ganze auch für sehr kleine Zahlen. Dabei ist aber wichtig zu beachten, dass die Zehnerpotenz hier negativ ist! In diesem Fall werden die Stellen ab dem Dezimalkomma nach rechts bis hinter die erste Ziffer, die nicht Null ist, gezählt.
Beispiel:
Für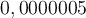 Meter zählen wir sieben Stellen nach dem Komma bis hinter die erste Ziffer, die nicht Null ist und schreiben die Anzahl als negative hochgestellte Zahl rechts neben die Zehn, d.h. die wissenschaftliche Schreibweise ist
Meter zählen wir sieben Stellen nach dem Komma bis hinter die erste Ziffer, die nicht Null ist und schreiben die Anzahl als negative hochgestellte Zahl rechts neben die Zehn, d.h. die wissenschaftliche Schreibweise ist 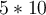 -7 mit einer einzigen signifikanten Zahl und
-7 mit einer einzigen signifikanten Zahl und 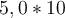 -7 mit zwei signifikanten Stellen usw.
-7 mit zwei signifikanten Stellen usw.Einige Regeln für das korrekte Schreiben von signifikanten Stellen:
1. Bei jeder mathematischen Operation (Addition, Subtraktion, Multiplikation, Division) muss das Ergebnis die gleiche Anzahl signifikanter Stellen haben, wie der kleinste der Operatoren. Ebenso müssen die gleiche Anzahl von Dezimalstellen beibehalten und die Rundungsregeln verwendet werden.
Beispiele:
2. Wenn mathematische Berechnungen physikalisch sinnvoll sind, ist es immer gut zu bedenken, dass als Ergebnis nur die Dezimalstellen verwendet werden.
Beispiel:
Wenn wir sagen, dass ein Auto 89 m in 3 s zurücklegt, meinen wir eigentlich 89,0 m in 3,00 s, was einer Geschwindigkeit von 29,7 m/s entspricht.3. Für sehr kleine oder sehr große Zahlen gibt es die wissenschaftliche Notation. Diese stellt eine Möglichkeit dar, Werte in Form einer Zehnerpotenz anzugeben. Es ist zu beachten, dass für die korrekte Verwendung dieses Schreibweise, die signifikanten Zahlen berücksichtigt werden müssen. Zur Bestimmung der Zehnerpotenz von sehr großen Zahlen wird die Anzahl der Stellen vor dem Komma von rechts nach links bis vor die erste Ziffer bestimmt. Dann wird diese Zahl als hochgestellte Zahl rechts von Zehn notiert. Zur Bestimmung der Zehnerpotenz von sehr kleinen Zahlen werden die Stellen ab dem Dezimalkomma nach rechts bis hinter die erste Ziffer, die nicht Null ist, gezählt. und diese Zahl als hochgestellte negative Zahl rechts von Zehn notiert.4. In wissenschaftlicher Schreibweise werden nur die signifikanten Zahlen der führenden Zahl gezählt, nicht die Potenz.Beispiele:
Wissenschaftliche Schreibweise. G. Jimenez Merke: Ist die Zahl größer als Eins, so ist der Exponent in der wissenschaftlichen Schreibweise positiv. Ist die Zahl kleiner als Eins, so ist der Exponent negativ! Ein Klacks oder? 😉Nun gibt es noch mal eine Zusammenfassung als Video 🎬 Fall das Video nicht sofort lädt, hab bitte einen kurzen Moment Geduld. 🙄

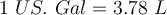
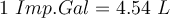
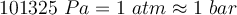
![[X] = Dimension von X [X] = Dimension von X](https://moodle.thga.de/filter/tex/pix.php/918e5c52f2a3765c4b609341a3ac2959.png)