Kinematik II
Abschnittsübersicht
-
Willkommen zum zweiten Kinematik-Modul 👋
Da wir davon ausgehen, dass du das erste Modul (Kinematik I) bereits hinter dir hast, halten wir uns gar nicht erst mit einer langen Einleitung auf ...
Sollte dies nicht der Fall sein so empfehlen wir dir erst einen Blick in Kinematik I zu werfen und dann noch mal hierher zurückzukommen. 😉
In Kinematik I gibt es eine allgemeine Einführung während wir hier direkt zur Sache kommen und sich alles um Kreisbewegungen dreht. 🌌
Am Ende dieses Modul solltest du:
- Das Konzept von Kreisbewegungen, sowie die Unterschiede zwischen gleichmäßigen und ungleichmäßigen Kreisbewegungen kennen und verstehen.
- Kreisbewegungen durch Gleichungen beschreiben.
- Das Polarkoordinatensystem kennen und anwenden.
Bevor du startest haben wir noch einige Infos für dich zusammengestellt:
Das Modul ist so aufgebaut, dass du zunächst den Eingangstest ausprobieren solltest. Auf Basis dessen bekommst du von uns eine Empfehlung, mit welchem Level der Übungen du in den jeweiligen Themen fortfahren solltest. Die Entscheidung darüber bleibt aber dir überlassen, du kannst auch jederzeite andere Übungen mitmachen! Zum Schluss solltest du allerdings den Abschlusstest nicht vergessen! Dieser ermöglicht es dir dein Wissen anzuwenden und gibt dir eine Rückmeldung zu deinem Fortschritt. 🧐
Die Bearbeitunsgdauer für das gesamte Modul kann bis zu 60 Minuten dauern. ⌛️ Vielleicht bist du aber auch schneller fertig. 🤭 Unsere Zeitangabe ist nur eine ungefähre Einschätzung die darauf basiert, dass du dir alle Inhalte ansiehst und jede einzelne Rechnung in allen Leveln durchführst. Du kannst aber natürlich frei entscheiden wann du dir welche Inhalte anguckst und das Modul jederzeit verlassen, wieder zurückkommen und dort weitermachen wo du aufgehört hast. ⏯Um alle Funktionen des Moduls nutzen zu können, musst du dich oben rechts über das kleine Zahnrad einschreiben. ⚙️✏️-
Kreisbewegungen 🎡
Kreisbewegungen spielen in unserem Alltag in verschiedenen Bereichen eine wichtige Rolle. Wir kennen sie beispielweise als Karussell, Waschmaschine, Kreisverkehr oder aber als Windrad. Die Kreisbewegung ist ein Sonderfall der Bewegung in einer Ebene und tritt auf, wenn der Pfad, dem das Teilchen folgt, ein Kreis ist. Die Kreisbewegung hat eine große praktische Bedeutung, da sie in der Natur und in unserer täglichen Erfahrung sehr verbreitet ist. Neben den oben genannten Beispielen sind es auch die Bewegungen der Räder von Autos und Fahrrädern um ihre Achsen und die Annäherung an die Bewegung eines künstlichen Satelliten um unsere Erde. 🌏
Um das Thema besser zu verstehen, ist es notwendig, einige grundlegende Konzepte zu dieser Bewegung zu beschreiben. Zum Schluss wird dein Verständnis mit einer Übung überprüft, in der du diese Grundkonzepte noch mehr festigst. Also worauf wartest du ⁉️ Ran an den Speck! 🥓
Kreisförmige Position
Ein Objekt in Kreisbewegung um einen Ursprungspunkt
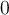 kann in einem Bezugssystem durch den radialen Abstand
kann in einem Bezugssystem durch den radialen Abstand 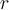 und den Winkel
und den Winkel 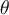 gemessen von der x-Achse lokalisiert werden. Der Abstand
gemessen von der x-Achse lokalisiert werden. Der Abstand 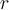 ist konstant und der Winkel
ist konstant und der Winkel  wird als Winkelposition bezeichnet. Bei der Beschreibung einer Kreisbewegung ist es zweckmäßig, die Winkel in Radianten auszudrücken, die durch das Verhältnis zweier Längen definiert sind: dem Bogen
wird als Winkelposition bezeichnet. Bei der Beschreibung einer Kreisbewegung ist es zweckmäßig, die Winkel in Radianten auszudrücken, die durch das Verhältnis zweier Längen definiert sind: dem Bogen  und dem Radius
und dem Radius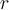 . Ein Radiant ist der Winkel, der von einem Bogen der Länge
. Ein Radiant ist der Winkel, der von einem Bogen der Länge eingeschlossen wird, der im Wert gleich dem Radius
eingeschlossen wird, der im Wert gleich dem Radius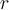 des Umfangs ist.
des Umfangs ist.

Kreisförmige Position. G. Jimenez Für weitere Details zur mathematischen Beschreibung von kreisförmigen Positionen und insbesondere dem Einheitskreis, empfehlen wir dir einen Abstecher in das Trigonometrie-Modul zu machen. 💡Winkelgeschwindigkeit
Die mittlere Winkelgeschwindigkeit ist definiert als der pro Zeiteinheit überstrichene Winkel:
Die momentane Winkelgeschwindigkeit erhält man, indem man ein extrem kleines Zeitintervall nimmt:
Eigentlich ist
 die Winkelgeschwindigkeit oder der Größe von
die Winkelgeschwindigkeit oder der Größe von 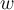 , da die Winkelgeschwindigkeit ein Vektor ist, dessen Richtung senkrecht zur Bewegungsebene gewählt wird.
, da die Winkelgeschwindigkeit ein Vektor ist, dessen Richtung senkrecht zur Bewegungsebene gewählt wird.Winkelbeschleunigung
Die Winkelbeschleunigung drückt die zeitliche Änderung der Winkelgeschwindigkeit
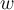 aus.
aus.Konstante Winkelbeschleunigung
Es wird beobachtet, dass die Definitionen der Winkelvariablen denen der linearen Bewegung analog sind. Daher ähneln die zugehörigen kinematischen Gleichungen
 und
und  für konstante Winkelbeschleunigung ihren Gegenstücken für die linearen Variablen
für konstante Winkelbeschleunigung ihren Gegenstücken für die linearen Variablen  und
und  .
.Lineare Geschwindigkeit und Winkelgeschwindigkeit
Ein Teilchen, das sich auf einem Umfang bewegt, hat eine momentane lineare Geschwindigkeit
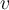 , die tangential zu seiner Bahn ist. Wir können eine durchschnittliche lineare Geschwindigkeit als das Verhältnis der Länge des zurückgelegten Bogens delta s zu der Zeit, die benötigt wird, um ihn zurückzulegen,
, die tangential zu seiner Bahn ist. Wir können eine durchschnittliche lineare Geschwindigkeit als das Verhältnis der Länge des zurückgelegten Bogens delta s zu der Zeit, die benötigt wird, um ihn zurückzulegen, 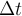 definieren.
definieren.In der
 , erhält man die momentane Geschwindigkeit oder den Betrag des Geschwindigkeitsvektors:
, erhält man die momentane Geschwindigkeit oder den Betrag des Geschwindigkeitsvektors:





Da die differentielle Länge des Bogens
 ist, können wir
ist, können wir  durch
durch  ausdrücken
ausdrücken
Lineargeschwindigkeit und Winkelgeschwindigkeit. G. Jimenez Gleichförmige Kreisbewegung
Bei einer gleichförmigen Kreisbewegung ist der Betrag des Vektors (der Geschwindigkeit) konstant, aber die tangentiale Richtung von
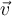 ändert sich kontinuierlich. Aufgrund dieser Richtungsänderung ist eine gleichförmige Kreisbewegung
immer eine beschleunigte Bewegung. Der Beschleunigungsvektor
ändert sich kontinuierlich. Aufgrund dieser Richtungsänderung ist eine gleichförmige Kreisbewegung
immer eine beschleunigte Bewegung. Der Beschleunigungsvektor 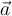 steht senkrecht auf diesem Umfang und zeigt immer zur Mitte hin. Deshalb wird in diesem Zusammenhang auch von Radial- oder Zentripetalbeschleunigung gesprochen.
steht senkrecht auf diesem Umfang und zeigt immer zur Mitte hin. Deshalb wird in diesem Zusammenhang auch von Radial- oder Zentripetalbeschleunigung gesprochen.
Gleichförmige Kreisbewebung. G. Jimenez Ungleichmäßige Kreisbewegung
Bei einer ungleichförmigen Kreisbewegung variiert das Geschwindigkeitsgröße an jedem Punkt und es gibt eine tangentiale Beschleunigungskomponente, sodass der Beschleunigungsvektor zwei Komponenten hat:
Die Radialbeschleunigung ist der Richtungsänderung von
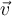 zugeordnet
zugeordnetDie Tangentialbeschleunigung ist mit der Variation des Größe von
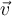 verbunden:
verbunden:Dabei ist
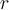 der Radius des Umfangs
der Radius des Umfangs 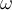 und die Winkelgeschwindigkeit
und die Winkelgeschwindigkeit  und
und  die Winkelbeschleunigung
die Winkelbeschleunigung  .
.
Ungleichmäßige Kreisbewegung (Beschleunigungsvektoren) . G. Jimenez -
Polar-Koordinaten
Bei der Vektoranalyse von Kreisbewegungen ist es einfacher, ein Polarkoordinatensystem zu verwenden, da dieses ein zweidimensionales Koordinatensystem ist.
In diesem System ist die Position eines Punktes P, der die kartesischen Echokoordinaten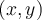 hat, durch seinen Abstand zum Ursprung,
hat, durch seinen Abstand zum Ursprung,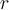 , und durch den Winkel
, und durch den Winkel 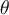 (gemessen in Bezug auf die x-Achse in der Richtung gegen den Uhrzeigersinn) festgelegt.
(gemessen in Bezug auf die x-Achse in der Richtung gegen den Uhrzeigersinn) festgelegt.Wir können die Positionsvektoren
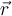 , die Geschwindigkeit
, die Geschwindigkeit 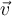 und die Beschleunigung
und die Beschleunigung 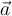 in Bezug auf die Einheitspolarvektoren schreiben.
in Bezug auf die Einheitspolarvektoren schreiben.
Polar Koordinaten. G.Jimenez Der radiale Einheitsvektor
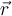 hat die Richtung des Positionsvektors und der polare Einheitsvektor
hat die Richtung des Positionsvektors und der polare Einheitsvektor  steht senkrecht auf dem vorherigen. Diese Vektoren können als kartesische Einheitsvektoren
steht senkrecht auf dem vorherigen. Diese Vektoren können als kartesische Einheitsvektoren  geschrieben werden. Der radiale Einheitsvektor ist:
geschrieben werden. Der radiale Einheitsvektor ist:Der tangentiale Einheitsvektor
 wird unter Berücksichtigung von
wird unter Berücksichtigung von  und dessen Größe Eins erhalten:
und dessen Größe Eins erhalten:die zeitlichen Ableitungen der polaren Einheitsvektoren
 (r, Theta) sind nicht Null:
(r, Theta) sind nicht Null:
Polarische Einheitsvektoren von G.Jimenez. Geschwindigkeits- und Beschleunigungsvektoren
Bei einer Kreisbewegung ist der Geschwindigkeitsvektor v immer tangential zum Umfang und hat die Richtung der Tangentialeinheit des Vektors theta:
Der Beschleunigungsvektor ist die zeitliche Ableitung von
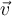 , also:
, also:Unter Berücksichtigung von
 sehen wir, dass die Beschleunigung zwei Komponenten hat:
sehen wir, dass die Beschleunigung zwei Komponenten hat:Der erste Term ist die radiale Komponente
 und das negative Vorzeichen bedeutet, dass sie zum Mittelpunkt des Kreises und entgegengesetzt zum Einheitsvektor
und das negative Vorzeichen bedeutet, dass sie zum Mittelpunkt des Kreises und entgegengesetzt zum Einheitsvektor 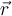 gerichtet ist. Der zweite Term ist die Tangentialkomponente "
gerichtet ist. Der zweite Term ist die Tangentialkomponente " ".
".
Beschleunigungsvektoren in Polarkoordinaten von G.Jimenez.















![[rad/s] [rad/s]](https://moodle.thga.de/filter/tex/pix.php/781f336a921a9c02fe832c465f8ba45d.png)


![[Hz] [Hz]](https://moodle.thga.de/filter/tex/pix.php/7f4f1b9f245eab6e1e0d66019258ee47.png)

![[s] [s]](https://moodle.thga.de/filter/tex/pix.php/109b29d0bf63ab9c7746a4c60e5f7181.png)















![r= \sqrt[2]{x^2+y^2} r= \sqrt[2]{x^2+y^2}](https://moodle.thga.de/filter/tex/pix.php/e4713a0050edd119b53bdd54042046b8.png)

![d= \sqrt[]{r_1^2 +r_2^2 -2r_1.r_2cos( \theta _1+\theta_2 )} d= \sqrt[]{r_1^2 +r_2^2 -2r_1.r_2cos( \theta _1+\theta_2 )}](https://moodle.thga.de/filter/tex/pix.php/ab47dddb97fbcd1a4da356e5918eaee3.png)



















