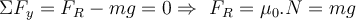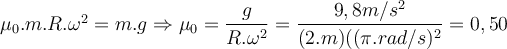Dynamik I
Abschnittsübersicht
-
In diesem Modul lernen wir das Thema Dynamik kennen. Dynamik ist der Zweig der Mechanik, in dem Fragen beantwortet werden können, wie z. B. was dazu führt, dass sich ein stationäres Objekt in Bewegung setzt oder was ein Objekt beschleunigt oder verlangsamt?
In der Dynamik werden zwei grundlegende Elemente und Konzepte verwendet: Masse und Kraft!. Diese sind verantwortlich für die Bestimmung der Wechselwirkungen, die zwischen dem Körper und einem anderen Körper in seiner Umgebung bestehen. Die Dynamik basiert auf den drei Gesetzen, die von Isaac Newton 1687 formuliert wurden. Diese Gesetze sind als Ergebnis der Verallgemeinerung der Erkenntnisse von Newton und anderen Wissenschaftlern, die ihm vorausgingen, insbesondere Galileo, entstanden. Die drei Newtonschen Gesetze sind ein logisches, strenges und geschlossenes System von Prinzipien, die die Säulen der klassischen oder Newtonschen Mechanik bilden.
Am Ende dieses Modul solltest du:
- das Konzept der Kraft und der Bewegung von Körpern verstehen
- Newtonsche Gesetze kennen
- Bezugssystemen der Trägheitskräfte analysieren
- Strategien zur Problemlösung entwickeln.
- die Anwendungen der Newtonschen Gesetze in Federn, Kreisbewegungen und beschleunigten Systemen üben und analysieren.
Bevor du beginnst, noch kurz einige Infos zum Ablauf: Das Modul ist so aufgebaut, dass du mit dem Eingangstest starten solltest. Als Ergebnis bekommst eine Empfehlung, mit welchem Level der Übungen du in den jeweiligen Themen fortfahren solltest. Du kannst dieser Empfehlung folgen oder aber selber entscheiden welche Inhalte du dir ansehen und welche Übungen du machen möchtest. Zum Schluss solltest du dann den Abschlusstest absolvieren, an dessen Ende dich wiederum ein Feedback erwartet. 🙌
Die Bearbeitunsgdauer für das gesamte Modul kann bis zu 2,5 Stunden betragen ⌛️ Wirkt das abschreckend? Dann lies besser noch etwas weiter. 😉 Es ist nur eine ungefähre Einschätzung die darauf basiert, dass du dir alle Inhalte ausführlich ansiehst und jede einzelne Rechnung in allen Leveln durchführst. Du entscheidest allerdings frei in welchem Tempo du dir das Modul ansehen und welche Übungen du machen möchtest. Außerdem kannst du das Modul jederzeit verlassen und zurückkommen und dort weitermachen wo du aufgehört hast. ⏯-
Einführung: Dynamik ≠ Kinematik 📝
Weißt du schon was Dynamik ist und was diese mit Mechanik zu tun hat ❓Die Mechanik lässt sich in zwei große Teilbereiche gliedern: Kinematik und Dynamik. Die Kinematik untersucht die zeitlichen Ausprägungen einer Bewegung, eine Analyse der Bewegungsursache findet hier nicht statt (für weitere Infos geht's hier zum 👉 PepperMINT Kinematik Modul).
Die Dynamik beschäftigt sich mit den zeitlichen Änderungen der Größen in einer Bewegung, das heißt, hier erfolgt eine Analyse der Bewegungsursache. Außerdem ist die Kraft die wesentliche Größe im Bereich der Dynamik, welche sich weiter in die Bereiche Kinetik und Statik unterteilen lässt. Während sich die Kinetik mit bewegten Systemen auseinandersetzt, beschäftigt sich die Statik mit ruhenden Systemen.
Nachfolgend haben wir dir noch einige hilfreiche Links zusammengestellt. 💡 Probiere diese gerne aus oder starte direkt mit dem Lückentext.
Der nachfolgende Link führt zu einer externen Internetseite, die ggf. andere Datenschutzvorgaben erfüllt als wir es auf dieser Plattform tun. Dabei können Daten von dir übertragen und weiterverarbeitet werden. Wenn du dich allgemein zum Thema Datenschutz erkundigen möchtest, empfehlen wir dir die Erklärvideos der Initiative Datenschutz geht zur Schule.Diese 👉 Simulation 👈 dient dazu dir einen Überblick über das Thema Dynamik zu verschaffen.Die Dynamik lässt sich in zwei Gebiete unterteilen:
1️⃣Statik: behandelt den Fall des Kräftegleichgewichts (unbeschleunigte Körper)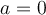
2️⃣Kinetik: befasst sich mit beschleunigten Körpern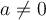
-
Kraft und Bewegung
Der Kraftbegriff
Die intuitive Vorstellung von Kraft kennen wir aus alltäglichen Erfahrungen. 💡 Wir identifizieren normalerweise eine Kraft mit jeder Art von „Ziehen“ oder „Schieben“. Kraft ist eine physikalische Größe, die einen Körper und seine Umgebung charakterisiert und quantifiziert. Die Wirkung einer Kraft auf einen Körper besteht darin ihn zu verformen (d. h. seine Größe und Form zu ändern) oder seinen Bewegungszustand zu verändern.
Eine Kraft ist in der Lage, einen Körper zu beschleunigen. Ihr kann eine Größe, eine Richtung und ein Sinn zugeordnet werden. Darüber hinaus können wir Kräfte nach den Regeln der Vektoraddition kombinieren, daher ist die Kraft selbst eine Vektorgröße und wir können sie durch einen Pfeil darstellen, wie in der nachfolgenden Abbildung zu sehen.
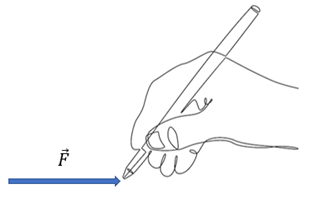
Kraft, eine Vektorgröße von G. Jimenez Gesamtkraft
Wenn mehrere Kräfte auf einen Körper wirken, wird der Vektor oder die resultierende Summe aller Kräfte als Nettokraft bezeichnet.
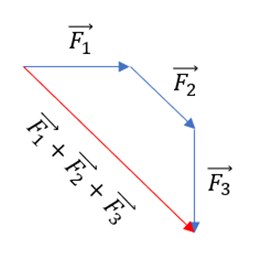
Gasamtkraft von G. Jimenez Die allein wirkende Gesamtkraft erzeugt dieselbe Wirkung wie das System verschiedener Kräfte, die sie ersetzt und bildet. Im Fall von
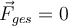 werden diese Kräfte als ausgeglichen bezeichnet.
werden diese Kräfte als ausgeglichen bezeichnet.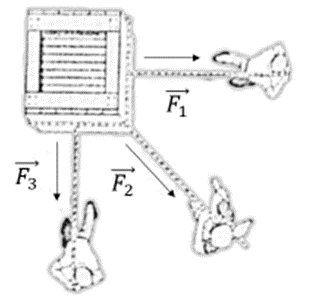
Gesamtkraft von N. Donner -
Die newtonsche Gesetze
Das Grundproblem der Dynamik besteht darin, die Gesetzmäßigkeiten aufzustellen, die die Kräfte mit dem Bewegungszustand eines Körpers verknüpfen. Isaac Newton hat dazu drei Grundsätze der Bewegungslehre formuliert. Diese sind unter den Formulierungen Newtonsche Gesetze, Newtonsche Prinzipien oder auch Newtonsche Axiome bekannt.
Wir haben uns dafür entschieden den Begriff Newtonsche Gesetze zu gebrauchen. Los geht's, schauen wir uns die drei Gesetze einmal an:
Newtons erstes Gesetz
Die Grundlagen für Newtons erstes Gesetz stammen von Galileo, der in seiner Forschung eine natürliche Tendenz von Objekten erkannte, ihren anfänglichen Bewegungszustand beizubehalten. Diese Tendenz nannte er Trägheit. Newtons erstes Gesetz ist den Schlussfolgerungen von Galileo sehr ähnlich und besagt, dass:
„Jeder Körper in einem Zustand der Ruhe oder in gleichförmiger geradliniger Bewegung bleibt in diesem Zustand, wenn nicht eine Nettokraft auf ihn einwirkt."
Das heißt, wenn die Geschwindigkeit eines Körpers nicht konstant ist, folgern wir, dass eine Nettokraft auf den Körper wirken muss.

Abb. basierend auf: GodfreyKneller-IsaacNewton-1689.jpg
von Godfrey Kneller ist als
Creative Commons Public Domain (CC0)
gekennzeichnet.- Masse:
Die intuitive Vorstellung, die wir alle von Masse haben, ist die, dass es etwas mit dem Ausmaß oder dem Gewicht einer Person oder eines Gegenstandes zu tun hat. Physikalisch formuliert, entspricht die Masse
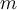 der Menge an Materie, die ein Körper besitzt. Genauer gesagt können wir sagen, dass Masse die Eigenschaft ist, die einem Körper seine Trägheit oder natürliche Tendenz verleiht, seinen Ruhezustand beizubehalten oder in Bewegung zu bleiben. Je mehr Masse ein Körper hat, desto schwieriger ist es, ihn unter Einwirkung einer Kraft zu bewegen oder seine Geschwindigkeit zu ändern. Das kennen wir auch aus dem Alltag: Um einen Kasten Wasser hochzuheben, Bedarf es einer größeren Anstrengung als wenn ich nur eine einzelne Flasche aus dem Kasten entnehme, wenn zwei Autos unterschiedlich groß und schwer sind, aber die gleiche Anzahl an PS haben, dann werden wir das kleinere und leichtere Auto deutlich schneller beschleunigen können als das größere usw. 😉
der Menge an Materie, die ein Körper besitzt. Genauer gesagt können wir sagen, dass Masse die Eigenschaft ist, die einem Körper seine Trägheit oder natürliche Tendenz verleiht, seinen Ruhezustand beizubehalten oder in Bewegung zu bleiben. Je mehr Masse ein Körper hat, desto schwieriger ist es, ihn unter Einwirkung einer Kraft zu bewegen oder seine Geschwindigkeit zu ändern. Das kennen wir auch aus dem Alltag: Um einen Kasten Wasser hochzuheben, Bedarf es einer größeren Anstrengung als wenn ich nur eine einzelne Flasche aus dem Kasten entnehme, wenn zwei Autos unterschiedlich groß und schwer sind, aber die gleiche Anzahl an PS haben, dann werden wir das kleinere und leichtere Auto deutlich schneller beschleunigen können als das größere usw. 😉
Nach einem von Mach vorgeschlagenen Verfahren können wir die Trägheitsmassen zweier Körper aus den Beschleunigungen vergleichen, die sie unter der Wirkung derselben Kraft erhalten. Angenommen, auf einer reibungsfreien Oberfläche werden zwei Blöcke mit einer zwischen ihnen zusammengedrückten Feder in Ruhe platziert. Wenn das System freigegeben wird, bewegen sich die Blöcke in entgegengesetzte Richtungen, sodass der leichtere Block eine größere Beschleunigung erhält. Da die Masse ein Maß für den Widerstand gegen Geschwindigkeitsänderungen ist, können wir die Beziehung zwischen den Massen zweier Körper als das Gegenteil der Beziehung zwischen den Beschleunigungen definieren, die sie erhalten.Wenn wir in einem solchen Experiment für einen der Körper eine Masse von 1 kg als Bezugsnormal wählen, können wir durch Vergleichen die Masse jedes anderen Körpers bestimmen.
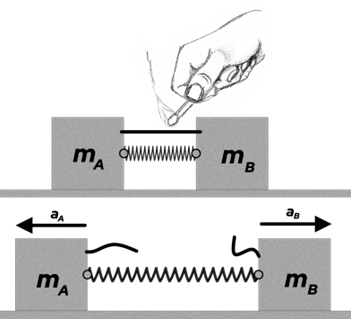
Machs Methode zum Vergleich von Trägheitsmassen. N. Donner
Newtons zweites GesetzDas zweite Newtonsche Gesetz drückt aus und quantifiziert, was mit einem Körper passiert, wenn eine Nettokraft auf ihn einwirkt:
"Die Beschleunigung eines Körpers ist direkt proportional zu der auf ihn wirkenden Nettokraft und umgekehrt proportional zu seiner Masse."
Die Proportionalitätskonstante wird zweckmäßigerweise gewählt, um die Krafteinheit so zu definieren, dass das Produkt aus der Masse des Körpers und seiner Beschleunigung gleich der Nettokraft ist.
Die Richtung des Beschleunigungsvektors stimmt mit der der Nettokraft überein, unabhängig von der Richtung des Geschwindigkeitsvektors. In dem besonderen Fall, dass die Nettokraft Null ist, ist die Beschleunigung Null und der Körper bleibt in Ruhe oder in gleichförmiger Bewegung, was mit dem ersten Hauptsatz übereinstimmt.
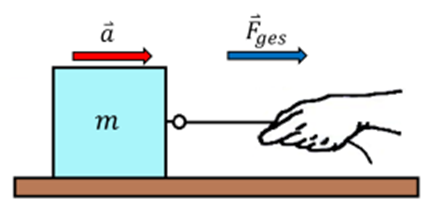
Newtons zweites Gesetz von G. Jimenez Newtons drittes Gesetz
Das erste und das zweite Gesetz befassen sich mit dem Verhalten eines einzelnen Körpers, das dritte Gesetz bezieht sich auf die gegenseitige Interaktion zwischen zwei verschiedenen und getrennten Körpern.
„Immer wenn ein Körper A eine Kraft auf einen Körper B ausübt, übt der Körper B eine Kraft auf den Körper A aus, unabhängig von der Größe, aber in die entgegengesetzte Richtung.“
Das dritte Gesetz wird manchmal das Gesetz von Aktion und Reaktion genannt: Zu jeder Aktion gibt es eine entsprechende Reaktion. Um Verwirrung zu vermeiden, ist es wichtig zu bedenken, dass Aktions- und Reaktionskräfte auf unterschiedliche Objekte wirken.
Für jede Kraft (Aktion) gibt es eine gleiche und entgegengesetzte Kraft (Reaktion)
Newtons drittes Gesetz: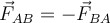
Schauen wir uns einige Beispiele für Aktions- und Reaktionspaare an:
- Wir können vorwärts gehen, weil der Boden unsere Füße in diese Richtung drückt, wenn wir uns gegen den Boden drücken.
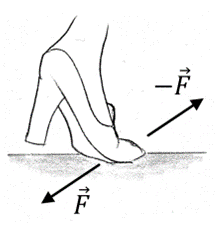
- Wenn ein Nagel eingetrieben wird, ist die vom Hammer auf den Nagel ausgeübte Kraft (die Aktion) gleich und entgegengesetzt zu der Kraft, die der Nagel auf den Hammer ausübt (die Reaktion).
- In Abbildung
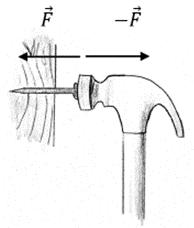
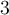 übt die an die Wand gelehnte Person eine Kraft auf die Wand aus, die Reaktion der Wand ist eine gleiche und entgegengesetzte Kraft, die die Person drückt.
übt die an die Wand gelehnte Person eine Kraft auf die Wand aus, die Reaktion der Wand ist eine gleiche und entgegengesetzte Kraft, die die Person drückt.
1.
 2.
2. 3.
3. 
Newtons drittes Gesetz von N. Donner
Gewicht und Masse eines KörpersMasse und Gewicht beziehen sich auf zwei verschiedene Eigenschaften eines Körpers.
- Die Masse ist eine grundlegende und inbegriffen Eigenschaft eines bestimmten Körpers, die seine Trägheit bestimmt, d.h. seinen Widerstand gegen die Änderung seines Bewegungszustands.
- Gewicht ist die gravitative Anziehungskraft, die ein Himmelskörper (bei uns die Erde) auf einen Körper bestimmter Masse ausübt.
Wenn wir im zweiten Newtonschen Gesetz
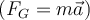 das Gewicht des Körpers
das Gewicht des Körpers 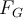 als Nettokraft und das der Schwerkraft
als Nettokraft und das der Schwerkraft 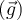 als die Beschleunigung verwenden, die es erhält, wird das Gewicht eines Körpers der Masse
als die Beschleunigung verwenden, die es erhält, wird das Gewicht eines Körpers der Masse 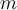 ausgedrückt durch:
ausgedrückt durch:Beachte, dass die Masse
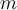 nicht vom Wert von
nicht vom Wert von 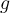 abhängt, aber das Gewicht
abhängt, aber das Gewicht 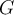 davon abhängt.
davon abhängt.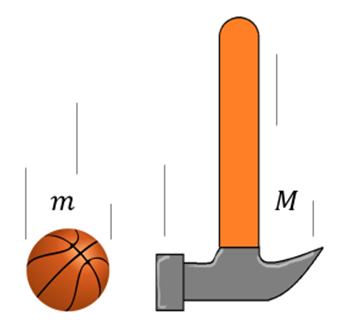
Gewicht und Masse von G. Jimenez - Masseneinheit: Das Kilogramm
Im internationalen Einheitensystem (SI) ist die Einheit der Beschleunigung
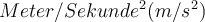 . Sowohl der Meter als auch die Sekunde sind Grundeinheiten. Die dritte Grundeinheit der Mechanik ist die Masse: das Kilogramm
. Sowohl der Meter als auch die Sekunde sind Grundeinheiten. Die dritte Grundeinheit der Mechanik ist die Masse: das Kilogramm 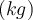 . Das Referenz-Standardkilogramm ist ein zylindrischer Barren aus Platin-Indium, der in Sevres, Frankreich, aufbewahrt wird.
. Das Referenz-Standardkilogramm ist ein zylindrischer Barren aus Platin-Indium, der in Sevres, Frankreich, aufbewahrt wird.- SI-Einheit der Kraft: Das Newton
Die SI-Einheit der Kraft ist das Newton
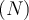 .
.Das Newton ist eine von den Grundeinheiten abgeleitete Einheit und nach dem zweiten Newtonschen Gesetz die Kraft, die auf eine Masse von 1 kg eine Beschleunigung von
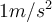 ausübt.
ausübt.Wenn wir Gewichte an das Ende einer Feder hängen, kann die Federdehnung erfasst werden, um Kräfte zu messen. Eine auf diese Weise kalibrierte Feder wird
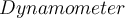 genannt. Dies ist das Arbeitsprinzip vieler Waagen.
genannt. Dies ist das Arbeitsprinzip vieler Waagen.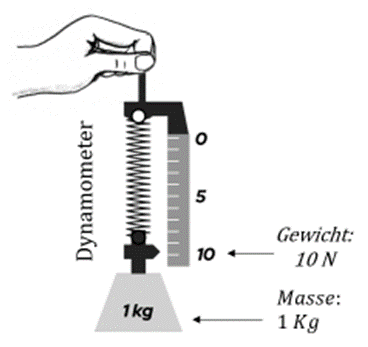
Newtonsche Einheit von N. Donner 💡 Tipp: Schau doch mal in diesem 👉 PepperMINT Modul 👈 vorbei, um mehr über das Thema Physikalischen Größen und Einheiten zu erfahren. -
Newtonsche Gesetze und Referenzrahmen
Der Charakter einer Bewegung ist vom gewählten Bezugsrahmen abhängig. Ein Körper könnte relativ zu einem Bezugssystem in Ruhe sein. Daher kann Newtons erstes Gesetz nicht gleichzeitig in mehreren Referenzrahmen gelten.Newtons erstes Gesetz definiert eine Art von Referenzrahmen, genannt Trägheitsreferenzrahmen, in dem ein Körper nicht beschleunigt, wenn er nicht gestört wird. In einem Inertialsystem - einem Bezugssystem in dem ein kräftefreier Körper sich entweder geradlinig-gleichförmig bewegt oder in Ruhe verharrt - ist die Beschleunigung eines Körpers das Ergebnis von Kräften, die von verschiedenen, identifizierbaren Ursprüngen/Ursachen ausgehen.
Problemlösungsstrategien
Die Lösung der Probleme in der Dynamik erfordert eine Reihe von Strategien, bei denen es notwendig sein kann, Intuition und Kreativität ins Spiel zu bringen. Begegnest du in der Schule oder im Studium solch einem Problem, so würde ich dir immer empfehlen, einen Aktionsplan zu befolgen, der in mehreren Phasen organisiert ist:
- Identifiziere den oder die zu analysierenden Körper und die Umgebung von jedem von ihnen (Oberflächen, Seiten, Federn und andere Körper)
- Isoliere jeden Körper und erstelle ein Diagramm, das alle auf ihn einwirkenden äußeren Kräfte zeigt. Dies ist ein sogenanntes Freikörperdiagramm.
Bei realen Objekten ist es wichtig, im Freikörperdiagramm anzugeben, wo die Kraftvektoren angreifen, da dies die Drehmomente dieser Kraft und die entsprechenden Drehungen bestimmt, die sie erzeugen können. In der Teilchendynamik interessiert uns jedoch nur die lineare Bewegung des Körpers, wir können seine Größe und Form ignorieren und ihn als Punktkörper betrachten. In diesem Fall wirken alle Kraftvektoren auf einen gemeinsamen Punkt.3. Wähle ein Trägheitsbezugssystem. Jeder Körper kann seine eigenen Koordinatenachsen mit geeignetem Ursprung und Orientierung haben.
4. Wende das zweite Newtonsche Gesetz auf orthogonale Komponenten auf jedes Freikörperdiagramm an.
5. Löse die Gleichungen nach den Unbekannten auf. Es müssen so viele Gleichungen wie Unbekannte vorhanden sein. Ersetze schließlich die numerischen Werte in den erhaltenen algebraischen Ausdrücken.
6. Sind die Ergebnisse angemessen? Es ist eine Frage, die wir uns immer wieder stellen müssen. Der Einsatz von Dimensionsanalysen kann als Lösungsprüfung sinnvoll sein. In vielen Fällen konnten die Vorhersagen der Lösung für Extremwerte der Variablen verifiziert werden. Dies würde es ermöglichen, etwaige Fehler oder Inkonsistenzen zu erkennen.
Freikörperdiagramm von G. Jimenez
-
Beispiele: Kraft und Bewegung
1) Eine Flugbegleiterin schiebt ihren Koffer mit der Masse
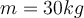 auf eine horizontale Fläche und zieht ihn am Riemen mit einer Kraft
auf eine horizontale Fläche und zieht ihn am Riemen mit einer Kraft 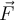 , die mit der Horizontalen einen Winkel
, die mit der Horizontalen einen Winkel 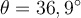 bildet. Die Reibung zwischen Koffer und Boden wird vernachlässigt.
bildet. Die Reibung zwischen Koffer und Boden wird vernachlässigt.- a) Wenn
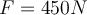 ist, wie groß ist dann die Beschleunigung des Koffers?
ist, wie groß ist dann die Beschleunigung des Koffers? - b) Welche Normalkraft übt der Boden auf den Koffer aus?
- c) Angenommen, der Wert der Kraft wird allmählich erhöht: Bei welchem Wert von F verliert der Koffer den Bodenkontakt?
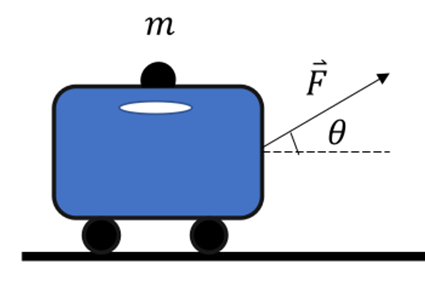
Lösung:
a) Die auf den Koffer wirkenden Kräfte sind im Freikörperbild dargestellt. Zu der auf den Riemen wirkenden Kraft
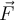 kommen hinzu: die Gewichtskraft
kommen hinzu: die Gewichtskraft 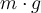 und die vom Boden ausgeübten Normalkräfte auf jedes der vier Räder. Wir haben dies durch einen Vektor
und die vom Boden ausgeübten Normalkräfte auf jedes der vier Räder. Wir haben dies durch einen Vektor 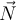 dargestellt. Wir können das zweite Newtonsche Gesetz in Form von kartesischen Komponenten anwenden.
dargestellt. Wir können das zweite Newtonsche Gesetz in Form von kartesischen Komponenten anwenden.
Aus der ersten Gleichung folgt, die Beschleunigung in horizontaler Richtung beträgt: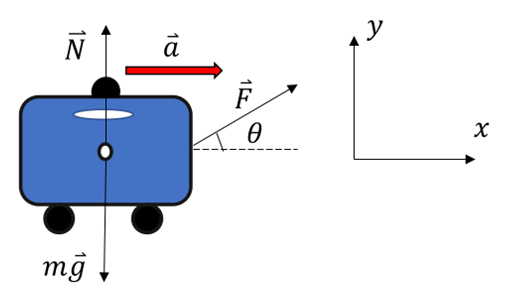
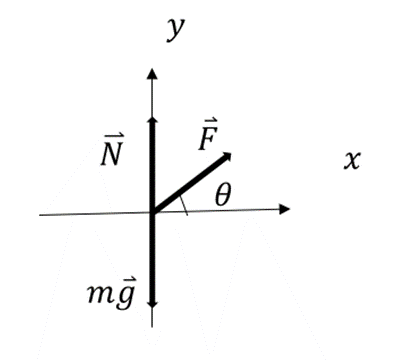
b) Der Wert der Normalkraft ergibt sich aus der zweiten Gleichung: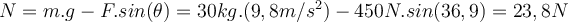
c) Wenn die Größe der angelegten Kraft erhöht wird, behält der Koffer den Kontakt bei, solange die Normalkraft positiv bleibt
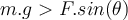 . Der kritische Wert von
. Der kritische Wert von 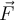 entspricht
entspricht 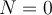 .
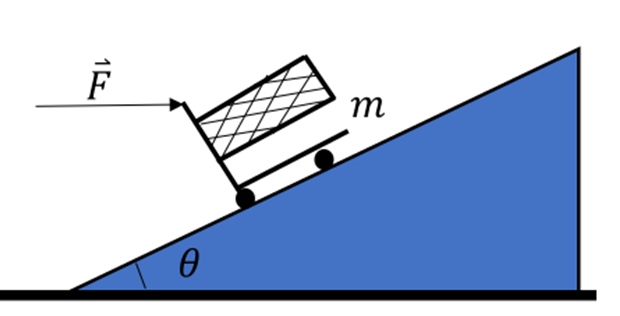
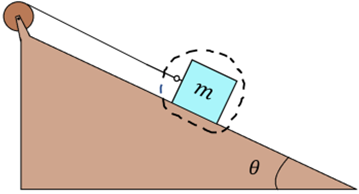
.2) Eine Person übt eine horizontale Kraft
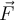 aus, um einen Einkaufswagen eine Rampe mit einem Neigungswinkel
aus, um einen Einkaufswagen eine Rampe mit einem Neigungswinkel 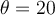 hinaufzuschieben. Die Gesamtmasse des Wagens mit der Ladung beträgt
hinaufzuschieben. Die Gesamtmasse des Wagens mit der Ladung beträgt 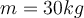 und die Reibung zwischen dem Wagen und der Rampenoberfläche wird vernachlässigt.
und die Reibung zwischen dem Wagen und der Rampenoberfläche wird vernachlässigt.- a) Berechne die Kraft, um den Wagen in Ruhe zu halten.
- b) Wenn eine Kraft F aufgebracht wird, die den doppelten Wert hat, bestimme die Beschleunigung des Wagens.
Lösung:
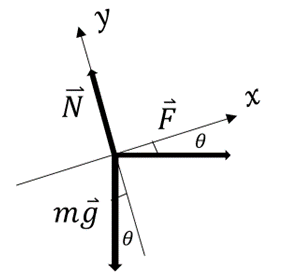
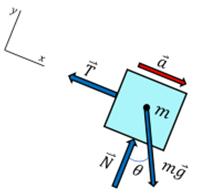
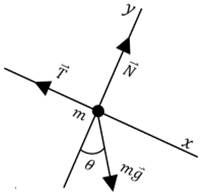
a) Zuerst zeichnen wir das Freikörperbild für den Wagen. Es gibt drei Kräfte: das senkrecht nach unten wirkende Gewicht m.g, die von der Person aufgebrachte Horizontalkraft
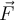 und die senkrecht zur Ebene wirkende Normalkraft. Bei solchen Problemen mit schiefen Ebenen ist es zweckmäßig, Koordinatenachsen mit
und die senkrecht zur Ebene wirkende Normalkraft. Bei solchen Problemen mit schiefen Ebenen ist es zweckmäßig, Koordinatenachsen mit 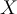 entlang der Neigung und
entlang der Neigung und 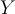 senkrecht dazu zu wählen. Auf diese Weise hätte die Beschleunigung eine einzige Komponente. Wenn der Wagen ruht, ist seine Beschleunigung Null und die Anwendung des zweiten Newtonschen Gesetzes in Komponentenform ergibt:
senkrecht dazu zu wählen. Auf diese Weise hätte die Beschleunigung eine einzige Komponente. Wenn der Wagen ruht, ist seine Beschleunigung Null und die Anwendung des zweiten Newtonschen Gesetzes in Komponentenform ergibt:
Aus Gleichung (1) wird die Kraft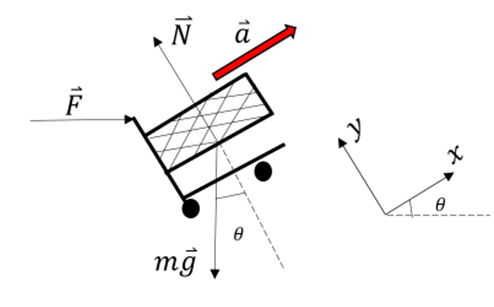
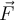 errechnet:
errechnet:
b) Wenn der Wert von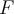 erhöht wird, erhält der Wagen eine Beschleunigung entlang der Neigung (x-Achse ) und wir erhalten:
erhöht wird, erhält der Wagen eine Beschleunigung entlang der Neigung (x-Achse ) und wir erhalten:Beim Lösen erhalten wir die Beschleunigung:
3) Im Studentenwohnheim bricht ein Feuer aus und eine Studentin rettet sich mit einem Seil. Nachdem sie ein Ende des Seils an ein Bett gebunden hat, beginnt sie durch das Fenster abzusteigen, indem die Studentin an dem Seil herunterrutscht. Die Studentin hat ein Gewicht von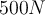 , aber die maximale Spannung, der das Seil standhalten kann, beträgt
, aber die maximale Spannung, der das Seil standhalten kann, beträgt 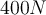 . Wie soll die Studentin herunterkommen, ohne dass das Seil reißt?
. Wie soll die Studentin herunterkommen, ohne dass das Seil reißt?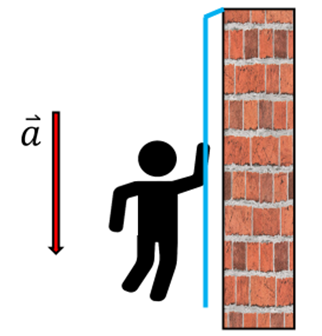
Lösung: Wenn die Studentin das Seil nach unten zieht, zieht das Seil diese nach dem dritten Newtonschen Gesetz mit einer gleich großen Kraft
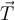 nach oben. Auf dem Freikörperbild sind die beiden auf die Studentin einwirkenden Kräfte eingezeichnet: wenn das Gewicht m.g nach unten und die Spannung in dem Seils
nach oben. Auf dem Freikörperbild sind die beiden auf die Studentin einwirkenden Kräfte eingezeichnet: wenn das Gewicht m.g nach unten und die Spannung in dem Seils 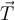 . nach oben zeigt.
. nach oben zeigt.Wenn die Studentin versucht, sehr langsam (fast in Ruhe) nach unten zu gehen, würde die Spannung im Seil, die ihr Gewicht ausgleichen würde, etwa
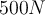 betragen und das Seil würde sofort reißen. Daher muss sie beschleunigt gleiten, damit die Spannung im Seil den Grenzwert von
betragen und das Seil würde sofort reißen. Daher muss sie beschleunigt gleiten, damit die Spannung im Seil den Grenzwert von 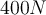 nicht überschreiten kann. Die Anwendung des zweiten Newtonschen Gesetzes ergibt:
nicht überschreiten kann. Die Anwendung des zweiten Newtonschen Gesetzes ergibt: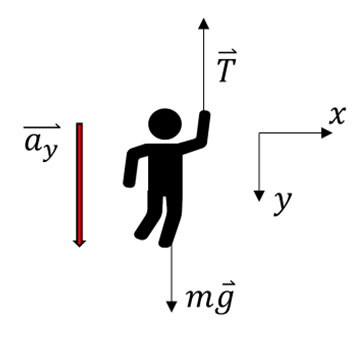
Wenn wir nach
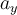 auflösen, erhalten wir:
auflösen, erhalten wir:Daher muss die minimale Abstiegsbeschleunigung sein:
4) Zwischen zwei auf gleicher Höhe befindlichen Fixpunkten ist eine flexible Kette
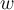 aufgehängt. Die Form der Kurve, die sie annimmt, wird als Kettenlinie bezeichnet. An den äußersten Punkten der Aufhängung
aufgehängt. Die Form der Kurve, die sie annimmt, wird als Kettenlinie bezeichnet. An den äußersten Punkten der Aufhängung 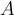 und
und 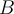 bildet die Kette einen Winkel
bildet die Kette einen Winkel 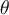 mit der Horizontalen.
mit der Horizontalen.- a) Finde die Spannung der Kette in ihrem Mittelpunkt.
- b) Finde die Kraft, die jede Stütze auf die Enden der Kette ausübt.
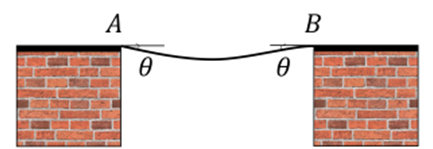
Lösung:
a) Wir zeichnen das Freikörperbild für eine Hälfte der Kette.
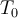 sei die Kettenspannung am tiefsten Punkt,
sei die Kettenspannung am tiefsten Punkt, 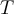 die Spannung am Stützpunkt und
die Spannung am Stützpunkt und 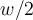 das Gewicht der halben Kette, das auf ihren Schwerpunkt wirkt.
das Gewicht der halben Kette, das auf ihren Schwerpunkt wirkt.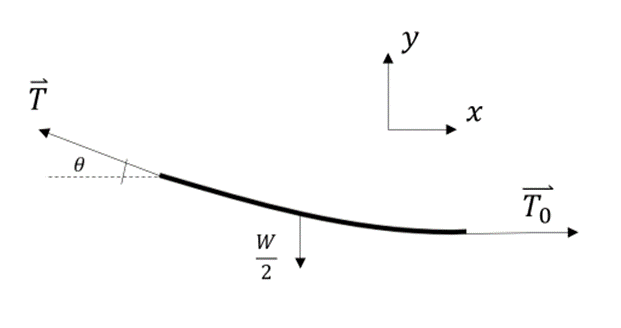
Die Translationsgleichgewichtsgleichungen lauten:
Wenn wir diese beiden Gleichungen dividieren, erhalten wir die Spannung am Mittelpunkt der Kette:
b) Setzen wir nun T_0 in Gleichung (1) ein, so erhalten wir die Spannung in den Stützpunkten:
5) Eine
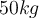 schwere Person steht auf einer Waage in einem Aufzug. Die Skala ist in Newton eingestellt. Was wird die Skala in den folgenden Fällen anzeigen?
schwere Person steht auf einer Waage in einem Aufzug. Die Skala ist in Newton eingestellt. Was wird die Skala in den folgenden Fällen anzeigen?- a) Der Aufzug fährt mit konstanter Geschwindigkeit nach oben oder unten.
- b) Der Aufzug fährt mit einer Beschleunigung
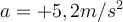 nach oben
nach oben - c) Der Aufzug fährt mit einer Beschleunigung
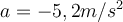 nach unten
nach unten - d) Wenn die Aufzugseile reißen.

Lösung:
Wir wählen einen Trägheitsbezugsrahmen außerhalb des Aufzugs (fest am Boden). Die auf die Person wirkenden Kräfte sind: die von der Waage ausgeübte Kraft
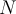 (Waagenanzeige) und das wahre Gewicht.
(Waagenanzeige) und das wahre Gewicht. 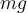 . Wenn wir die positive Richtung nach oben wählen und das zweite Newtonsche Gesetz anwenden, haben wir:
. Wenn wir die positive Richtung nach oben wählen und das zweite Newtonsche Gesetz anwenden, haben wir: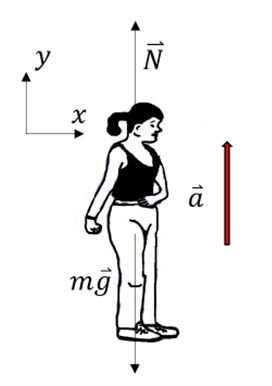
a) Wenn die Geschwindigkeit des Aufzugs konstant ist (
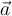 ist Null), ist das scheinbare Gewicht der Person gleich ihrem wahren Gewicht.
ist Null), ist das scheinbare Gewicht der Person gleich ihrem wahren Gewicht.b) Wenn der Aufzug nach oben beschleunigt
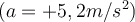 , ist das scheinbare Gewicht der Person größer als das wahre Gewicht:
, ist das scheinbare Gewicht der Person größer als das wahre Gewicht:c) Wenn der Aufzug nach unten beschleunigt
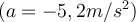 , ist das scheinbare Gewicht der Person geringer als ihr wahres Gewicht:
, ist das scheinbare Gewicht der Person geringer als ihr wahres Gewicht:Diese Effekte werden von der Person als Zunahme oder Abnahme des Aufwärtsschubs empfunden, den ihre Füße erhalten. Beachte, dass es auf die Richtung der Beschleunigung in Bezug auf die Bewegungsrichtung des Aufzugs ankommt. Dabei spielt es keine Rolle, ob der Aufzug nach oben oder nach unten fährt.
d) Wenn die Aufzugseile reißen, die den Aufzug tragen, fallen sowohl der Aufzug als auch die Person frei
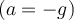 und es gibt keine Normalkraft
und es gibt keine Normalkraft 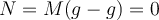 . Das heißt, das scheinbare Gewicht wird Null sein.
. Das heißt, das scheinbare Gewicht wird Null sein. - a) Wenn
-
Anwendungen der Newtonschen Gesetze
Die grundlegenden Wechselwirkungen
In der Natur finden wir verschiedene Arten von Kräften. Letztendlich resultieren diese aus vier grundlegenden Wechselwirkungen:
- Gravitationswechselwirkung: Sie hängt mit einer Eigenschaft der Materie zusammen, die „Masse“ genannt wird, und manifestiert sich in der gegenseitigen Anziehung zwischen allen Körpern.
- Elektromagnetische Wechselwirkung: Sie manifestiert sich als Anziehung oder Abstoßung zwischen Teilchen mit "elektrischer Ladung". Die elektromagnetische Wechselwirkung ist dafür verantwortlich, Atome und Moleküle in der Materie zusammenzuhalten.
- Schwache Wechselwirkung: Sie äußert sich in bestimmten Prozessen des radioaktiven Zerfalls und in Reaktionen zwischen Elementarteilchen.
- Starke Wechselwirkung: Das ist die Art von Kraft, die die Bestandteile der Atomkerne, Protonen und Neutronen, sowie die Quarks innerhalb dieser Teilchen zusammenhält.
Die Gravitationskraft/ Schwerkraft.
Die Erdanziehungskraft, die von der Erde auf den Mond und die künstlichen Satelliten ausgeübt wird, ist dafür verantwortlich, dass sie in der Umlaufbahn um ihn herum gehalten werden. Betrachtet man die Erde als gleichförmige Kugel der Masse
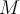 und
des Radius
und
des Radius 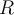 , so ist die Anziehungskraft, die sie auf ein Objekt der Masse
, so ist die Anziehungskraft, die sie auf ein Objekt der Masse 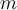 in der Höhe
in der Höhe 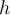 auf ihrer Oberfläche ausübt:
auf ihrer Oberfläche ausübt: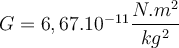 , die universelle Gravitationskonstante. In Bezug auf die Erdbeschleunigung
, die universelle Gravitationskonstante. In Bezug auf die ErdbeschleunigungDie Schwerkraft ist für das Gewicht von Körpern verantwortlich. Wendet man das zweite Newtonsche Gesetz
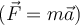 auf den frei fallenden Körper der Masse
auf den frei fallenden Körper der Masse 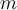 an, so kann man schlussfolgern dass aus
an, so kann man schlussfolgern dass aus 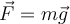 ,
, 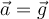 folgt. Mit anderen Worten, am gleichen Ort auf der Erde fallen alle Körper unabhängig von ihrer Masse mit der gleichen Beschleunigung.
folgt. Mit anderen Worten, am gleichen Ort auf der Erde fallen alle Körper unabhängig von ihrer Masse mit der gleichen Beschleunigung.Mit Ausnahme der irdischen Schwerkraft sind alle Kräfte in unserer makroskopischen Umgebung im Wesentlichen elektromagnetischen Ursprungs. Diese Kräfte werden auf mikroskopischer Ebene zwischen den Materieatomen erzeugt. Die elastischen Kräfte von Federn, die Spannung eines Seils und die Kontaktkräfte zwischen Objekten wie Reibungs- und Adhäsionskräfte sind elektrischer Art.
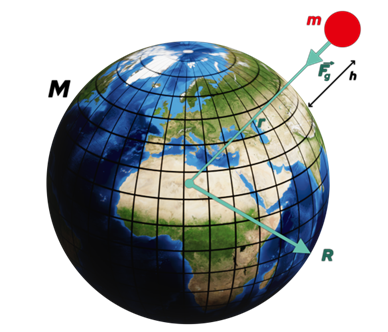
Gra  vitationskraft von N. Donner
vitationskraft von N. DonnerKontaktkräfte
Beim Kontakt von Objekten wirken durch die Wechselwirkung der Moleküle des einen Körpers mit denen des anderen Körpers Kräfte aufeinander ein. Die sogenannte Kontaktkraft hat im Allgemeinen zwei Komponenten:
- Eine Komponente senkrecht zur Oberfläche, die Normalkraft
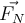 genannt wird
genannt wird - und eine tangentiale Komponente
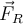 , die Reibungskraft
genannt wird.
, die Reibungskraft
genannt wird.
Die Normalkraft tritt immer dann auf, wenn ein Körper gegen eine Oberfläche gedrückt wird. Diese Kraft gleicht die Kraft aus, die den Körper durch die Oberfläche hindurch beschleunigen würde, und verhindert, dass die beiden Materialien ineinander eindringen.Die Reibungskoeffizienten hängen von der Beschaffenheit der Oberflächen ab. Der Haftreibungskoeffizient
Die tangentiale Reibungskraft ist auf molekulare Wechselwirkungen zurückzuführen, die zwischen eng aneinander liegenden Oberflächen wirken (Adhäsion) und auf die Rauheit der Flächen.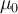 ist immer größer als der Gleitreibungskoeffizient
ist immer größer als der Gleitreibungskoeffizient 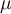 . Ihre Werte werden experimentell ermittelt. Die Ungleichheit kommt daher, dass ein ruhender Körper erst einmal "losgerissen" werden muss und dann etwas einfacher in Bewegung zu halten ist.
. Ihre Werte werden experimentell ermittelt. Die Ungleichheit kommt daher, dass ein ruhender Körper erst einmal "losgerissen" werden muss und dann etwas einfacher in Bewegung zu halten ist.
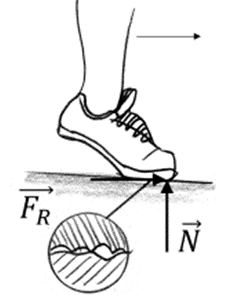
Kontaktkräfte von N. Donner Komponenten der vom Untergrund auf den Schuh ausgeübten Kraft. Die Reibungskraft verhindert, dass der Schuh nach hinten rutscht.Statische Reibung
Angenommen, wir versuchen ein Objekt auf einer horizontalen Oberfläche zu verschieben, indem wir eine kleine Kraft
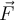 anwenden. Zunächst verhindert die Reibungskraft
anwenden. Zunächst verhindert die Reibungskraft 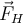 eine Relativbewegung
und wir haben den statischen Fall. Wenn wir die aufgebrachte Kraft erhöhen, steigt auch die Haftreibungskraft, und wenn wir das Objekt nicht bewegen können, liegt das daran, dass sich diese Kraft
auf den geeigneten Wert anpasst, um das Gleichgewicht zu halten.
eine Relativbewegung
und wir haben den statischen Fall. Wenn wir die aufgebrachte Kraft erhöhen, steigt auch die Haftreibungskraft, und wenn wir das Objekt nicht bewegen können, liegt das daran, dass sich diese Kraft
auf den geeigneten Wert anpasst, um das Gleichgewicht zu halten.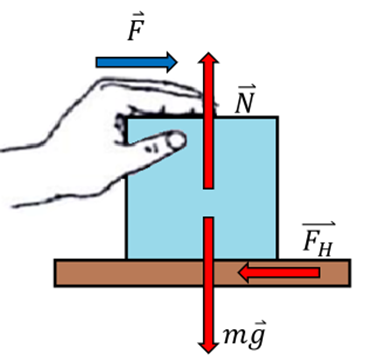
Statische Riebung von G. Jimenez
Schließlich erreicht die Haftreibungskraft einen maximalen Wert, und wenn dies geschieht, droht das Objekt zu rutschen. Der von der Haftreibungskraft erreichte Maximalwertist proportionalzum Wert der Normalkraft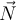 .
.
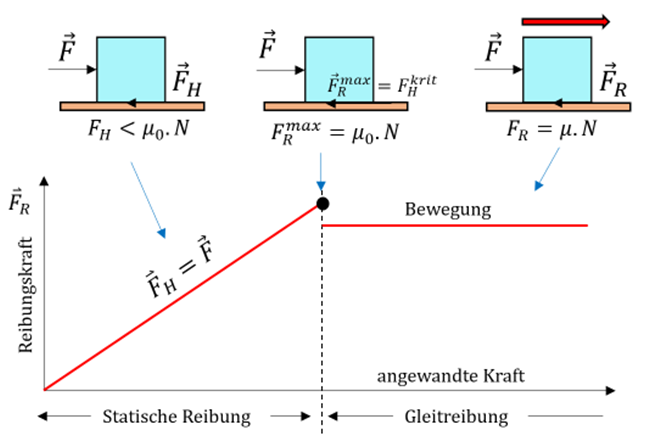
Grafische Darstellung der Reibungskraft. von G. Jimenez 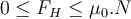
Gleitreibung
Wenn die aufgebrachte Kraft groß genug ist, um die Haftreibung zu überwinden, tritt "Schlupf" auf: Sobald das Objekt gleitet, gibt es eine kinetische Reibungskraft
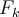 , die der relativen Bewegung zwischen den beiden
Oberflächen entgegenwirkt. Ihr Wert ist proportional zur Normalkraft
, die der relativen Bewegung zwischen den beiden
Oberflächen entgegenwirkt. Ihr Wert ist proportional zur Normalkraft 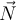 .
.Die Reibungskoeffizienten hängen von der Art der Kontaktflächen ab und sind
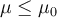 . Diese sind nahezu unabhängig von der Kontaktfläche zwischen den Oberflächen.
. Diese sind nahezu unabhängig von der Kontaktfläche zwischen den Oberflächen.Elastische Kräfte: Federn
Wenn eine Feder gestaucht oder gedehnt wird, übt sie eine Kraft aus, die von der entsprechenden Verformung abhängt. Wird die Feder dann entspannt, nimmt sie ihre ursprüngliche Länge wieder an, sofern die Verformung einen bestimmten Grenzwert nicht überschreitet. Jenseits dieser Grenze wird die Feder dauerhaft verformt. Für Dehnungen unterhalb dieser Grenze gehorcht die Feder dem Hookeschen Gesetz.Dabei ist (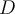 oder
oder 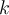 ) die elastische Konstante (Federkonstate) der Feder und (
) die elastische Konstante (Federkonstate) der Feder und ( 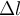 oder
oder 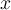 ) die Verschiebung des freien Endes der Feder in Bezug auf ihre Gleichgewichtsposition (die Dehnung).
) die Verschiebung des freien Endes der Feder in Bezug auf ihre Gleichgewichtsposition (die Dehnung).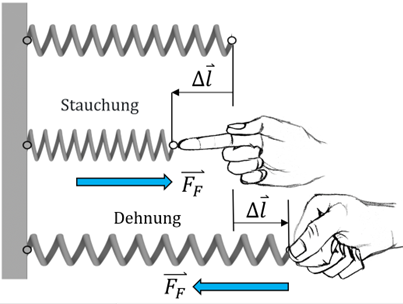
Hookesches Gesetz. von G. Jimenez Der nachfolgende Link führt zu einer externen Internetseite, die ggf. andere Datenschutzvorgaben erfüllt als wir es auf dieser Plattform tun. Dabei können Daten von dir übertragen und weiterverarbeitet werden. Wenn du dich allgemein zum Thema Datenschutz erkundigen möchtest, empfehlen wir dir die Erklärvideos der Initiative Datenschutz geht zur Schule.Klicke 👉hier, um auf die Simulation über das Hookesche Gesetz zuzugreifen 😀 🏃💨
Probiere in der Einführung einmal aus,, wie die Kraft von der Auslenkung der Feder abhängt. Prüfe und sieh interaktiv, wie groß die Rückstellkraft der Feder ist, die Wirkrichtung und die Gleichgewichtslage des Systems. In weiteren Modulen beschäftigen wir uns mit Federsystemen und Energie.Federsysteme- Reihenschaltung von Federn:
Wenn Federn in Reihe geschaltet sind, bedeutet dies, dass zwei oder mehr Federn Rücken an Rücken (in einer Reihe) verbunden sind. Hier wird eine Angriffskraft nicht wie bei der Parallelschaltung verteilt, sondern wirkt durch alle Federn in gleicher Höhe. Bei Reihenschaltung können die Federn unterschiedliche Federkonstanten und unterschiedliche Längen aufweisen, was sich entsprechend auf die Gesamtlängenänderung auswirkt.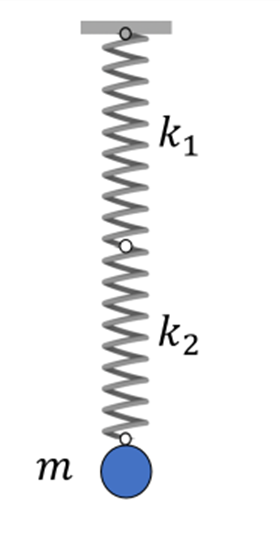
Reihenschaltung von Federn. G.Jimenez Um die Ersatzfederkonstante zu berechnen, verwenden wir die folgende Formel:- Parallelschaltung von Federn:
Parallelschaltung bedeutet, dass zwei oder mehr Federn nebeneinander wirken. Auf diese Weise wird eine Angriffskraft auf alle Federn verteilt. Diese Federn können unterschiedliche Federkonstanten und unterschiedliche Längen haben.Parallel geschaltete Federn werden durch Addition der Federkonstanten berechnet, wodurch eine sogenannte Ersatzfeder mit einer äquivalenten Federkonstante (bzw. der resultierenden Federkonstante) entsteht. Da die Federn nebeneinander wirken und die Kraft verteilt wird, ergibt sich im Prinzip eine stärkere/härtere Gesamtfeder. Richtig ist hier allerdings der Begriff Ersatzfeder, da die Summe aller Federn als eine betrachtet wird.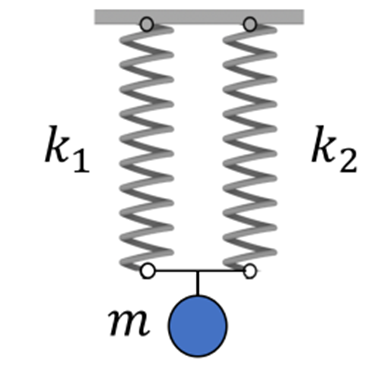
Parallelschaltung von Federn. G.Jimenez Um die Ersatzfederkonstante zu berechnen, verwenden wir die folgende Formel: -
Dynamik der Kreisbewegung
Stellen wir uns ein Objekt vor, das sich auf einem Kreis mit dem Radius
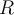 mit konstanter Geschwindigkeit
mit konstanter Geschwindigkeit 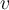 bewegt (gleichförmige Kreisbewegung). Da der Vektor
bewegt (gleichförmige Kreisbewegung). Da der Vektor 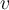 die Richtung ändert, sagen wir, dass das Objekt eine Beschleunigung
die Richtung ändert, sagen wir, dass das Objekt eine Beschleunigung 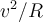 erfährt und auf das Rotationszentrum gerichtet ist (Zentripetalbeschleunigung). Nach Newtons zweitem Gesetz gilt:
erfährt und auf das Rotationszentrum gerichtet ist (Zentripetalbeschleunigung). Nach Newtons zweitem Gesetz gilt: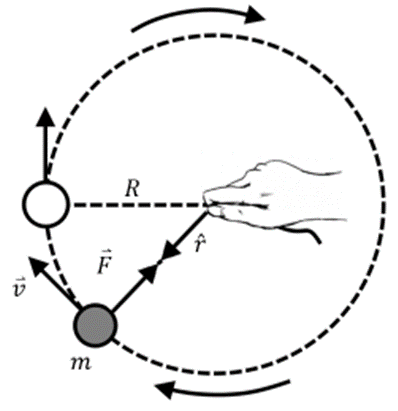
Dynamik der Kreisbewegung von G. Jimenez Ungleichmäßige Kreisbewegung
Wenn die auf ein rotierendes Objekt ausgeübte Kraft nicht auf den Kreismittelpunkt gerichtet ist, sondern mit der radialen Linie einen Winkel bildet, hat die Beschleunigung des Teilchens zwei Komponenten, eine radiale und eine tangentiale.
Die tangentiale Komponente der Kraft wirkt, um den Geschwindigkeitsmodul zu erhöhen oder zu verringern und verursacht eine tangentiale Beschleunigung:
Die radiale Komponente bewirkt die Richtungsänderung des Geschwindigkeitsvektors:
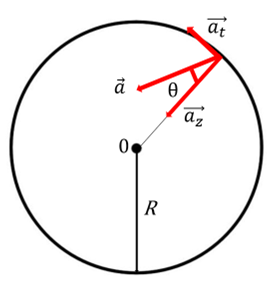
Ungleichförmiger Kreisbewegung von G. Jimenez Kräfte in beschleunigten Systemen
Die Newtonschen Gesetze gelten nur für Inertialbeobachter. Angenommen, eine Schülerin steigt mit einem Koffer auf Rädern in den Zug. Wenn der Zug mit einer Beschleunigung
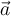 anfährt, bemerkt der Inertialbeobachter am Bahnsteig,
anfährt, bemerkt der Inertialbeobachter am Bahnsteig,  , dass sich der Koffer im Vergleich zu ihm „nicht bewegt“ und schließt daraus, dass keine Nettokraft auf ihn einwirkt, wie durch das erste Newtonsche Gesetz festgelegt.
, dass sich der Koffer im Vergleich zu ihm „nicht bewegt“ und schließt daraus, dass keine Nettokraft auf ihn einwirkt, wie durch das erste Newtonsche Gesetz festgelegt.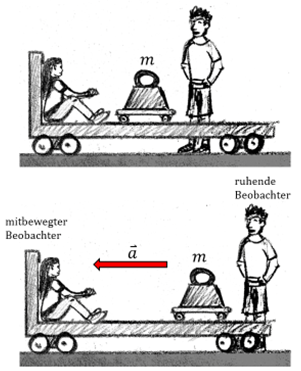
Kräfte in beschleunigten Systemen. G. Jimenez
Die im Zug sitzende, nicht-inertiale Beobachterin (mitbewegte Beobachterin) teilt die Meinung, dass keine Nettokraft auf den Koffer wirkt, aber beobachtet dennoch mit Erstaunen, dass ihr Koffer von ihr wegrollt. Daher muss die mitbewegte Beobachterin, wenn sie den Konflikt mit Newtons zweitem Gesetz überwinden will, unbedingt davon ausgehen, dass irgendeine mysteriöse, nach hinten gerichtete Kraft auf den Koffer wirkt.
Diese Kraft wird als Trägheitskraft oder Pseudokraft bezeichnet, da ihre Existenz ausschließlich von der Bewegung des Beobachters abhängt und mit keinem Wechselwirkungsmechanismus verbunden ist. Das heißt, die Kraft wird nicht von einem externen Verursacher ausgeübt und entspricht daher nicht dem dritten Newtonschen Gesetz.
Diese Kräfte in beschleunigenden Rahmen werden auch als fiktive Kräfte bezeichnet, sind aber in ihrer Wirkung genauso real wie die Schwerkraft.
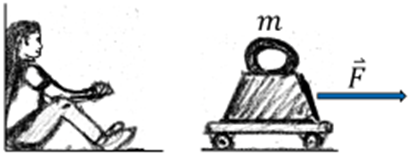
mitbewegter Beobachter. G. Jimenez Pseudokräfte gehorchen nicht dem 3. Gesetz von Newton.
Laut nicht-Inertialbeobachter (mitbewegter Beobachter) gibt es eine Pseudokraft: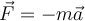
Pseudokräfte in rotierenden Rahmen
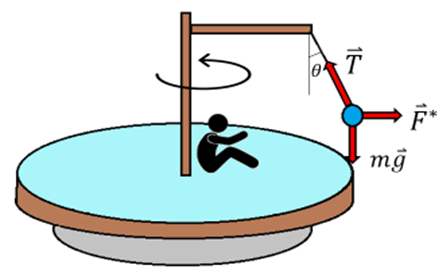
Die Abbildung zeigt eine Kugel der Masse m, die an einer Schnur aufgehängt und an einer Plattform befestigt ist, die sich mit der Winkelgeschwindigkeit
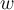 dreht. Ein außerhalb befindlicher Inertialbeobachter (ruhender Beobachter) sieht, wie die Kugel mit der Winkelgeschwindigkeit
dreht. Ein außerhalb befindlicher Inertialbeobachter (ruhender Beobachter) sieht, wie die Kugel mit der Winkelgeschwindigkeit 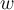 einen Umfang vom Radius
einen Umfang vom Radius 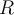 beschreibt. Er erklärt seine Beobachtung damit, dass die kleine Kugel zum Mittelpunkt des Umfangs hin beschleunigt wird und ihre Zentripetalbeschleunigung
beschreibt. Er erklärt seine Beobachtung damit, dass die kleine Kugel zum Mittelpunkt des Umfangs hin beschleunigt wird und ihre Zentripetalbeschleunigung 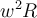 auf eine unausgeglichene zentripetale (nach innen gerichtete) Kraft zurückzuführen ist, die in diesem Fall die horizontale Komponente der Spannung in der Schnur ist . . .
auf eine unausgeglichene zentripetale (nach innen gerichtete) Kraft zurückzuführen ist, die in diesem Fall die horizontale Komponente der Spannung in der Schnur ist . . .Der mit der Plattform rotierende nicht-Inertialbeobachter (mitbewegter Beobachter) interpretiert das Phänomen auf andere Weise. Ihm zufolge ruht die kleine Kugel und beschleunigt nicht. Er besteht darauf, Newtons 2. Gesetz anzuwenden, und da es keinen identifizierbaren Akteur gibt, der die Kugel nach außen drückt, hält er es für notwendig, eine Pseudokraft der Größe
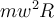 zu erfinden, die radial „nach außen“ wirkt. Diese Trägheitskraft gleicht die horizontale Komponente der Schnuspannung aus, sodass die Nettokraft auf die Kugel Null ist.
zu erfinden, die radial „nach außen“ wirkt. Diese Trägheitskraft gleicht die horizontale Komponente der Schnuspannung aus, sodass die Nettokraft auf die Kugel Null ist.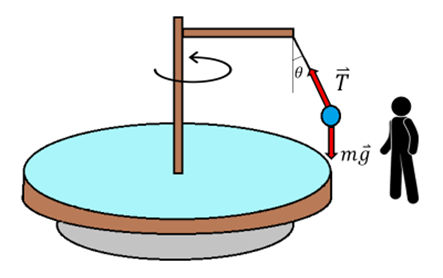
Inertialbeobachter von G. Jimenez Die Pseudokraft, die von einem mitrotierendem Beobachter wahrgenommen wird, wird als Zentrifugalkraft (nach außen) bezeichnet. Diese Art von Kraft ist jedem wohlbekannt, denn wir fühlen zum Beispiel, wenn wir in einem Auto um die Kurve fahren, eine Art unsichtbare Hand, die uns nach außen drückt.
Es ist wichtig klarzustellen, dass für Inertial Beobachter niemals Zentrifugalkraft vorhanden ist. Von außen betrachtet liefert die Reibung zwischen Reifen und Fahrbahn die Zentripetalkraft, die das Auto selbst beschleunigt. Die zentripetale Normalkraft der Autotür drückt den Passagier und zwingt ihn, sich auf der gekrümmten Bahn zu bewegen.
nicht-Inertialer Beobachter von G. Jimenez Corioliskraft
Schließlich müssen wir erwähnen, dass, wenn sich ein Objekt in Bezug auf ein rotierendes Bezugssystem bewegt, zusätzlich zur Zentrifugalkraft eine zweite Pseudokraft auftritt, die Corioliskraft genannt wird, die rechtwinklig zum Geschwindigkeitsvektor wirkt.
Widerstandskräfte in einer Flüssigkeit
Viskose Widerstandskräfte können zwischen einer Flüssigkeit (Flüssigkeit oder Gas) und einem Festkörper mit Bewegung relativ zur Flüssigkeit und auch zwischen Teilchen derselben Flüssigkeit entstehen. Ein Körper, der sich durch eine Flüssigkeit bewegt, erfährt eine Widerstandskraft, die von der Form des Körpers und den Eigenschaften des Mediums abhängt, in dem er sich bewegt. Im Allgemeinen nimmt diese Kraft mit der Geschwindigkeit zu. Wenn ein Körper in eine Flüssigkeit fällt, wirkt die Widerstandskraft in die entgegengesetzte Richtung zur Bewegung, und wenn sie gleich dem Gewicht des fallenden Körpers wird, erreicht sie ihre maximale oder Endgeschwindigkeit.
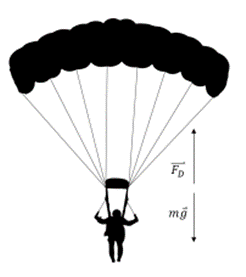
Widerstandskraft von G. Jimenez
-
Beispiele: Anwendungen der Newtonschen Gesetze
1) Eine Flasche der Masse
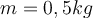 wird mit einer Anfangsgeschwindigkeit
wird mit einer Anfangsgeschwindigkeit 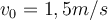 horizontal über eine Tischfläche nach rechts geschubst. Die Flasche gleitet in einer geraden Linie und verlangsamt sich über eine gewisse Strecke
horizontal über eine Tischfläche nach rechts geschubst. Die Flasche gleitet in einer geraden Linie und verlangsamt sich über eine gewisse Strecke 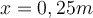 , bevor sie zum Stillstand kommt. Unter der Annahme, dass die Reibungskraft konstant bleibt, wie groß ist der kinetische Reibungskoeffizient zwischen der Flasche und dem Tisch?.
, bevor sie zum Stillstand kommt. Unter der Annahme, dass die Reibungskraft konstant bleibt, wie groß ist der kinetische Reibungskoeffizient zwischen der Flasche und dem Tisch?.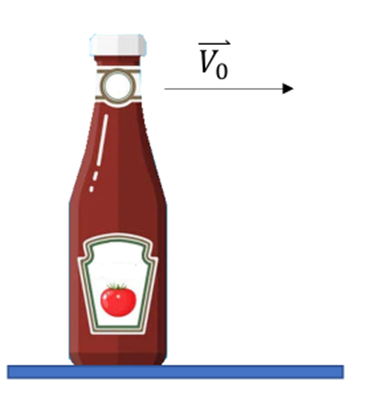
Lösung:
Sobald die Flasche geschubst wird, wirken auf sie folgende Kräfte: ihr Gewicht
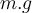 , die vom Tisch ausgeübte Normalkraft
, die vom Tisch ausgeübte Normalkraft 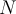 und die kinetische Reibungskraft
und die kinetische Reibungskraft 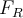 , die eine horizontale Verzögerung erzeugt.
, die eine horizontale Verzögerung erzeugt.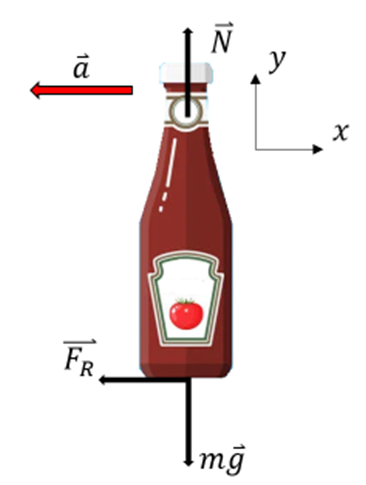
Anwendung des zweiten Newtonschen Gesetzes in Komponentenform:
Daher ist die Beschleunigung:
Da die Beschleunigung konstant ist, können wir die Kinematikgleichung mit Endgeschwindigkeit Null verwenden:
Daher ist der kinetische Reibungskoeffizient zwischen der Flasche und dem Tisch: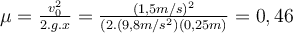
2) Ein Block der Masse
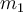 wird auf einen anderen Block der Masse
wird auf einen anderen Block der Masse 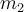 gelegt, der wiederum auf einer glatten horizontalen Oberfläche ruht. Auf den Block
gelegt, der wiederum auf einer glatten horizontalen Oberfläche ruht. Auf den Block 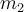 wird eine horizontale Kraft
wird eine horizontale Kraft 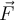 ausgeübt. Finde die Beschleunigung jedes Blocks in den folgenden Fällen:
ausgeübt. Finde die Beschleunigung jedes Blocks in den folgenden Fällen:- a) Wenn es keine Reibung zwischen den Blöcken gibt.
- b) Wenn die Oberflächen zwischen den Blöcken rau genug sind, um sicherzustellen, dass
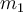 nicht über
nicht über 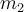 rutscht.
rutscht. - c) Wenn der obere Block auf dem unteren gleitet aufgrund des Einflusses der kinetischen Reibung mit dem Koeffizienten
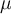 .
.
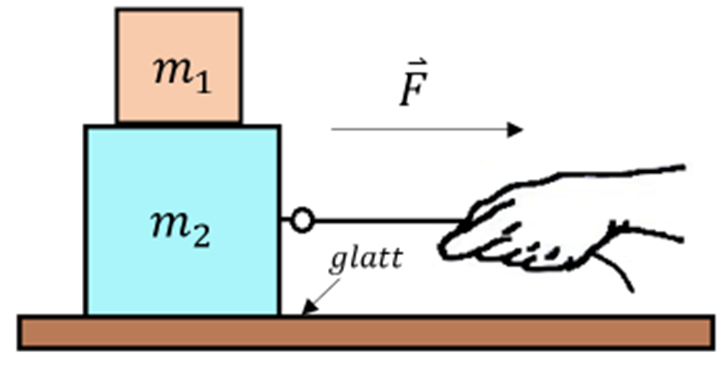
Lösung:
a) Wenn es keine Reibung gibt, wird keine horizontale Kraft auf den Block
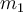 ausgeübt und seine Beschleunigung wird Null sein
ausgeübt und seine Beschleunigung wird Null sein 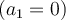 . Auf den Block
. Auf den Block 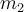 wird eine Nettokraft F ausgeübt. Die Beschleunigung beträgt:
wird eine Nettokraft F ausgeübt. Die Beschleunigung beträgt:b) Wenn genügend Reibung zwischen den Blöcken vorhanden ist, bewegen sie sich zusammen. Anwendung des 2. Newtonschen Gesetzes auf die kombinierte Masse:
c) Wenden wir Newtons 2. Gesetz auf jeden Block an, haben wir:
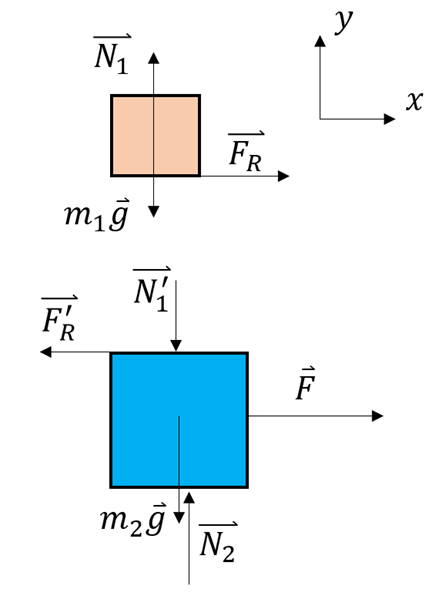
Wenn wir die Gleichungen (1) und (2) kombinieren, finden wir
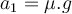
Unter Berücksichtigung, dass die kinetische Reibungskraft, die den Block
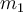 drückt,
drückt, 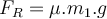 ist, haben wir:
ist, haben wir:3) Ein Block der Masse
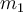 wird auf einen Block der Masse
wird auf einen Block der Masse 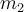 gelegt. Auf Block
gelegt. Auf Block 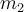 wird eine horizontale Kraft
wird eine horizontale Kraft 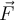 ausgeübt, während Block
ausgeübt, während Block 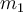 mit einem Seil an der Wand befestigt ist.
mit einem Seil an der Wand befestigt ist.Wenn der Gleitreibungskoeffizient zwischen allen Oberflächen µ ist, bestimme:
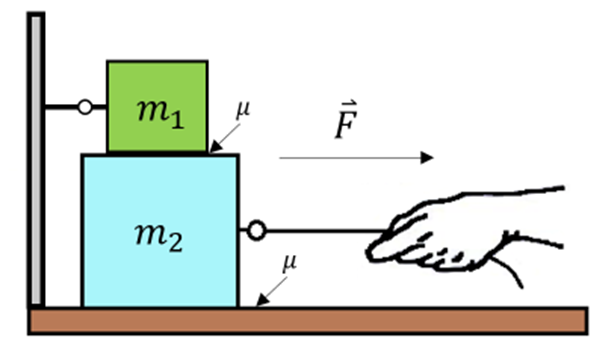
Lösung:
Betrachten wir die Freikörperbilder für jeden Block separat. Der Block
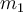 bewegt sich nicht und durch Anwendung des zweiten Newtonschen Gesetzes haben wir:
bewegt sich nicht und durch Anwendung des zweiten Newtonschen Gesetzes haben wir: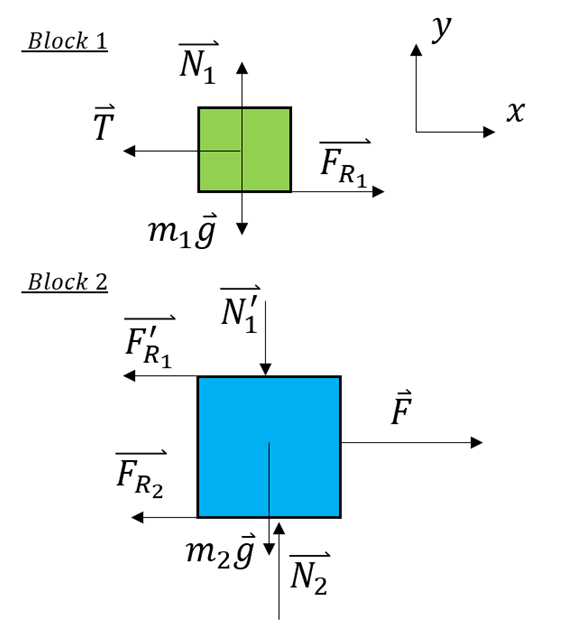
Die Kombination der Gleichungen (1) und (2) ergibt die Spannung im Seil:
Andererseits beschleunigt Block
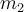 nach rechts:
nach rechts:Ersetzen der Ausdrücke von
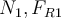 und
und 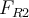 :
:Durch Multiplikation und Lösung der beiden vorherigen Gleichungen erhalten wir die Beschleunigung a von
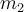 :
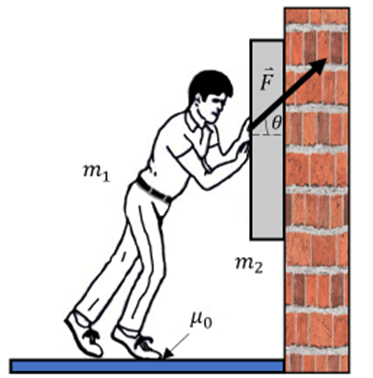
:4) Eine Person mit einem Gewicht von
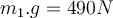 hält einen Schrank mit einem Gewicht von
hält einen Schrank mit einem Gewicht von 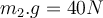 im Ruhezustand an der Wand. Die Person übt eine Kraft vom Betrag
im Ruhezustand an der Wand. Die Person übt eine Kraft vom Betrag 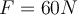 aus, die mit der Horizontalen einen Winkel
aus, die mit der Horizontalen einen Winkel 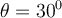 bildet. Finde:
bildet. Finde:- a) Den Mindestwert des Haftreibungskoeffizienten zwischen den Schuhen der Person und dem Boden, damit sie nicht rutschen.
- b) Den Betrag und die Richtung der von der Wand auf den Schrank ausgeübten Reibungskraft
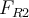 .
.
Lösung:
a) Wir machen das freie Körperdiagramm der Person im kritischen Zustand (kurz vor dem Rutschen).
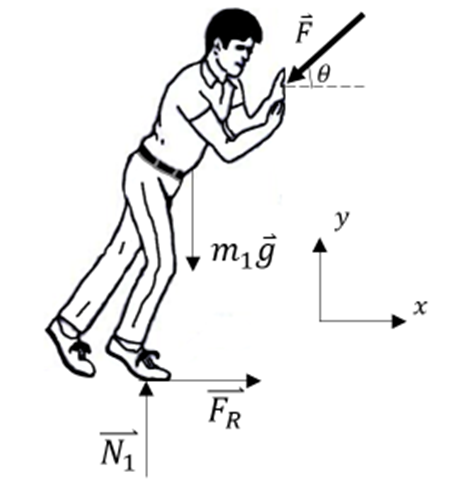
Lösen wir
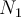 aus Gleichung (1) und setzen es in Gleichung (2) ein, erhalten wir:
aus Gleichung (1) und setzen es in Gleichung (2) ein, erhalten wir:Der Mindestwert des Haftreibungskoeffizienten beträgt:
b) Um das Gleichgewicht zu halten, ist die Summe der vertikalen Kräfte Null:
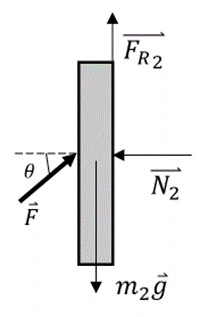
Die Reibungskraft, die ein Verrutschen des Schranks verhindert, beträgt:
5) Der „Rotor“ von Vergnügungsparks besteht aus einem rotierenden Zylinder mit einem Boden, der verschwindet, nachdem die Menschen dank Fliehkraft und Reibung an der Wand haften bleiben. Angenommen, ein Student mit einer Masse
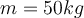 wird in eine Trommel mit einem Radius
wird in eine Trommel mit einem Radius 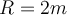 gesetzt, die eine Rotationswinkelgeschwindigkeit von
gesetzt, die eine Rotationswinkelgeschwindigkeit von 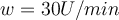 erreicht.
erreicht.- a) Wie groß ist die Normalkraft, die den Schüler gegen die Wand drückt?
- b) Wie groß muss der Haftreibungskoeffizient
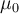 zwischen Schüler und Wand mindestens sein?
zwischen Schüler und Wand mindestens sein? - c) Angenommen, sein Freund, ein
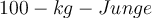 , wird jetzt in die Trommel gesetzt. Fällt dieser aus der Trommel, wenn der Boden entfernt wird?
, wird jetzt in die Trommel gesetzt. Fällt dieser aus der Trommel, wenn der Boden entfernt wird?
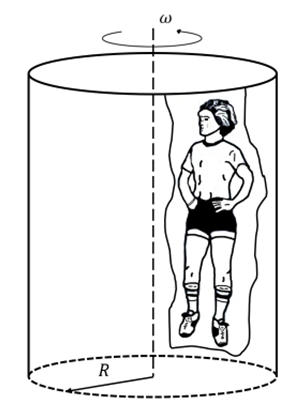
Lösung:
a) Laut einem Trägheitsbeobachter verursacht die von der Wand der Trommel auf den Student ausgeübte Normalkraft die zentripetale Beschleunigung bei seiner Bewegung:
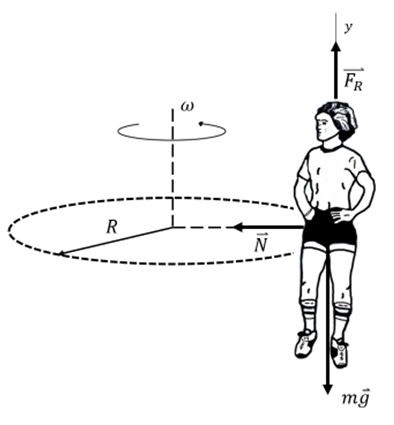
b) Die Haftreibungskraft muss das Gewicht des Studenten ausgleichen. Daher muss der Mindestwert des Haftreibungskoeffizienten eingehalten werden, damit er nicht rutscht:
Verwenden folgenden Ausdruck für die Normalkraft.
c) Der Zusammenhang zwischen
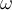 und dem Koeffizienten von
und dem Koeffizienten von 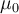 ist unabhängig von der Masse der Person. Deshalb bleibt auch der
ist unabhängig von der Masse der Person. Deshalb bleibt auch der 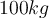 schwere junge Mann hängen, solange sein Reibungskoeffizient größer ist als der Mindestwert
schwere junge Mann hängen, solange sein Reibungskoeffizient größer ist als der Mindestwert 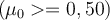 .Kleidung aus Seide verboten! ;) (Seide hat einen sehr niedrigen Reibungskoeffizienten.)
.Kleidung aus Seide verboten! ;) (Seide hat einen sehr niedrigen Reibungskoeffizienten.)

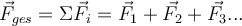
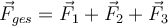
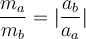
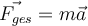
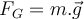
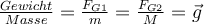
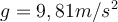
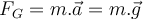
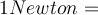
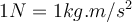
![[F]= \frac{[M][L]}{[T]^2} [F]= \frac{[M][L]}{[T]^2}](https://moodle.thga.de/filter/tex/pix.php/87eb77838a6e847b4dc625d877506c45.png)

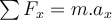
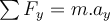
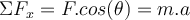
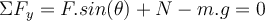
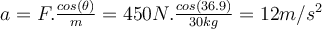
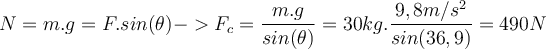
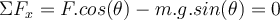
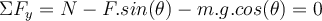
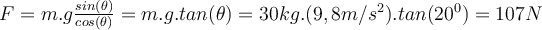
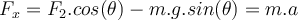
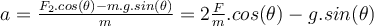
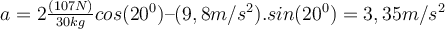
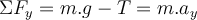
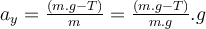
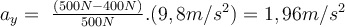
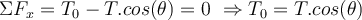
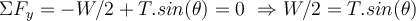
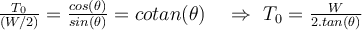
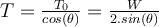
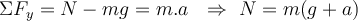
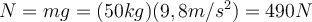
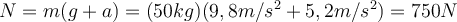
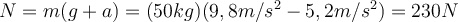
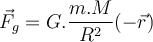
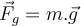
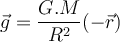
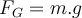
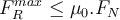

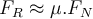
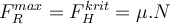
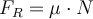
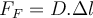
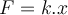
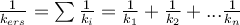
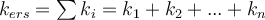
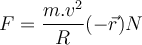
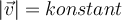
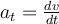
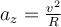
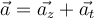
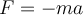
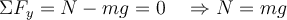
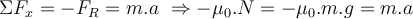
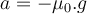
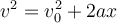
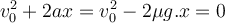
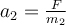

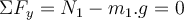
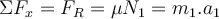
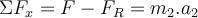
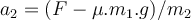
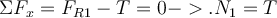
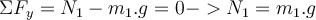
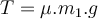
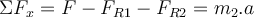
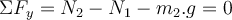
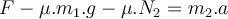
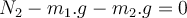
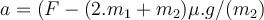
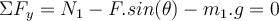
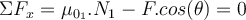
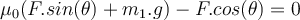
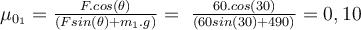
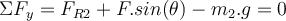
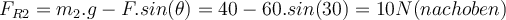
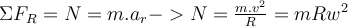
![N= (50kg) (2m)[ (30 U/min)(2 \pi rad/U)(min/s) ]^2 = 987 N N= (50kg) (2m)[ (30 U/min)(2 \pi rad/U)(min/s) ]^2 = 987 N](https://moodle.thga.de/filter/tex/pix.php/5763fb1bb1ba3e639b1170613ced5437.png)