Physik 05 - Dynamik II
Abschnittsübersicht
-
In diesem Modul lernen wir das Thema Dynamik kennen. Dynamik ist der Zweig der Mechanik. In diesem Zweig können Fragen beantwortet werden, wie zum Beispiel; Was führt dazu, dass sich ein stationäres Objekt in Bewegung setzt oder was verlangsamt oder beschleunigt ein Objekt?
In der Dynamik werden zwei grundlegende Elemente und Konzepte verwendet: Masse und Kraft! Diese sind verantwortlich für die Bestimmung der Wechselwirkungen, die zwischen dem Körper und einem anderen Körper in seiner Umgebung bestehen. Die Dynamik basiert auf den drei Gesetzen, die von Isaac Newton 1687 formuliert wurden. Diese Gesetze sind als Ergebnis der Verallgemeinerung der Erkenntnisse von Newton und anderen Wissenschaftlern, die ihm vorausgingen, insbesondere Galileo, entstanden. Die drei Newtonschen Gesetze sind ein logisches, strenges und geschlossenes System von Prinzipien, die die Säulen der klassischen oder Newtonschen Mechanik bilden.
Am Ende dieses Modul sollst du:
- die Konzepte von Arbeit und Energie kennen.
- Arbeit, die von verschiedenen Arten von Kräften geleistet wird untersuchen.
- die verschiedenen Energiearten in einem System kennen.
- Energieerhaltung verstehen.
- die konservativen und nicht-konservativen Kräfte kennen.
- Potenzialenergie- und Gleichgewichtsdiagramme verstehen.
Bevor du beginnst, noch kurz einige Infos zum Ablauf: Das Modul ist so aufgebaut, dass du mit dem Eingangstest starten solltest. Als Ergebnis bekommst eine Empfehlung, mit welchem Level der Übungen du in den jeweiligen Themen fortfahren solltest. Du kannst dieser Empfehlung folgen oder aber selber entscheiden welche Inhalte du dir ansehen und welche Übungen du machen möchtest. Zum Schluss solltest du dann den Abschlusstest absolvieren, an dessen Ende dich wiederum ein Feedback erwartet. 🙌
Die Bearbeitunsgdauer für das gesamte Modul kann bis zu 2,5 Stunden betragen. ⌛️ Wirkt das abschreckend? Dann lies besser noch etwas weiter.😉 Es ist nur eine ungefähre Einschätzung die darauf basiert, dass du dir alle Inhalte ausführlich ansiehst und jede einzelne Rechnung in allen Leveln durchführst. Du entscheidest allerdings frei in welchem Tempo du dir das Modul ansehen und welche Übungen du machen möchtest. Außerdem kannst du das Modul jederzeit verlassen und zurückkommen und dort weitermachen wo du aufgehört hast. ⏯-
Arbeit und Energie
Energie spielt eine entscheidende Rolle in unserem Leben; Es ist eines der wichtigsten Konzepte in der Physik und vielleicht das am schwierigsten zu definierende. Wir sagen, dass ein Objekt Energie besitzt, wenn es eine physikalische Veränderung an sich selbst oder seiner Umgebung hervorrufen kann. Energie nimmt viele Formen an: gravitativ, elektromagnetisch, chemisch, nuklear usw. und das Wichtigste ist, dass diese verschiedenen Formen miteinander in Beziehung stehen und von einer Form in eine andere umgewandelt werden können, so dass die Gesamtenergie immer konstant ist. Ein Konzept, das eng mit Energie verbunden ist, ist Arbeit.
Arbeit ist etwas, das an Objekten verrichtet wird, während Energie etwas ist, das Objekte besitzen. Eine Person ist in der Lage, dank der Energie, die durch die Nahrung, die sie zu sich nimmt, bereitgestellt wird, zu arbeiten. Im Kontext des Alltags sprechen wir von Arbeit mit verschiedenen Bedeutungen, und manchmal auf eine vage und ungenaue Weise. Arbeit verbinden wir meist damit, etwas zu tun oder auszuführen. "Pablo hat viel Arbeit investiert, um das Thema zu bestehen." „Lisa hat ihre Abschlussarbeit vorgestellt.“ Wir werden sehen, dass das Konzept der Arbeit in der Physik, obwohl es eine gewisse Beziehung zu unserer intuitiven Idee hat, eine sehr spezifische Bedeutung hat. Arbeit bezieht sich auf das Produkt aus einer Kraft und der Verschiebung parallel zu dieser Kraft. Wenn also keine Verschiebung auftritt, wurde keine Arbeit geleistet. Eine Energieform, die eng mit Arbeit verbunden ist, ist „kinetische Energie“. Oder Bewegung. Das Arbeits-Energie-Theorem, das wir in diesem Modul studieren werden, bezieht die Änderung der kinetischen Energie eines Objekts auf die an ihm verrichtete Arbeit. Wir werden sehen, dass dieser Satz, obwohl er eine indirekte Art der Anwendung der Newtonschen Gesetze ist, ein mächtiges Werkzeug ist, das es uns ermöglicht, viele Aspekte der Bewegung zu verstehen und Probleme zu lösen, die durch direkte Anwendung der Newtonschen Gesetze schwieriger wären.
-
Arbeit einer konstanten Kraft
Stelle dir ein Teilchen vor, das entlang einer Geraden eine Verschiebung
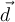 erfährt, während auf es eine Kraft
erfährt, während auf es eine Kraft 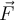 wirkt. Diese Kraft ist konstant.
wirkt. Diese Kraft ist konstant. 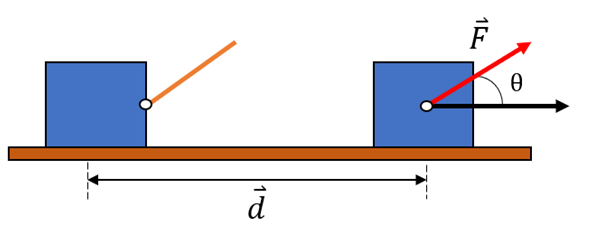
Arbeit einer Kraft .G. Jimenez
Die von der Kraft geleistete Arbeit ist definiert als das Produkt aus dem Betrag der Verschiebung
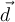 und der Komponente der Kraft parallel zur Verschiebung
und der Komponente der Kraft parallel zur Verschiebung 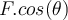
Diese Beziehung entspricht dem Skalarprodukt:
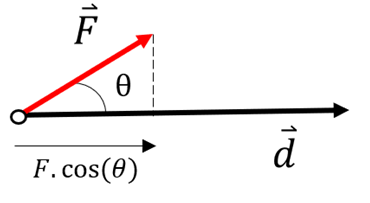
Arbeit einer Kraft (Zerlegung der Kraft). G. Jimenez Nach dieser Definition wirkt eine Kraft nur dann auf ein Objekt, wenn:
- Wenn sich das Objekt bewegt
- Die Kraft eine Komponente in Verschiebungsrichtung hat.
Drei Fälle können auftreten:
- Wenn
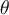 zwischen 0° und 90° liegt:
zwischen 0° und 90° liegt: 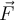 hat eine Komponente in gleicher Richtung und gleichem Verschiebungssinn und die Arbeit ist positiv
hat eine Komponente in gleicher Richtung und gleichem Verschiebungssinn und die Arbeit ist positiv - Wenn
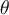 gleich 90° ist:
gleich 90° ist: 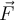 steht senkrecht auf der Verschiebung und die Arbeit ist Null.
steht senkrecht auf der Verschiebung und die Arbeit ist Null. - Wenn
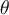 zwischen 90° und 180° liegt:
zwischen 90° und 180° liegt:  hat eine zur Verschiebung entgegengesetzte Komponente und die Arbeit ist negativ.
hat eine zur Verschiebung entgegengesetzte Komponente und die Arbeit ist negativ.
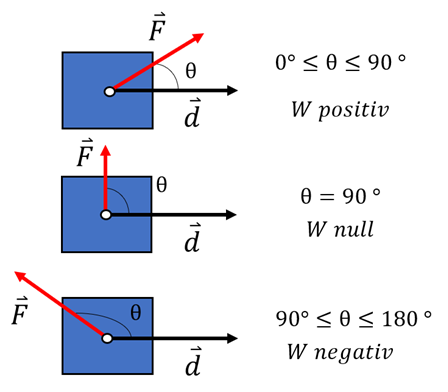
Arbeit einer konstanten Kraft. G. Jimenez Nehme den Fall eines Gewichthebers, er arbeitet, während er die Gewichte vom Boden hebt, aber sobald er sie in Ruhe auf eine bestimmte Höhe hält, arbeitet er während dieser Zeit nicht mehr an den Gewichten.
Aus physiologischer Sicht verrichtet der Mensch mikroskopische Arbeit. Seine Muskeln kontrahieren und entspannen sich immer wieder, der Mann schwitzt und atmet schwer, er wird müde und erschöpft und Sie müssen ihm Energie (Nahrung) zuführen, damit es so bleibt.
Selbst wenn die Person mit den Gewichten in einer bestimmten Höhe und konstanter Geschwindigkeit horizontal geht, verrichtet sie keine Arbeit an den Gewichten, da die Kraft, die sie ausübt, um sie zu halten, vertikal nach oben gerichtet ist, während die Verschiebung horizontal ist.
Arbeit einer vertikalen Kraft. .G. Jimenez Internationale Systemeinheit für Arbeit:
-
Arbeit mit variabler Kraft
Stelle dich nun in einem Körper vor, der sich entlang einer gekrümmten Bahn von
 nach
nach 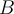 bewegt. Bei einer infinitesimalen Verschiebung ist die von der variablen Kraft
bewegt. Bei einer infinitesimalen Verschiebung ist die von der variablen Kraft 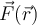 verrichtete Arbeit das Skalarprodukt:
verrichtete Arbeit das Skalarprodukt:Die Gesamtarbeit von A nach B ist die Summe der Arbeit, die bei den aufeinanderfolgenden Verschiebungen geleistet wird, und ist das Linienintegral entlang des Bewegungspfads.
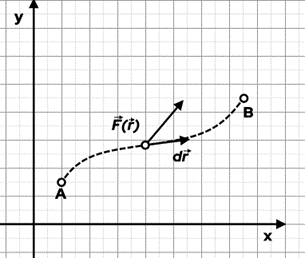
Arbeit einer veränderlichlen Kraft. N. Donner Arbeit als Fläche unter der Kurve.
Wenn sich der Körper bewegt, ändert sich die tangentiale Komponente der Kraft
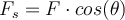 . Wenn wir
. Wenn wir 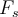 als Funktion der entlang des Pfades gemessenen Entfernung
als Funktion der entlang des Pfades gemessenen Entfernung 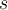 auftragen, sehen wir, dass die infinitesimale Arbeit
auftragen, sehen wir, dass die infinitesimale Arbeit  der Fläche des gezeigten elementaren Rechtecks entspricht in der Figur.
der Fläche des gezeigten elementaren Rechtecks entspricht in der Figur.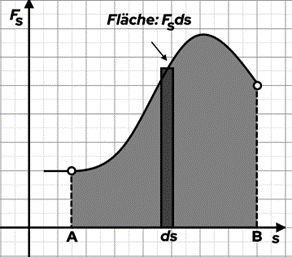
Arbeit als Fläche unter der Kurve. N. Donner Daher ergibt sich die Gesamtarbeit aus der Summe der Flächen der Rechtecke, entspricht also der schraffierten Fläche.
Arbeit, um eine Feder zu dehnen
Die von einer Feder ausgeübte Kraft ist eine Rückstellkraft, d.h. sie hat die entgegengesetzte Richtung zur Verschiebung.
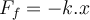 . Wenn ein externes Mittel versucht, eine Feder zu dehnen, muss es eine Kraft aufbringen, die gleich groß und der Federkraft entgegengesetzt ist.
. Wenn ein externes Mittel versucht, eine Feder zu dehnen, muss es eine Kraft aufbringen, die gleich groß und der Federkraft entgegengesetzt ist.Wenn sich die Verschiebung aus dem Gleichgewicht von
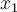 nach
nach 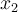 ändert, beträgt die vom externen Agenten geleistete Arbeit:
ändert, beträgt die vom externen Agenten geleistete Arbeit:Die Arbeit der auf die Feder ausgeübten Kraft ist positiv, wenn
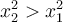 , das heißt, wenn die Größe der Endverschiebung größer ist als die der Anfangsverschiebung (dies tritt auf, wenn die Feder gedehnt oder zusammengedrückt wird).
, das heißt, wenn die Größe der Endverschiebung größer ist als die der Anfangsverschiebung (dies tritt auf, wenn die Feder gedehnt oder zusammengedrückt wird).Die von der Feder geleistete Arbeit ist das Negativ der vom externen Agenten geleisteten Arbeit
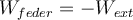
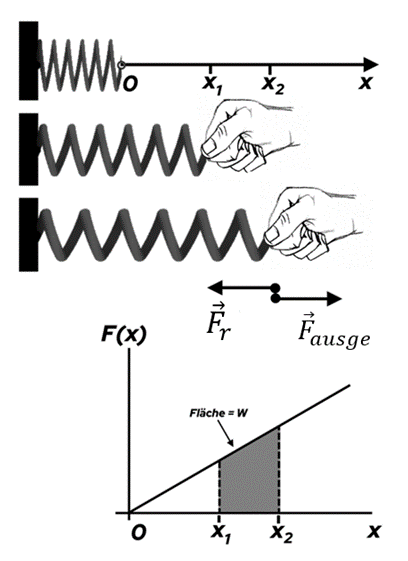
Arbeit einer Feder. N. Donner Arbeit-Energie Theorem
Betrachte die elementare Arbeit, die eine Kraft auf ein Teilchen der Masse
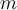 verrichtet, das eine infinitesimale Verschiebung
verrichtet, das eine infinitesimale Verschiebung 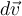 hat. Nach dem zweiten Newtonschen Gesetz gilt:
hat. Nach dem zweiten Newtonschen Gesetz gilt:Wenn wir berücksichtigen, dass
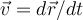 und dass das Skalarprodukt kommutativ ist.
und dass das Skalarprodukt kommutativ ist.Wir haben:
Um die Gesamtarbeit auf dem Weg von A nach B zu finden, integrieren wir diese Gleichung:
Die Größe
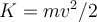 heißt kinetische Energie des Masseteilchens
heißt kinetische Energie des Masseteilchens 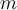 , das eine Geschwindigkeit
, das eine Geschwindigkeit 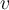 hat. Das obige Ergebnis ist als Arbeits-Energie-Theorem bekannt.
hat. Das obige Ergebnis ist als Arbeits-Energie-Theorem bekannt."Die Arbeit, die die Nettokraft auf ein Teilchen verrichtet, ist gleich der Änderung seiner kinetischen Energie."
Der Arbeits- und Energiesatz besagt, dass sich die kinetische Energie eines Körpers nur ändert, wenn eine äußere Kraft auf ihn einwirkt:
- Ist die Arbeit negativ (die Nettokraft wirkt der Bewegung entgegen), nimmt die kinetische Energie ab.
Wenn wir zum Beispiel einen Ball in die Luft werfen, verrichtet die Schwerkraft (das Gewicht
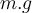 ) beim Aufsteigen negative Arbeit und seine kinetische Energie nimmt ab
) beim Aufsteigen negative Arbeit und seine kinetische Energie nimmt ab  , bis er sofort stoppt, wenn er das Höhenmaximum erreicht .
, bis er sofort stoppt, wenn er das Höhenmaximum erreicht .- Wenn die Arbeit positiv ist. (die Nettokraft wirkt in die gleiche Bewegungsrichtung), die kinetische Energie nimmt zu.
Wenn zum Beispiel eine Kugel unter der Wirkung der Schwerkraft fällt, verrichtet ihr Gewicht m.g positive Arbeit und ihre kinetische Energie nimmt zu
 .
.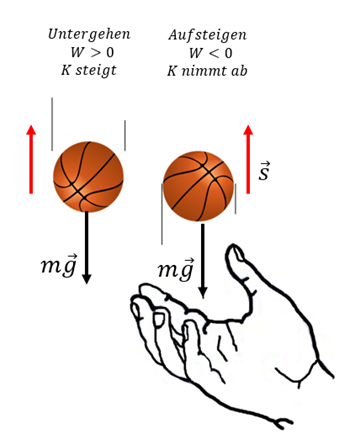
Arbeit-Energie Theorem. G. Jimenez Das Work-Energy Theorem besagt, dass bei verrichteter Arbeit eine Veränderung oder Übertragung von Energie stattfindet. Allgemein lässt sich sagen, dass Arbeit ein Maß für die Energieübertragung ist.
Leistung
In der Praxis ist es wichtig, nicht nur die an einem Objekt verrichtete Arbeit zu kennen, sondern auch die Kraft oder Geschwindigkeit, mit der diese Arbeit verrichtet wird:
Die von der Kraft
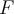 bei einer infinitesimalen Verschiebung dr verrichtete Arbeit ist
bei einer infinitesimalen Verschiebung dr verrichtete Arbeit ist 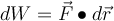 und als Geschwindigkeit
und als Geschwindigkeit 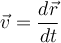 ist die Momentanleistung:
ist die Momentanleistung:Das Skalarprodukt der auf ein Objekt wirkenden Kraft multipliziert mit der Geschwindigkeit des Objekts ist die Leistung, die von dem Agenten geliefert wird, der die Kraft ausübt.
IS-Einheit der Leistung
Die IS-Einheit der Leistung entspricht der Arbeit oder Energie pro Zeiteinheit, also
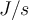
Diese Einheit heißt Watt (Symbol
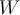 ) und entspricht einem Joule an Energie, die in einer Sekunde übertragen wird.
) und entspricht einem Joule an Energie, die in einer Sekunde übertragen wird. -
Beispiele: Arbeit und Energie
1) Ein Mann zieht ein Schwein der Masse
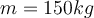 mit einer konstanten Kraft
mit einer konstanten Kraft 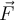 von
von 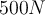 in einem Winkel von
in einem Winkel von 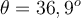 zur Horizontalen über eine horizontale Fläche. Nehmen Sie an, dass sich das Schwein starr bewegt, wobei der Gleitreibungskoeffizient
zur Horizontalen über eine horizontale Fläche. Nehmen Sie an, dass sich das Schwein starr bewegt, wobei der Gleitreibungskoeffizient 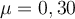 ist.
ist.Wenn das Schwein über eine horizontale Entfernung von
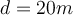 gezogen wurde, bestimme:
gezogen wurde, bestimme:- a) Die Arbeit, die durch die vom Mann aufgebrachte Kraft verrichtet wird
- b) Die von der Reibungskraft verrichtete Arbeit
- c) Die durch die Schwerkraft verrichtete Arbeit
- d) Die von der Normalkraft verrichtete Arbeit
- e) Was ist die Netzarbeit am Schwein?
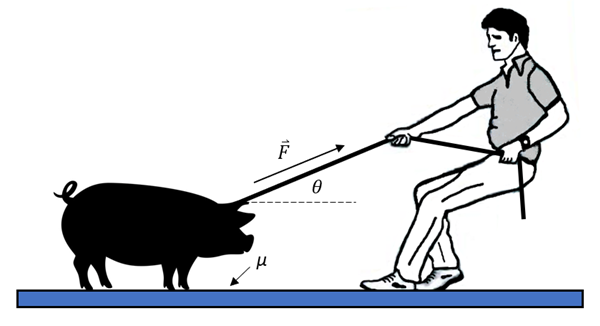
Lösung:
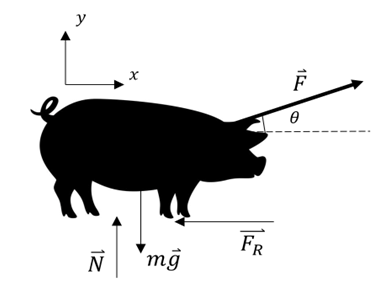
a) Die Arbeit der vom Mann aufgebrachten Kraft
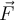 ist:
ist:b) Die Summe aller Vertikalkräfte ist Null:
Gleitreibungskraft:
Sie hat die entgegengesetzte Richtung zur Verschiebung, daher ist die von dieser Kraft geleistete Arbeit negativ:
c) Das Gewicht mg steht senkrecht auf der Verschiebung d und seine Arbeit ist Null:
d) Aus dem gleichen Grund ist die Arbeit der Normalkraft
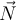 gleich Null:
gleich Null:e) Die am Schwein geleistete Gesamtarbeit ist die Summe:
2) Ein Mann der Masse m, der sich an einem Seil festhält, lässt sich von einem Helikopter auf das Dach eines Gebäudes herab. Der Mann startet aus der Ruhe und steigt mit einer konstanten Beschleunigung der Größe
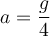 eine Höhe
eine Höhe 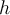 hinab.
hinab.- a) Finden Sie die Arbeit, die der Hubschrauber an dem Mann geleistet hat.
- b) Finden Sie die Arbeit, die der Mann durch die Schwerkraft verrichtet.
- c) Wie groß ist die kinetische Endenergie des Menschen?
- d) Wie groß ist die Endgeschwindigkeit des Mannes?
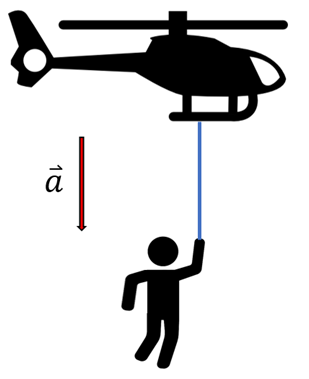
Lösung:
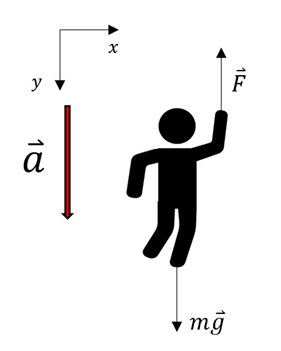
a) Um die Kraft F zu finden, die der Hubschrauber auf den Mann ausübt, wenden wir das zweite Newtonsche Gesetz an:
Da die Kraft der Verschiebung entgegengerichtet ist, ist die von F verrichtete Arbeit negativ:
b) Die Gewichtskraft mg hat die gleiche Richtung wie die Verschiebung und die Arbeit ist positiv:
c) Die am Menschen geleistete Netzwerkarbeit ist die Summe:
Wir wenden den Arbeits- und Energiesatz an:
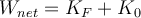 Da der Mensch aus der Ruhe startet, ist seine endgültige kinetische Energie:
Da der Mensch aus der Ruhe startet, ist seine endgültige kinetische Energie:d) Die Endgeschwindigkeit des Mannes ergibt sich aus der Bewegungsenergie:
3) Ein Mann transportiert eine Last mit einem reibungsfreien Karren über eine horizontale Fläche. Wenden Sie auf dem Weg von
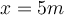 nach
nach 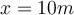 eine zunehmende Kraft an:
eine zunehmende Kraft an:Bildet einen Winkel θ mit der Horizontalen ebenfalls zunehmend, gemäß der Beziehung
Wobei
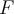 in Newton und
in Newton und 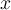 in Metern gemessen wird. Welche Arbeit leistet der Mensch auf dieser Reise?
in Metern gemessen wird. Welche Arbeit leistet der Mensch auf dieser Reise? 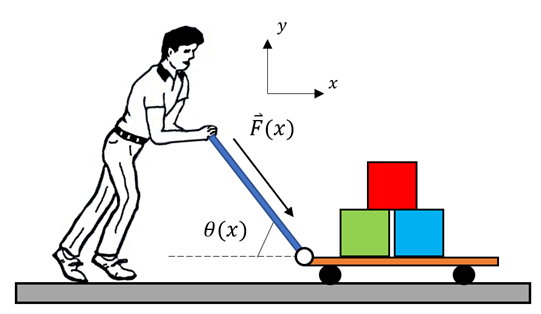
Lösung:
a) Für eine elementare Verschiebung dx ist die von der Kraft verrichtete Arbeit:
Wenn wir diesen Ausdruck zwischen den Grenzen
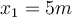 und
und 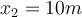 integrieren, haben wir:
integrieren, haben wir:Deswegen
4) Ein Block der Masse
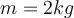 wird langsam mit einem Winkel
wird langsam mit einem Winkel 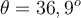 und
und 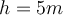 einen Hang hinaufbewegt. Der Gleitreibungskoeffizient zwischen Objekt und Oberfläche steigt linear von einem Wert
einen Hang hinaufbewegt. Der Gleitreibungskoeffizient zwischen Objekt und Oberfläche steigt linear von einem Wert 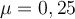 auf einen Wert
auf einen Wert 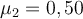 an. Erledigte Arbeit finden.
an. Erledigte Arbeit finden.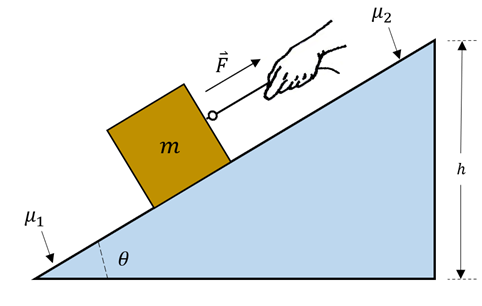
Lösung:
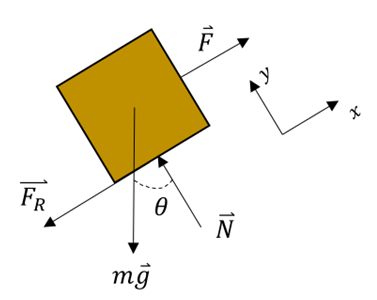
Da der Block mit konstanter Geschwindigkeit steigt, lauten die Gleichgewichtsgleichungen:
Wenn wir diese Gleichungen kombinieren, finden wir die aufgebrachte Kraft:
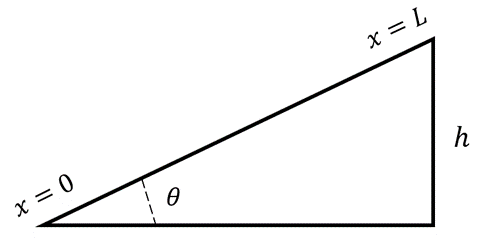
Der Gleitreibungskoeffizient wird durch den Ausdruck angegeben:
Mit diesem Ausdruck berechnen wir die geleistete Arbeit:
-
Energieerhaltung
Die Energieerhaltung ist ein grundlegendes Prinzip von entscheidender Bedeutung in der Physik und von grundlegender Bedeutung in der Natur. Innerhalb eines Systems können wir zwei Arten von Kräften unterscheiden: konservative und nicht-konservative. Eine Kraft wird als konservativ bezeichnet, wenn ihre Arbeit nur von der Anfangs- und Endposition des Objekts abhängt und nicht vom zurückgelegten Weg. Wir haben bereits zwei Beispiele konservativer Kräfte gesehen: die Schwerkraft und die elastische Kraft einer Feder. Es gibt auch Kräfte oder Konservative wie Reibung, deren Arbeit von dem Weg abhängt, dem das Objekt folgt. Konservative Kräfte zeichnen sich durch die Möglichkeit der Energiespeicherung aus der Konfiguration der Systemteile aus. Die so gespeicherte Energie wird potentielle Energie genannt. In jedem isolierten System von Objekten, die durch konservative Kräfte interagieren, kann Energie von kinetischer in potentielle und umgekehrt umgewandelt werden, aber die Summe dieser (mechanische Energie) bleibt konstant. In einer realen Situation wird es immer nicht-konservative oder dissipative Kräfte wie Reibung geben. Die Arbeit der Reibungskräfte verringert die mechanische Energie und wird vom Auftreten thermischer Energie begleitet, die auf mikroskopischer Ebene nichts anderes ist als die kinetische Energie von Atomen und Molekülen in zufälliger Bewegung und sich in einem Temperaturanstieg manifestiert. Unter Berücksichtigung aller möglichen Energieformen ändert sich die Gesamtenergie eines Systems plus der seiner Umgebung nicht, obwohl Reibung vorhanden ist. Dies stellt das Prinzip der Energieerhaltung dar.
Konservative Kräfte:
Wir können zwei Arten von Kräften unterscheiden: konservative und nicht-konservative. Eine Kraft ist konservativ, wenn die Arbeit, die sie an einem Objekt verrichtet, das sich von einer beliebigen Anfangsposition A zu einer beliebigen Endposition B bewegt, nur von diesen beiden Positionen abhängt und nicht von dem speziellen Weg, dem das Objekt folgt.
Wenn wir die beiden beliebigen Pfade von Punkt A nach Punkt B betrachten, ist die von einer konservativen Kraft verrichtete Arbeit gleich, unabhängig davon, ob das Objekt Pfad
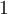 oder Pfad
oder Pfad 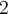 folgt.
folgt.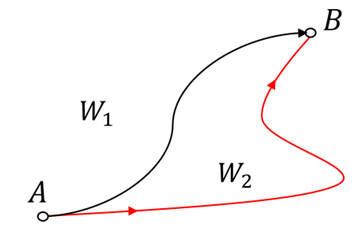
Konservative Kräfte. G. Jimenez Eine äquivalente Definition lautet: Eine Kraft ist konservativ, wenn das Netzwerk, das sie bewirkt, für ein Objekt, das sich auf einem beliebigen geschlossenen Weg bewegt, Null ist.
Angenommen, das Objekt geht von
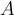 nach
nach 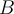 entlang Weg 1, die verrichtete Arbeit ist
entlang Weg 1, die verrichtete Arbeit ist 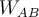 . Wenn wir auf dem gleichen Weg von B nach A zurückkehren, ist die Kraft an jedem Punkt gleich, aber die Verschiebung
. Wenn wir auf dem gleichen Weg von B nach A zurückkehren, ist die Kraft an jedem Punkt gleich, aber die Verschiebung 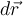 ist in die
entgegengesetzte Richtung, daher der entsprechende Beitrag
ist in die
entgegengesetzte Richtung, daher der entsprechende Beitrag 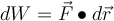 hat das entgegengesetzte Vorzeichen wie vorher und als Ergebnis bei der Berechnung der Gesamtarbeit:
hat das entgegengesetzte Vorzeichen wie vorher und als Ergebnis bei der Berechnung der Gesamtarbeit: 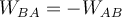 Da die Arbeit tut nicht
vom Weg abhängen, wenn man von B nach A auf einem anderen Weg wie 2 zurückkehrt, lohnt sich die Arbeit immer noch
Da die Arbeit tut nicht
vom Weg abhängen, wenn man von B nach A auf einem anderen Weg wie 2 zurückkehrt, lohnt sich die Arbeit immer noch 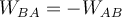 . Daher ist die Netzwerkarbeit, die geleistet wird, um von A nach B und wieder zurück nach A zu gelangen:
. Daher ist die Netzwerkarbeit, die geleistet wird, um von A nach B und wieder zurück nach A zu gelangen: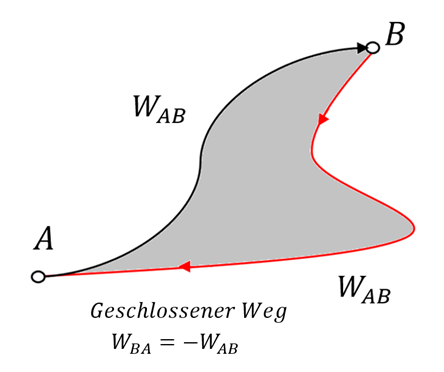
Konservative Kraft (geschlossener Weg) .G. Jimenez Die Schwerkraft ist eine konservative Kraft. Wir haben im vorigen Kapitel an mehreren Beispielen gesehen, dass die von der Schwerkraft geleistete Arbeit nicht vom zurückgelegten Weg abhängt, sondern nur von der Differenz zwischen der Endhöhe und der Anfangshöhe. Betrachten wir einen hochgeschleuderten Block auf einer „glatten“ schiefen Ebene der Höhe h, so ist die durch die Schwerkraft auf den Block verrichtete Arbeit auf dem Weg nach oben
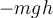 und auf dem Rückweg
und auf dem Rückweg 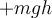 . Daher ist die auf dem
Hin- und Rückweg geleistete Netzarbeit gleich Null:
. Daher ist die auf dem
Hin- und Rückweg geleistete Netzarbeit gleich Null: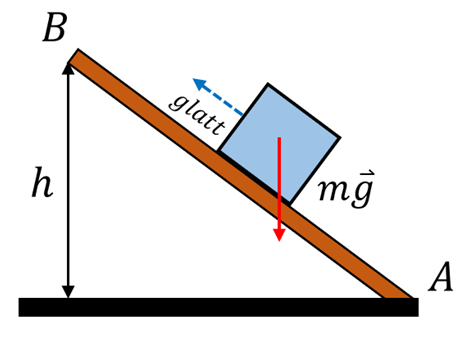
Konservative Schwerkraft. G. Jimenez Nichtkonservative Kräfte:
Reibung ist die häufigste nicht-konservative Kraft, der wir bei mechanischen Problemen begegnen. In dem obigen Beispiel, in dem der Block die sanfte Steigung hinaufgeschleudert wird, ist die einzige Kraft, die auf den Block in Verschiebungsrichtung wirkt, die Komponente der Schwerkraft, und der Block kehrt mit der gleichen kinetischen Energie wie ursprünglich zum Ausgangspunkt zurück. das heißt, die kinetische Energie bleibt erhalten.
Nehmen wir nun an, dass die schiefe Ebene rauh ist. Wenn der Block nach oben geschleudert wird, wirkt die kinetische Reibungskraft
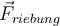 der Verschiebung
der Verschiebung 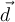 entgegen. Die Arbeit dieser Kraft wird sowohl auf dem Weg nach oben
(
entgegen. Die Arbeit dieser Kraft wird sowohl auf dem Weg nach oben
( 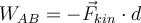 ) als auch auf dem Weg nach unten (
) als auch auf dem Weg nach unten (  ). Es ist keine Stornierung möglich, und das Netz auf der gesamten Hin- und Rückfahrt,
). Es ist keine Stornierung möglich, und das Netz auf der gesamten Hin- und Rückfahrt, 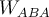 , ist ungleich Null. Daher ist die kinetische
Reibungskraft nicht konservativ. Wenn der Block in seine ursprüngliche Position zurückkehrt, gewinnt er nicht die kinetische Energie zurück, die er am Anfang hatte.
, ist ungleich Null. Daher ist die kinetische
Reibungskraft nicht konservativ. Wenn der Block in seine ursprüngliche Position zurückkehrt, gewinnt er nicht die kinetische Energie zurück, die er am Anfang hatte.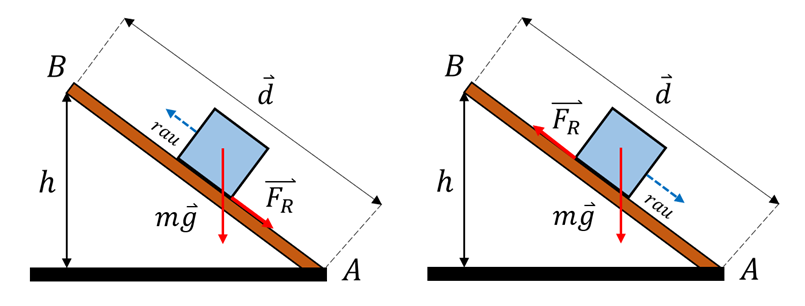
Nichtkonservative Kraft. G. Jimenez Potenzielle Energie
Eine konservative Kraft kann einer skalaren Funktion zugeordnet werden, die potentielle Energie genannt wird. Wenn eine konservative Kraft auf ein Objekt wirkt, das sich zwischen den Punkten A und B bewegt, definieren wir die Änderung der potentiellen Energie als den negativen Wert der von dieser Kraft geleisteten Arbeit.
Potenzielle Energie ist die aufgrund der relativen Position von zwei oder mehr interagierenden Körpern gespeicherte Energie.
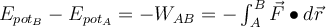
Die Änderung der potentiellen Energie ist das Negative der von der konservativen Kraft verrichteten Arbeit.Potentielle Energie der Gravitation
In der Nähe der Erdoberfläche ist die Schwerkraft konstant und zeigt senkrecht nach unten. Die Änderung der potentiellen Energie eines Objekts ist das Negative der von der Gravitationskraft geleisteten Arbeit.
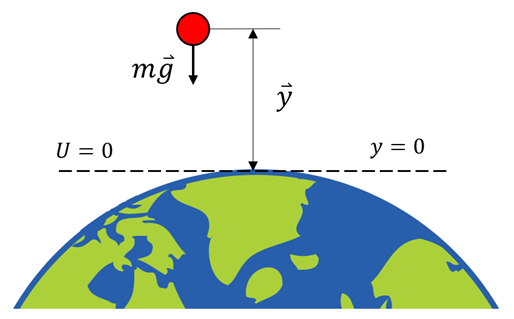
Pottentialle Energie der Gravitation. G. Jimenez Wählt man den Ursprung
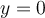 an der Erdoberfläche mit
an der Erdoberfläche mit 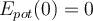 , so ist die Gravitationspotentialenergie in Höhe
, so ist die Gravitationspotentialenergie in Höhe 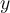
Elastische potentielle Energie:
Potenzielle Energie kann auch in einem Objekt wie einer Feder aufgrund ihrer Verformung gespeichert werden. Die von einer Feder ausgeübte Kraft ist der Dehnung
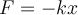 entgegengerichtet. Die Änderung der potentiellen Energie des Objekts beim Bewegen
von Null nach
entgegengerichtet. Die Änderung der potentiellen Energie des Objekts beim Bewegen
von Null nach 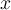 ist das Negative der Arbeit, die die Feder auf das Objekt verrichtet, wenn es sich von
ist das Negative der Arbeit, die die Feder auf das Objekt verrichtet, wenn es sich von 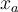 nach
nach 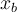 bewegt:
bewegt:Wenn wir als Referenz am Ursprung
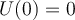 nehmen, haben wir:
nehmen, haben wir: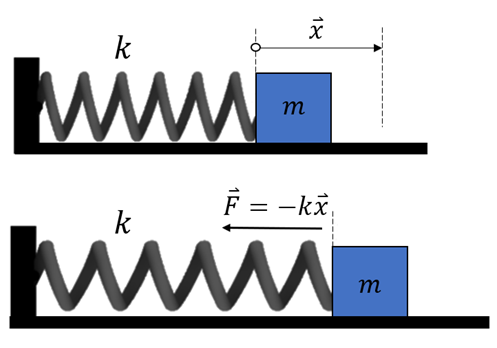
Elastische potentielle Energie. G. Jimenez Mechanische Energie und ihre Erhaltung:
Angenommen, die einzigen Kräfte, die auf einen Körper wirken, sind konservativ. Kombiniert man den Arbeits- und Energiesatz (
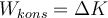 ) mit der Definition der potentiellen Energie (
) mit der Definition der potentiellen Energie ( 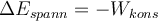 ), erhält man:
), erhält man:Deswegen:
Dies ist das Prinzip der Erhaltung der mechanischen Energie: Wenn auf ein System nur konservative Kräfte einwirken, bleibt die gesamte mechanische Energie (kinetische plus potentielle) konstant.
Prinzip der Erhaltung der mechanischen Energie: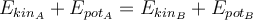
Die gesamte mechanische Energie eines isolierten Systems bleibt in Abwesenheit nichtkonservativer Kräfte konstant.Arbeit nichtkonservativer Kräfte:
Die Änderung der kinetischen Energie eines Objekts hängt von allen Kräften ab, sowohl von konservativen als auch von nicht-konservativen. Nach dem Arbeits-Energie-Theorem haben wir:
Nun ändert die Arbeit der konservativen Kräfte die potentielle Energie des Systems:
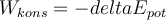 . Daher können wir schreiben:
. Daher können wir schreiben:Das heißt, die von den nichtkonservativen Kräften verrichtete Arbeit ist gleich der Abnahme der mechanischen Energie.
In einem isolierten System ist die Arbeit der nichtkonservativen Kräfte gleich der Änderung der gesamten mechanischen Energie des Systems.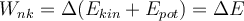
Wärmeenergie:
Wenn ein Objekt über eine raue Oberfläche gleitet, wirkt die Reibungskraft der Bewegung entgegen und reduziert so seine kinetische Energie. Die durch das Objekt verlorene kinetische Energie wird in innere Energie der zufälligen Bewegungen der Atome und Moleküle umgewandelt, aus denen es besteht. Diese übertragene Energie wird als Endenergie bezeichnet und äußert sich in einer Erhöhung der Temperatur des Blocks. Nach einer Weile kühlt der Block ab. Die dabei gewonnene Wärmeenergie wird als Wärme an seine Umgebung abgegeben, wobei der Energieübertragungsmechanismus ausschließlich mit der Temperaturdifferenz zwischen dem heißen Block und der kühleren Umgebung zusammenhängt.
Eine Eigenschaft der thermischen Energie ist, dass ihre Erzeugung nicht reversibel ist. Mit anderen Worten, die Atome können nicht in ihren ursprünglichen Zustand zurückkehren und die als makroskopische kinetische Energie des Blocks erworbene Energie abgeben. Im Gegensatz dazu wird die Energie, die zum Zusammendrücken einer Feder aufgewendet wird, vollständig zurückgewonnen, nachdem die Feder wieder gedehnt wurde.
Thermische Energie eines Körpers: Die zufällige kinetische Energie seiner Atome und Moleküle.Reibung erzeugt thermische Energie, die das System nicht zurückgewinnt. -
Prinzip der Energieerhaltung
Die von einer konservativen Kraft geleistete Arbeit ist rückgewinnbar, da sie die Energie zwischen kinetischer und potentieller Energie so austauscht, dass ihre Summe (gesamte mechanische Energie) immer konstant bleibt.
Wenn die Kraft nicht konservativ ist, geht ein Teil der geleisteten Arbeit nicht in den mechanischen Energieaustausch, sondern geht durch Reibung oder eine andere Ursache verloren. Wenn das System isoliert ist, manifestiert sich die verlorene Energie als kinetische Energie der Atome und Moleküle, aus denen das System besteht (thermische Energie), und aufgrund der relativen Positionen der Atome darin auch als potentielle Energie (elektrischer Natur). das System, die Moleküle. Die Energie der Atome und Moleküle, aus denen das System besteht, ist die innere Energie.
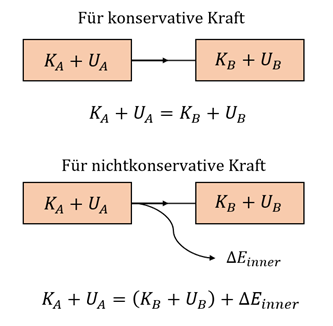
Prinzip der Energieerhaltung. G. Jimenez Es ist eine experimentelle Tatsache, dass in einem isolierten System, wenn alle möglichen Energieformen berücksichtigt werden, die Energie von einer Form in eine andere umgewandelt werden kann, aber die Gesamtenergie konstant bleibt:
Das ist das Prinzip der Energieerhaltung.
Energieeehaltung: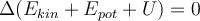
In einem isolierten System kann Energie von einer Art in eine andere umgewandelt, aber nicht zerstört werden.Kraft: abgeleitet von potentieller Energie
Nach der Definition der potentiellen Energie ist eine infinitesimale Änderung der potentiellen Energie dU das Negative der Elementararbeit, die eine konservative Kraft F bei einer infinitesimalen Verschiebung
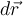 verrichtet:
verrichtet:Wenn wir die potentielle Energie als Funktion einer einzigen Koordinate
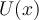 betrachten, können wir schreiben:
betrachten, können wir schreiben:Das heißt, die Arbeit einer konservativen Kraft kann immer durch eine potentielle Energiefunktion dargestellt werden. Nicht so für eine nicht-konservative Kraft:
Diagramme von Energie und Gleichgewicht
Um ein konservatives System qualitativ zu analysieren, ist es sehr nützlich, einen Graphen von U gegen x zu erstellen. Wenn U(x) die Gravitationspotentialenergie ist, könnte die Form der Kurve mit dem Profil einer gekrümmten Bahn übereinstimmen, auf der eine Kugel rollt.
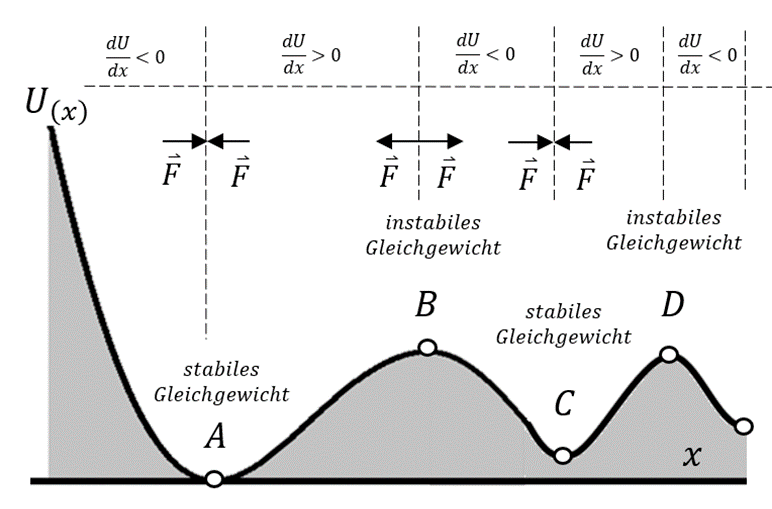
Diagramme von Energie und Gleichgewicht. G.Jimenez Da
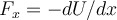 , sind die Gleichgewichtspunkte diejenigen, bei denen die Steigung Null ist. Der Charakter des Gleichgewichts könnte sein: stabil, instabil oder neutral (indifferent):
, sind die Gleichgewichtspunkte diejenigen, bei denen die Steigung Null ist. Der Charakter des Gleichgewichts könnte sein: stabil, instabil oder neutral (indifferent):- An Punkten wie A und C, für die U(x) minimal ist, ist das Gleichgewicht stabil, da, wenn sich das Teilchen leicht zu einer Seite bewegt, die Kraft auf die gegenüberliegende Seite gerichtet ist und dazu neigt, es in seine Gleichgewichtsposition zurückzubringen.
- An einem Punkt wie B, für den U(x) maximal ist, ist das Gleichgewicht instabil, da, wenn sich das Teilchen leicht zu einer Seite bewegen würde, die Kraft dazu neigt, es weiter vom Gleichgewichtspunkt wegzudrücken.
- In Bereichen, in denen U konstant ist (Punkt D), besteht ein neutrales Gleichgewicht, da die kleinen Verschiebungen des Teilchens in Bezug auf diese Positionen keine Rückstellkraft erzeugen.
Problemlösungsstrategie
Die Energieerhaltung ist ein allgemeiner physikalischer Grundsatz, der für mechanische Systeme den Newtonschen Gesetzen entspricht. Es ist ein leistungsstarkes alternatives Werkzeug zum Lösen von Problemen, die ansonsten sehr schwierig sein könnten. Um es anzuwenden, wird empfohlen, die folgende Strategie zu befolgen.
- Identifizieren Sie die Körper, die das System bilden
- Identifizieren Sie alle wirkenden Kräfte
- Bestimmen Sie, welche Kräfte konservativ sind und welche nicht.
- Finden Sie die potenziellen Energien, die mit den konservativen Kräften verbunden sind.
- Bei nur konservativ wirkenden Kräften bleibt die mechanische Energie erhalten. Setzen Sie die mechanische Energie zu einem bestimmten Zeitpunkt mit der zu einem anderen Zeitpunkt gleich.
- Bei nichtkonservativen Kräften ist die mechanische Energie nicht konstant. Setzen Sie die Arbeit der nichtkonservativen Kräfte mit der Differenz zwischen der mechanischen Endenergie und der mechanischen Anfangsenergie gleich.
-
Beispiele: Energieerhaltung
1) Ein Körper der Masse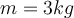 wird aus einer Höhe
wird aus einer Höhe 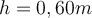 auf eine Plattform fallen gelassen, die von einer Feder mit der elastischen Konstante
auf eine Plattform fallen gelassen, die von einer Feder mit der elastischen Konstante 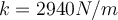 getragen wird. Bestimmen Sie den maximalen Weg, um den die Feder zusammengedrückt wird.
getragen wird. Bestimmen Sie den maximalen Weg, um den die Feder zusammengedrückt wird.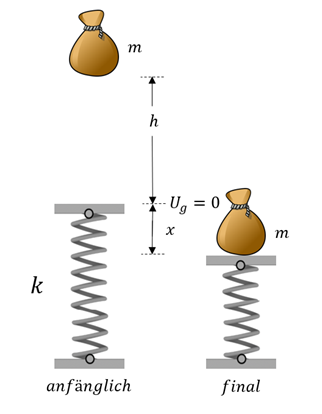
Lösung:
Da alle Kräfte konservativ sind, bleibt die gesamte mechanische Energie erhalten. In beiden Situationen, Anfangs- und Endsituation, ist die Geschwindigkeit null und damit auch die kinetischen Energien
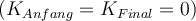 . Nimmt man als Nullniveau der potenziellen Gravitationsenergie
. Nimmt man als Nullniveau der potenziellen Gravitationsenergie 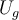 in der Anfangsposition
in der Anfangsposition 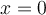 des freien Endes der Feder, wir schreiben:
des freien Endes der Feder, wir schreiben:Durch Umstellen erhält man die quadratische Gleichung in x:
Wessen Wurzeln sind:
Durch Einsetzen der Zahlenkonstanten erhält man die Lösung
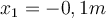 und
und 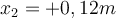 . Die negative Wurzel wird verworfen, da sie eine Dehnung der Feder darstellen würde, was nicht der Fall ist. Daher beträgt die maximale Kompression der Feder:
. Die negative Wurzel wird verworfen, da sie eine Dehnung der Feder darstellen würde, was nicht der Fall ist. Daher beträgt die maximale Kompression der Feder:2) Ein Block startet aus einer Höhe von
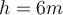 und rutscht eine gekrümmte reibungsfreie Bahn hinunter. Der Block gleitet dann eine grobe Steigung hinauf, die mit der Horizontalen einen Winkel
und rutscht eine gekrümmte reibungsfreie Bahn hinunter. Der Block gleitet dann eine grobe Steigung hinauf, die mit der Horizontalen einen Winkel 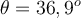 bildet. Wenn die maximal erreichte Höhe
bildet. Wenn die maximal erreichte Höhe 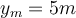 beträgt, bestimmen Sie den Gleitreibungskoeffizienten zwischen dem Klotz und der schiefen Ebene.
beträgt, bestimmen Sie den Gleitreibungskoeffizienten zwischen dem Klotz und der schiefen Ebene.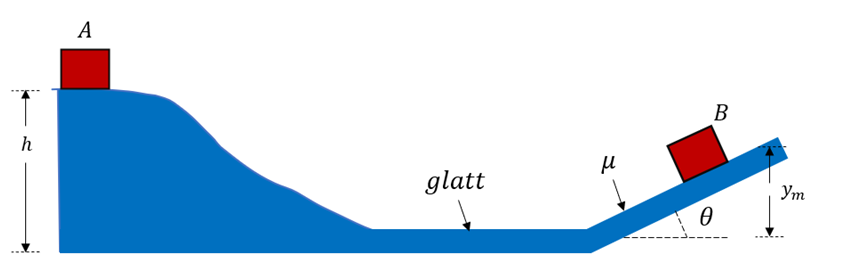
Lösung:
Die Änderung der gesamten mechanischen Energie (kinetisch + potentiell) zwischen der Endposition und der Ausgangsposition ist die Arbeit der nichtkonservativen Reibungskraft:
Mit
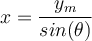 ist die Verschiebung in der schiefen Ebene:
ist die Verschiebung in der schiefen Ebene:Beim Lösen finden wir den Gleitreibungskoeffizienten:
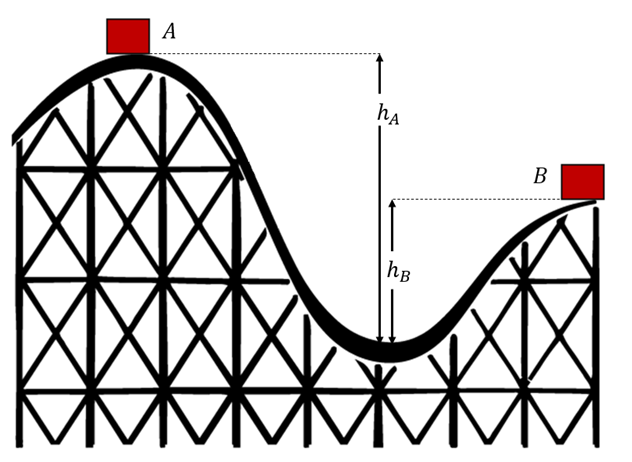
3) Auf einer Achterbahn startet ein Karren von der Ruheposition am Punkt
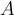 und rollt die reibungsfreie Bahn hinunter. Wenn
und rollt die reibungsfreie Bahn hinunter. Wenn 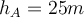 und
und 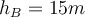 , was ist der minimale Sicherheitsradius des Wagens für die Krümmung der Strecke an Punkt
, was ist der minimale Sicherheitsradius des Wagens für die Krümmung der Strecke an Punkt 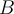 ?
?
Lösung:
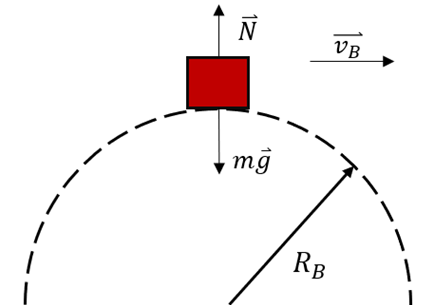
Anwendung der Energieerhaltung zwischen den Positionen
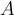 und
und 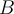 des Wagens:
des Wagens: 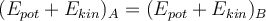
Unter Berücksichtigung von
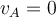 erhalten wir:
erhalten wir:Anwenden des zweiten Newtonschen Gesetzes in radialer Richtung auf den Wagen an Position B:
Der Höchstwert der zulässigen Geschwindigkeit bei Kontaktverlust mit der Landebahn
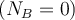 entspricht der Bedingung:
entspricht der Bedingung:4) In einer Zirkusshow radelt ein Radfahrer auf einer vertikalen kreisförmigen Bahn bis zur Position
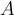 und fährt danach ohne Treten bergauf. Wenn der Radius des Kreises
und fährt danach ohne Treten bergauf. Wenn der Radius des Kreises 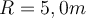 beträgt und der Schwerpunkt der Person mit ihrem Fahrrad in einer Höhe
beträgt und der Schwerpunkt der Person mit ihrem Fahrrad in einer Höhe 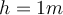 über dem Boden liegt, mit welcher Mindestgeschwindigkeit muss sie den Punkt
über dem Boden liegt, mit welcher Mindestgeschwindigkeit muss sie den Punkt 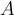 erreichen, um die vollständige zu erreichen Runde, ohne den Kontakt zur Strecke zu verlieren.
erreichen, um die vollständige zu erreichen Runde, ohne den Kontakt zur Strecke zu verlieren.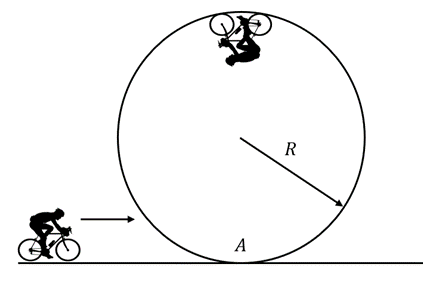
Lösung:
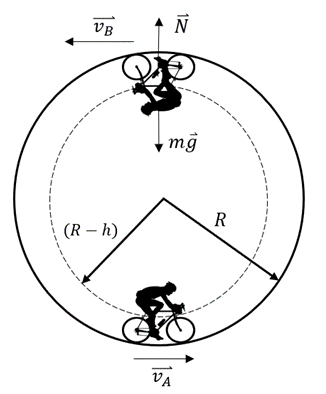
Wenden wir die Energieerhaltung an, wenn der Radfahrer von Position
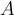 (null potentielle Energie) nach oben bei
(null potentielle Energie) nach oben bei 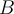 fährt, erhalten wir:
fährt, erhalten wir:Wenden wir das zweite Newtonsche Gesetz in radialer Richtung am Punkt
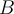 an, können wir schreiben:
an, können wir schreiben:Die kritische Geschwindigkeit
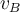 muss gerade so groß sein, dass am Punkt
muss gerade so groß sein, dass am Punkt 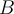 die Normalkraft
die Normalkraft 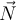 Null ist:
Null ist:Durch Einsetzen der Beziehung
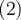 in
in 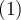 erhalten wir:
erhalten wir:Daher muss die Mindestgeschwindigkeit bei
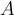 sein:
sein:

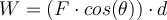
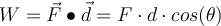
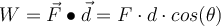
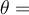
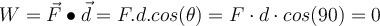
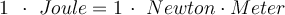
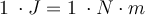
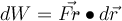
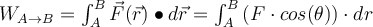
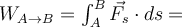
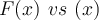
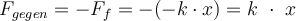
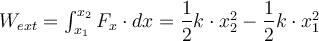
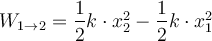
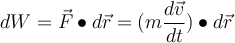
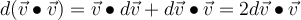
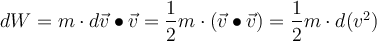
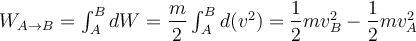
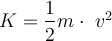
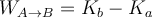
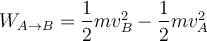
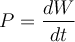
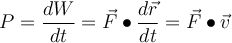
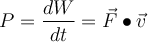
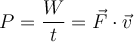
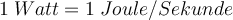
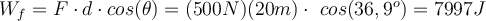
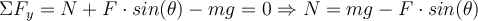
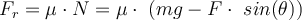
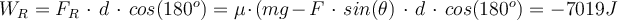
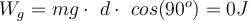
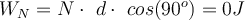
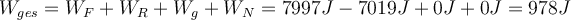
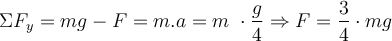
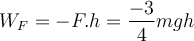
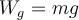
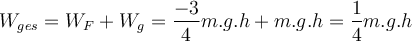
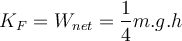
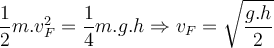
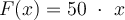
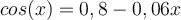
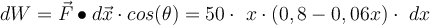
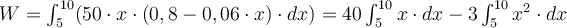
![W= 40 \cdot (x^2/2)^{10}_5-3[x^3/3]^{10}_5=625J W= 40 \cdot (x^2/2)^{10}_5-3[x^3/3]^{10}_5=625J](https://moodle.thga.de/filter/tex/pix.php/772015b0e451aad0240e03756861a619.png)
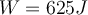
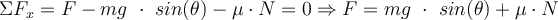
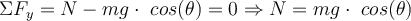
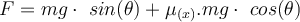
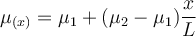
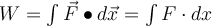
![W= \int ^{L}_{0} [ mg\cdot sin( \theta )+( \mu_1+(\mu_2-\mu_1) \dfrac{x}{L}) \cdot mg\cdot cos(\theta)] \cdot dx W= \int ^{L}_{0} [ mg\cdot sin( \theta )+( \mu_1+(\mu_2-\mu_1) \dfrac{x}{L}) \cdot mg\cdot cos(\theta)] \cdot dx](https://moodle.thga.de/filter/tex/pix.php/508e22590b2a960b1c8b07b7807a9b1b.png)
![W= [mg\cdot (sin(\theta)+\mu_1.cos(\theta))\cdot x +mg\cdot (\mu_2-\mu_1)\cdot cos(\theta) \dfrac{x^2}{2L}]^L_0 W= [mg\cdot (sin(\theta)+\mu_1.cos(\theta))\cdot x +mg\cdot (\mu_2-\mu_1)\cdot cos(\theta) \dfrac{x^2}{2L}]^L_0](https://moodle.thga.de/filter/tex/pix.php/2fe151ccbe7e958c66281d2345d97976.png)
![W=mg\cdot L\cdot [(sin(\theta)+\mu_1\cdot cos(\theta)) +\dfrac{1}{2}(\mu_2-\mu_1)\cdot cos(\theta)] W=mg\cdot L\cdot [(sin(\theta)+\mu_1\cdot cos(\theta)) +\dfrac{1}{2}(\mu_2-\mu_1)\cdot cos(\theta)]](https://moodle.thga.de/filter/tex/pix.php/f5378fbd76e0f4990c02ed4b4a5ea9e0.png)
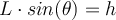
![W=mgh\cdot [1+\dfrac{\mu_2+\mu_1}{2\cdot ctg(\theta)}]=147J W=mgh\cdot [1+\dfrac{\mu_2+\mu_1}{2\cdot ctg(\theta)}]=147J](https://moodle.thga.de/filter/tex/pix.php/006d9accdd6be585d9af003fc8e04dcb.png)
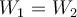
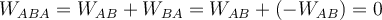
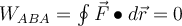
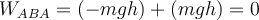
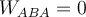
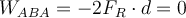
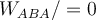
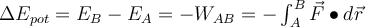
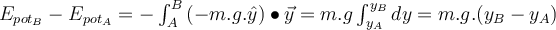
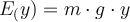
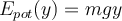
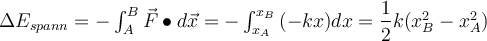
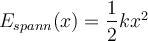
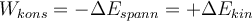
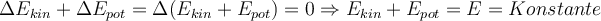
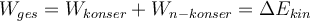
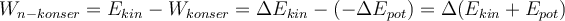
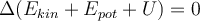
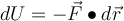
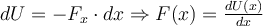
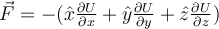
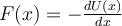
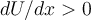
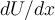
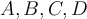
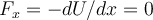
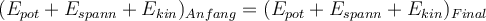
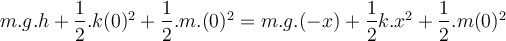
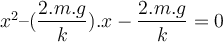
![x= \dfrac{m.g}{k} (1 \pm \sqrt[2]{ (1+\dfrac{2kh}{mg} )} ) x= \dfrac{m.g}{k} (1 \pm \sqrt[2]{ (1+\dfrac{2kh}{mg} )} )](https://moodle.thga.de/filter/tex/pix.php/136b3ebc2d5c000a12f3c5164482410f.png)
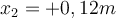
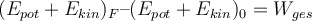
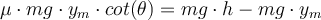
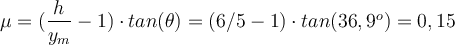
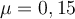
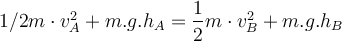
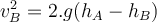
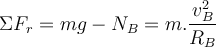
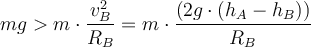
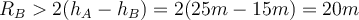
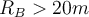
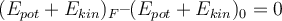
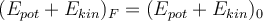
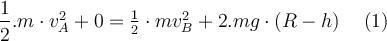
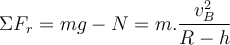
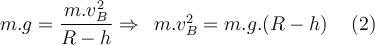
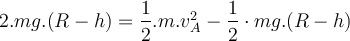
![v_A= \sqrt[2]{ 5.g\cdot (R-h)} = \sqrt[2] {(5\cdot (9,8)\cdot (5-1)}= 14\hspace {1mm}m/s v_A= \sqrt[2]{ 5.g\cdot (R-h)} = \sqrt[2] {(5\cdot (9,8)\cdot (5-1)}= 14\hspace {1mm}m/s](https://moodle.thga.de/filter/tex/pix.php/5de9ee1a5f54b0bdffeb1715f720ef8b.png)