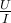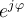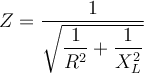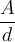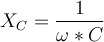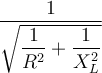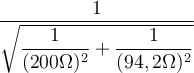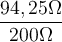Elektrotechnik 03 - Wechselstromtechnik
Abschnittsübersicht
-
In diesem Modul geht es um die Wechselstromtechnik. Unser gesamtes Stromnetz vom Erzeuger bis zum Verbraucher arbeitet mit Wechselstrom, daher ist sie ein wichtiger Teil der Elektrotechnik. Die Anwendung und die Berechnung von Wechselstrom(-schaltungen) unterscheidet sich in einigen Punkten deutlich von Gleichstrom(-schaltungen). Trotzdem empfehle ich dir, zuvor das Modul „Grundlagen der Elektrotechnik“ durchzuarbeiten. Das Kennen dieser Inhalte, insbesondere das ohmsche Gesetz und der Abschnitt „Wechselstrom/-spannung“, wird hier vorausgesetzt.
Am Ende dieses Moduls sollst du:
- Die Begriffe der Wechselstromtechnik kennen
- Einfache Berechnungen mit Spulen und Kondensatoren durchführen können
- Die Zusammenhänge zwischen verschiedenen Leistungsarten verstehen
- Die verschiedenen Leistungsarten berechnen können
-
Die Spule
Spulen, auch Induktivitäten genannt, bestehen meist aus aufgewickeltem isoliertem Kupferdraht, je nach Ausführung mit oder ohne Eisen-/Ferritkern.

Verschiedene Arten von Spulen
Electronic component inductors von FDominec ist als GFDL
gekennzeichnetFließt ein Strom durch sie hindurch wird ein Magnetfeld aufgebaut. Man kann eine Spule aber auch durch ein Magnetfeld hindurchbewegen und dadurch einen Stromfluss erzeugen.Anwendung finden sie in beispielsweise in Elektromotoren, Generatoren, Transformatoren oder auch als Energiespeicher in Netzteilen.
Die charakteristische Größe einer Spule ist ihre Induktivität. Sie trägt den Formelbuchstaben L und die Einheit H (für Henry). Üblicherweise haben Spulen eine Induktivität im Bereich von mH.
Anders als bei einem ohmschen Widerstand, haben wir an der Spule eine Phasenverschiebung zwischen Strom und Spannung. Das bedeutet, dass die charakteristischen Punkte der Sinusschwingung, wie die Nulldurchgänge, Minima und Maxima, bei Strom und Spannung nicht an der selben Stelle liegen. Das sieht dann so aus:
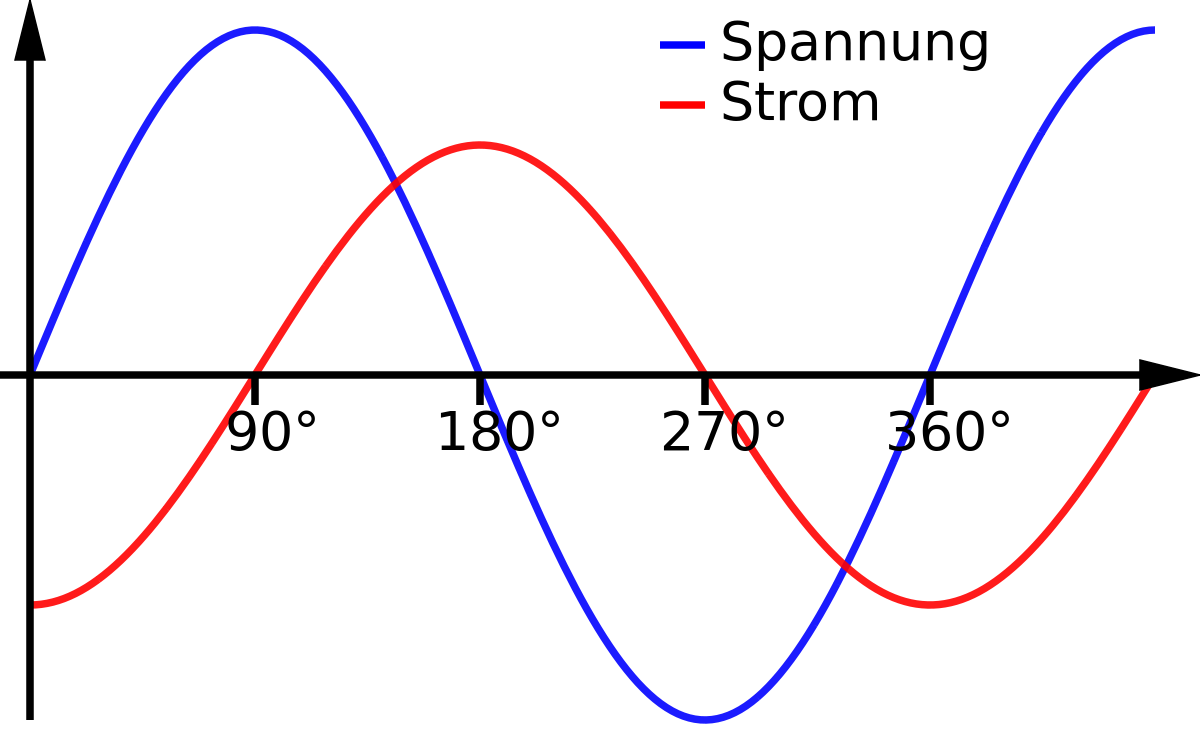
Phasenverschiebung induktiv von Hyperstryke ist als gemeinfrei gekennzeichnet Bei einer idealen Spule eilt der Strom der Spannung immer um 90° nach. Merke: „Bei Induktivitäten, die Ströme sich verspäten“
Achtung, jetzt kommen komplexe Zahlen ins Spiel. Da in der Elektrotechnik der Buchstabe i schon durch den Strom belegt ist, verwendet man hier für die komplexen Zahlen den Buchstaben j.
Der Wechselstromwiderstand wird allgemein durch:
Bei einer idealen Spule ohne ohmschen Anteil bedeutet das: R = 0 und
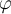 = 90°.Ideale Spulen oder Kondensatoren gibt es in der Realität nicht. Sie eignen sich für Erklärungen oder Berechnungen jedoch viel besser als reale Bauteile.Übrig bleibt also nur das X, bei einer Spule entsprechend XL. XL ist also der Wechselstromwiderstand, auch Impedanz genannt, der Spule. Die Impedanz ist abhängig von der Induktivität L und auch von der Frequenz f der anliegenden Spannung.
= 90°.Ideale Spulen oder Kondensatoren gibt es in der Realität nicht. Sie eignen sich für Erklärungen oder Berechnungen jedoch viel besser als reale Bauteile.Übrig bleibt also nur das X, bei einer Spule entsprechend XL. XL ist also der Wechselstromwiderstand, auch Impedanz genannt, der Spule. Die Impedanz ist abhängig von der Induktivität L und auch von der Frequenz f der anliegenden Spannung.Für die Spule gilt: XL =
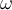 * L, wobei
* L, wobei 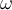 für die Kreisfrequenz steht die sich mit 2*
für die Kreisfrequenz steht die sich mit 2*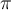 *f berechnen lässt.
*f berechnen lässt. Die Impedanz wird somit umso größer je höher die Frequenz wird. Legt man eine Spannung mit einer sehr hohen Frequenz an die Spule, wird (fast) kein Strom durch sie hindurchfließen.
Im Umkehrschluss bedeutet das, dass ein reiner Gleichstrom (f=0) die Spule ungehindert passieren kann. Durch den Stromfluss baut sich ein Magnetfeld auf. Wird die Versorgungsspannung nun abgeschaltet, wird durch die im Magnetfeld gespeicherte Energie eine Spannung mit umgekehrter Polarität erzeugt.
Reihen- Parallelschaltung von Spulen
Werden mehrere Spulen miteinander verschaltet, verhält es sich wie mit den Widerständen.
Reihenschaltung: Die Induktivitäten L und die Impedanzen XL werden einfach addiert.
L ges = L1 + L2 + L3Parallelschaltung: Die Kehrwerte der Induktivitäten und Impedanzen werden addiert.
L ges =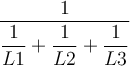 Betrachtet man eine nicht reale Spule (der Widerstand der Spulenwicklung wird hierbei berücksichtigt) oder schaltet man eine ideale Spule und einen Widerstand zusammen, so ergibt sich der folgende Zusammenhang:
Betrachtet man eine nicht reale Spule (der Widerstand der Spulenwicklung wird hierbei berücksichtigt) oder schaltet man eine ideale Spule und einen Widerstand zusammen, so ergibt sich der folgende Zusammenhang: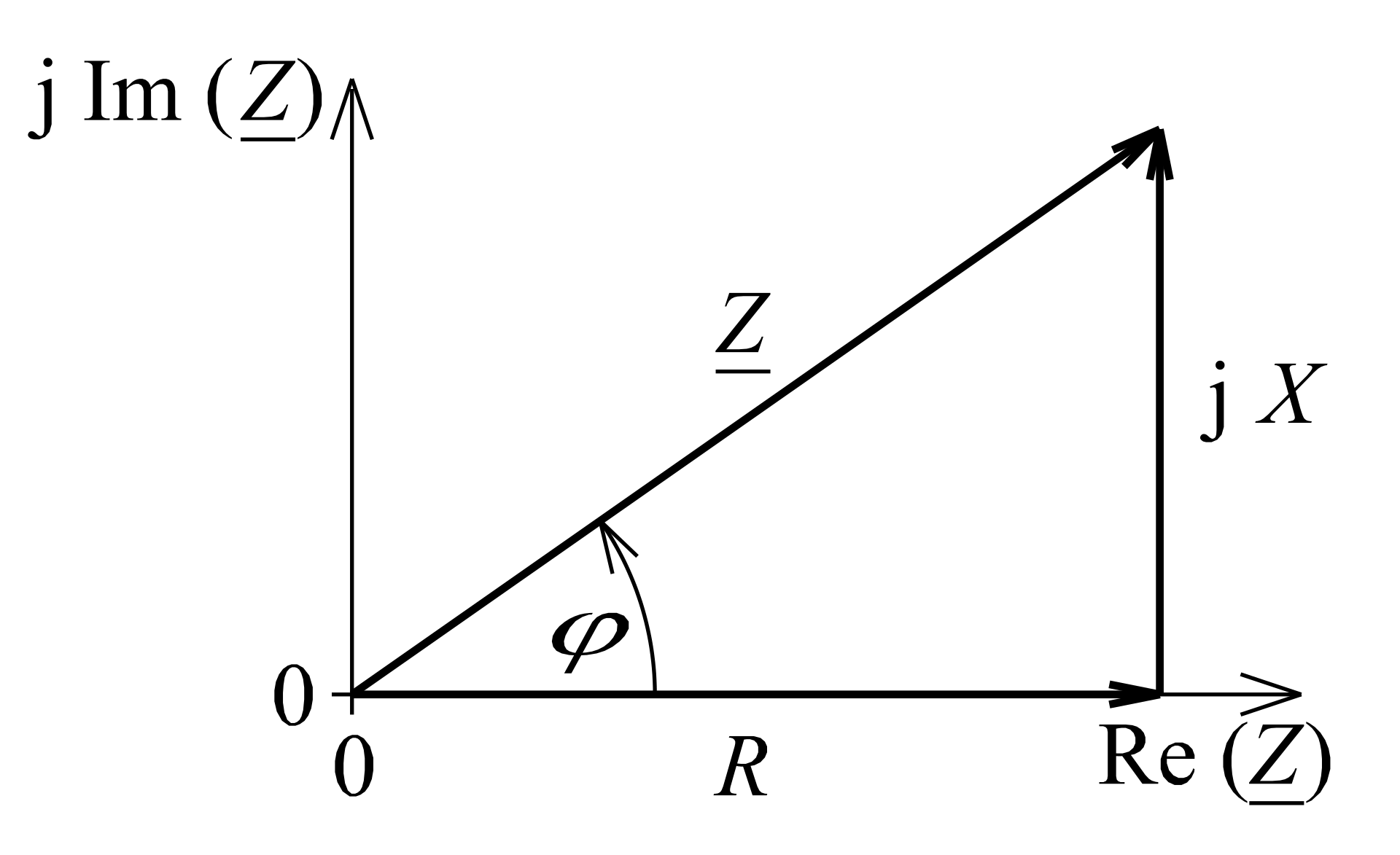
Widerstand_Zeiger von Saure ist als CC BY-SA 3.0 gekennzeichnet Für eine Reihenschaltung aus Widerstand und Spule bedeutet das, dass für die Bestimmung des Gesamtwiderstandes nicht einfach R + XL gerechnet werden kann, sondern gilt Gesamtwiderstand/-impedanz Z2 = R2 + XL2. -
Der Kondensator
Kondensatoren, auch Kapazitäten genannt, zählen ebenso wie die Spulen zu den Energiespeichern. Sie speichern Energie in Form eines elektrischen Feldes in einem Dielektrikum welches sich zwischen zwei Elektroden befindet.
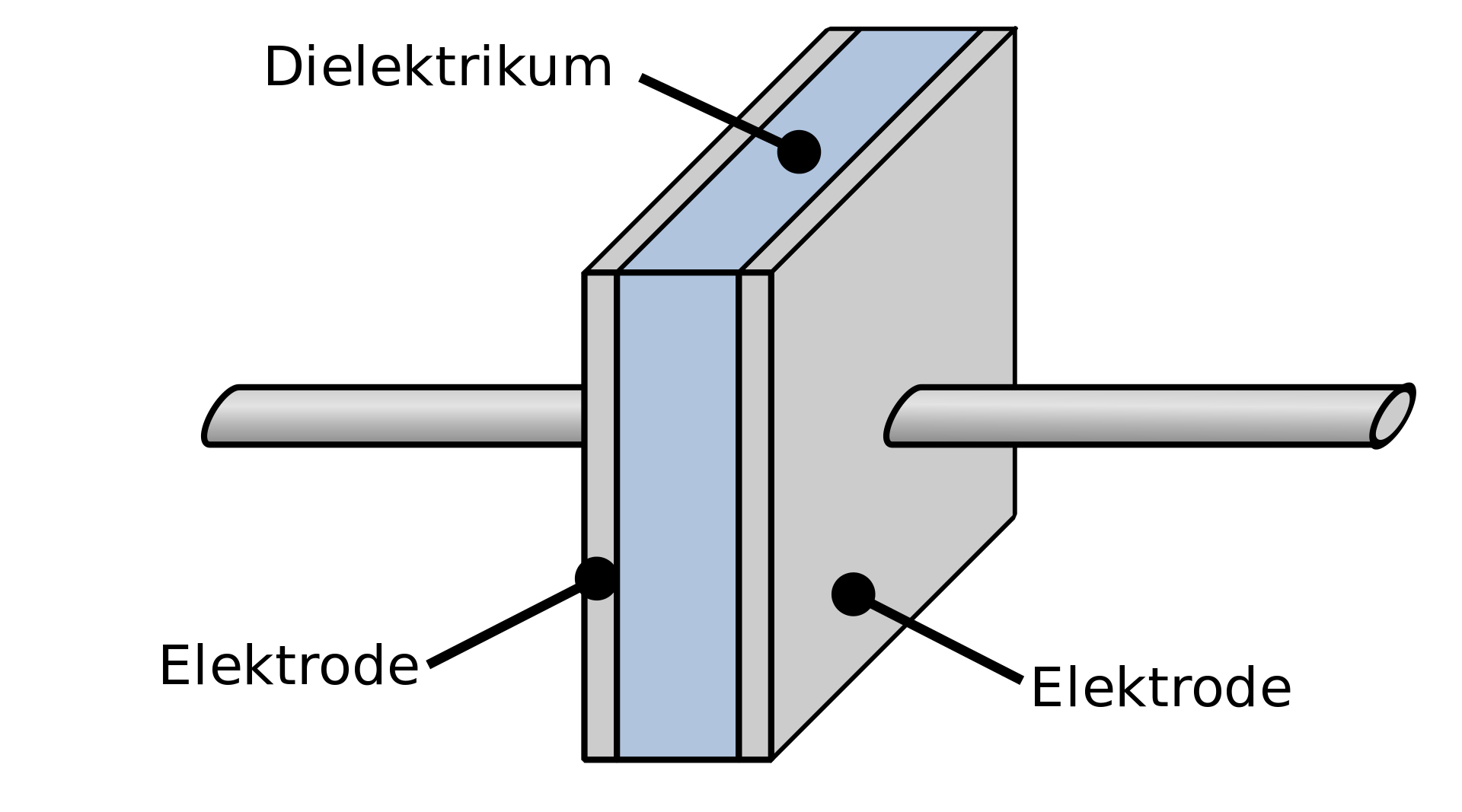
Plate_Capacitor_DE von Cepheiden ist als CC BY-SA 3.0 gekennzeichnet Kondensatoren finden z.B. dort Anwendung, wo Spannungen gepuffert oder geglättet werden sollen.
Die charakteristische Größe eines Kondensators ist seine Kapazität. Der Formelbuchstabe ist das C und die Einheit Farad, kurz F. Ein Kondensator mit einer Kapazität von einem Farad ist sehr groß und kommt nur in speziellen Anwendungen zum Einsatz. Für die meisten Anwendungen reichen Kondensatoren in den Größenordnungen von Picofarad (kurz pF, p = *10-12), Nanofarad (kurz nF, n = *10-9) oder Mikrofarad (kurz µF, µ = *10-6) völlig aus.
Ähnlich wie bei der Spule, gibt es auch am Kondensator eine Phasenverschiebung zwischen Strom und Spannung. Hier sind es allerdings nicht +90° wie an der Spule, sondern -90°. Beim Kondensator eilt also der Strom der Spannung voraus.
Die Kapazität C ist abhängig von der Fläche A und dem Abstad d der Elektroden und von der Dielektrizitätskonstanten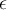 . Die Dielektrizitätskonstanten
. Die Dielektrizitätskonstanten 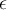 setzt sich zusammen aus der Dielektrizitätskonstanten des Vakuums
setzt sich zusammen aus der Dielektrizitätskonstanten des Vakuums 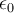 (8,85*10-12) und der Dielektrizitätskonstanten des verwendeten Dielektikums
(8,85*10-12) und der Dielektrizitätskonstanten des verwendeten Dielektikums 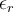 .
.Im Gegensatz zur Spule, sinkt der Wechselstromwiderstand eines Kondensators also mit steigender Frequenz.
Die Gesetzmäßigkeiten beim Verschalten mehrerer Kondensatoren unterscheidet sich ebenfalls denen von Spulen und Widerständen. Beim Parallelschalten von Kondensatoren werden die Einzelkapazitäten einfach addiert. Bei der Reihenschaltung gilt hingegen: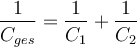
-
Leistungsarten und deren Berechnung
In dem Kurs „Grundlagen der Elektrotechnik“ hast du die Leistung schon kennengelernt. Dort ging es aber nur um ohmsche Widerstände. Die Leistung (P = U*I) die an einem ohmschen Widerstand abfällt wird komplett in Wärme umgewandelt, unabhängig davon, ob der Widerstand von einem Gleich- oder Wechselstrom durchflossen wird. Man spricht dabei von der Wirkleistung. Bei Spulen und Kondensatoren im Wechselstromkreis wird die Leistung allerdings in magnetische bzw. elektrische Felder gewandelt.
Daraus ergeben sich drei Arten von Leistungen.
1. Die Wirkleistung P [W]: Meist in Form von Wärme an einem ohmschen Verbraucher oder aber in Form von Bewegung bei einem Elektromotor.
2. Die Blindleistung Q [var]: Leistung, die benötigt wird und elektrische und magnetische Felder auf- und abzubauen.
3. Die Scheinleistung S [VA]: Die „Gesamtleistung“, setzt sich aus der Wirk- und Blindleistung zusammen, wobei gilt: S =
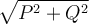
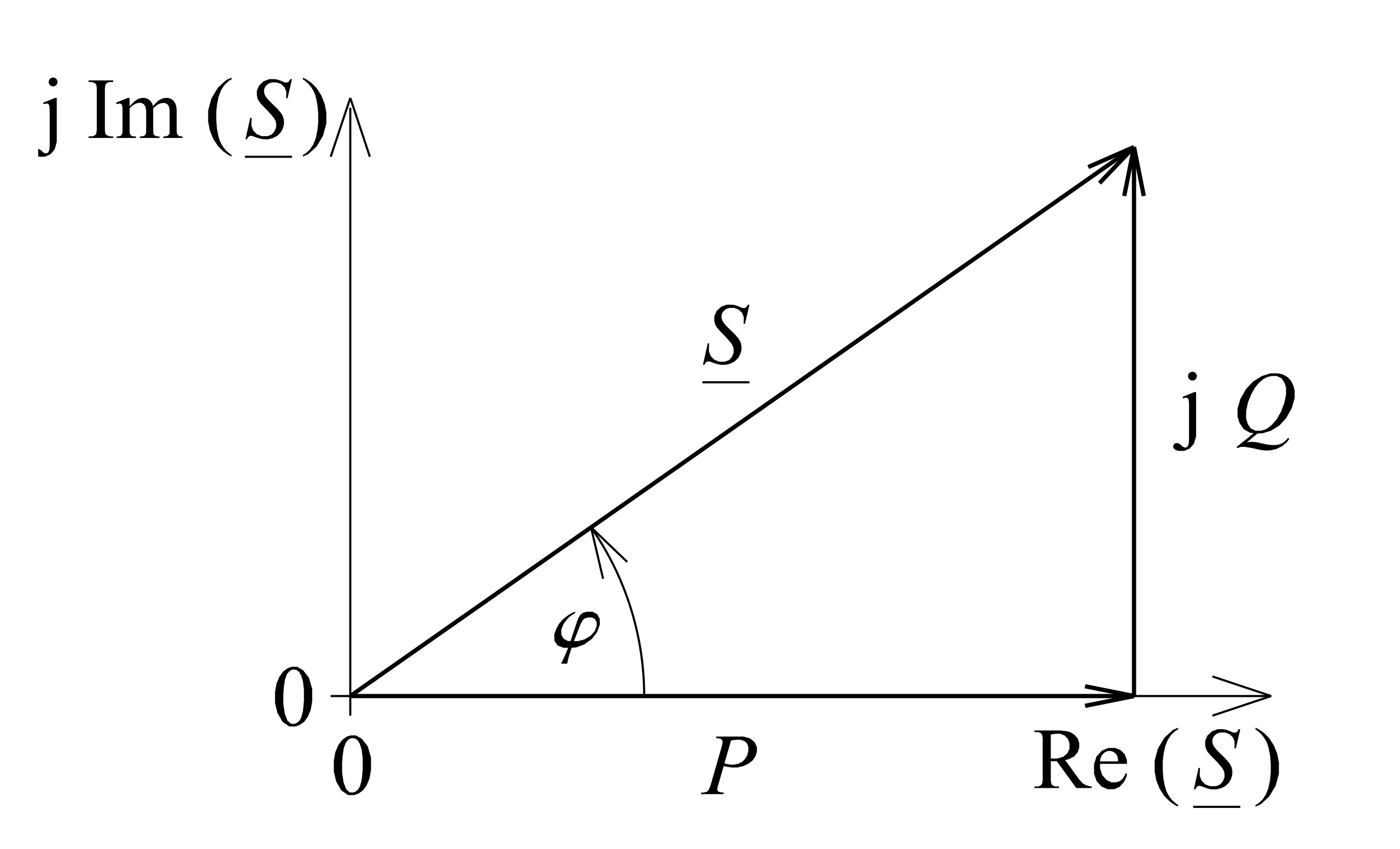
Leistung-PQS-Zeiger.svg von Saure ist CC BY-SA 3.0 gekennzeichnet Das oben abgebildete Zeigerdiagramm verdeutlicht nochmal den Zusammenhang zwischen den drei Größen. Der Phasen(verschiebungs)winkel
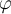 zwischen den Leistungen entspricht dem
zwischen den Leistungen entspricht dem 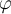 welches wir schon durch die Verschiebung zwischen Strom
und Spannung kennen.
welches wir schon durch die Verschiebung zwischen Strom
und Spannung kennen. - Widerstand
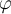 = 0°
= 0°  nur Wirkleistung
nur Wirkleistung- Spule
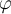 = +90°
= +90°  nur Blindleistung
nur Blindleistung
- Kondensator
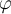 = -90°
= -90°  nur Blindleistung
nur Blindleistung
Bei der Reihen- oder Parallelschaltung von z.B. Spule und Widerstand stellt sich ein bestimmter Winkel
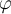 ein, welcher Abhängig vom Verhältnis zwischen R und
ein, welcher Abhängig vom Verhältnis zwischen R und 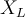 ist.
ist. Beispielrechnung Parallelschaltung:
L = 30 mH
f = 500 Hz
U = 12V
Entsprechend der oberen Abbildung ergibt sich:
Gegenkathete = Imaginärteil =
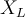 = 94,25
= 94,25 
Ankathete = Realteil = R = 200

= 25,2°
Die Scheinleistung S berechnet sich zu: S =
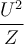 =
= 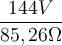
= 1,69 VA
Und für die Wirkleistung gilt:
Und für die Blindleistung:
Kontrollrechnung: S =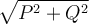 = 1,69 VA
= 1,69 VA
-
Möglichkeiten in der Praxis
Spulen und Kondensatoren finden in quasi jedem elektrischen Gerät Anwendung. Dabei können sie ganz unterschiedliche Aufgaben übernehmen. Einige ausgewählte Anwendungsmöglichkeiten möchte ich dir im Folgenden vorstellen. Bei Interesse kannst du gern selbst mal weiter recherchieren welche Möglichkeiten es noch gibt. 😉
Kondensatoren
Spannungsglättung
Wird eine sinusförmige Wechselspannung durch einen Brückengleichrichter gleichgerichtet werden, vereinfacht gesagt, die negativen Spannungsanteile „nach oben geklappt“. In der Abbildung als graue, gestrichelte Linie dargestellt. Durch die Parallelschaltung eines Kondensators zum Verbraucher kann diese Spannung geglättet werden. Dies wird durch die rote Linie dargestellt. Der Kondensator lädt sich dabei auf Udach auf und entlädt sich dann mehr oder weniger langsam.
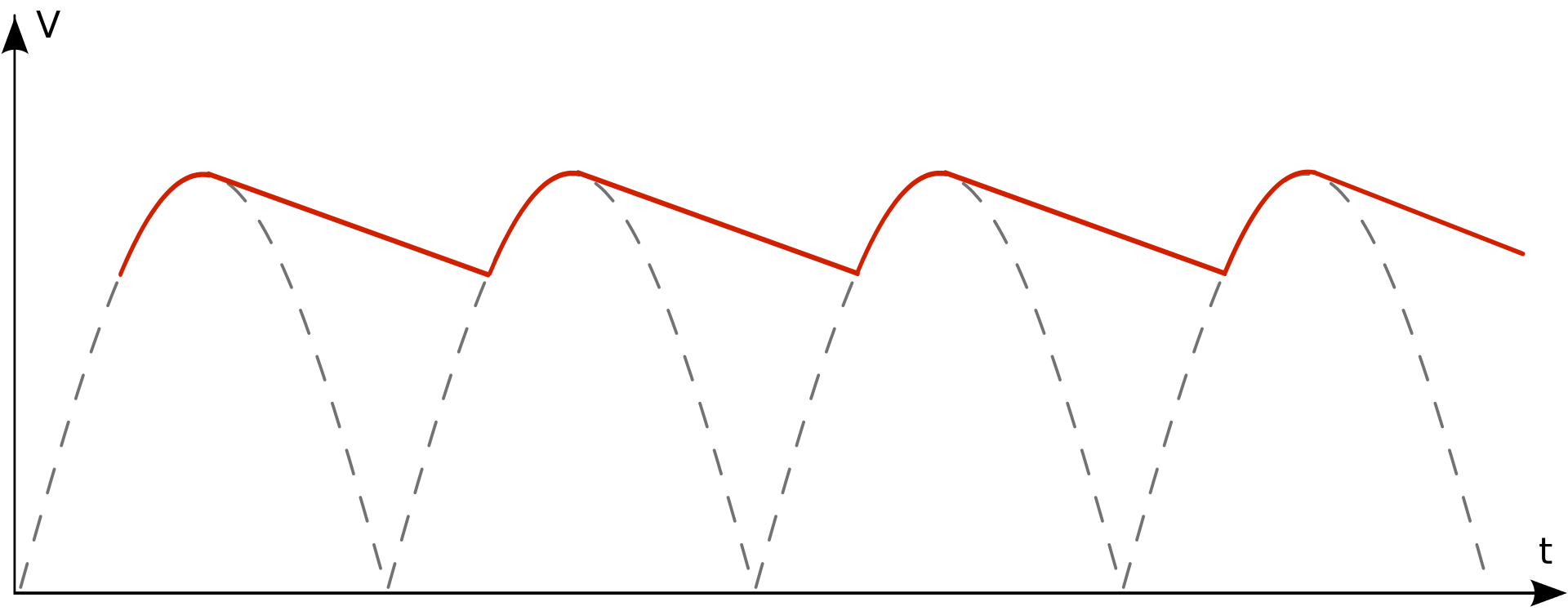
Smoothed_ripple von Spinningspark ist als CC BY-SA3.0 gekennzeichnet
Je nach Kapazität des Kondensators fällt die Glättung besser oder schlechter aus. Bei einem unendlich großen Kondensator, wäre die hier rote Linie eine durchgehende Gerade und wir hätten eine ideale Gleichspannung. Das würde jedoch zu einem sehr großen Strom im Gleichrichter führen. Außerdem kosten große Kondensator mehr Geld und Platz als kleinere, weshalb in der Praxis immer nur ein Kompromiss aus Kosten und Qualität der Glättung gefunden werden muss.
Durch die Reihenschaltung aus Widerstand (R) und Kondensator (C) lassen sich Tief- und Hochpassfilter aufbauen. Diese dienen dazu, hohe (Tiefpass) oder niedrige (Hochpass) Frequenzen aus einem Signal herauszufiltern. Ein entsprechend dimensionierter Tiefpass kann zum Beispiel dazu genutzt werden, hochfrequente Störungen aus einer 50 Hz Versorgungsspannung zu filtern.
Spulen
In Elektromotoren wird die magnetische Kraft genutzt, um den Rotor im Stator zu drehen. Dies kann je nach Motor mit einem Wechselstrom, 3-Phasen-Drehstrom oder mit Gleichstrom geschehen.
Gleichstromsteller
Hoch- und Tiefsetzsteller sind Schaltungen, die dazu in der Lage sind, die Spannungshöhe einer angelegten Gleichspannung zu erhöhen oder herabzusetzen. Siehe auch https://de.wikipedia.org/wiki/Abw%C3%A4rtswandler oder https://de.wikipedia.org/wiki/Aufw%C3%A4rtswandler. Spulen sind für deren Funktion essentiell.
Spulen und Kondensatoren in Kombination
Durch Kombination von Spulen und Kondensatoren lassen sich Frequenzweichen aufbauen wie sie beispielsweise in Lautsprechern zum Einsatz kommen. Das Eingangssignal, in diesem Falle die Musik, hat einen Frequenzbereich von etwa 20 Hz bis 20 kHz. In einer 3-Wege Lautsprecherbox teilt die Frequenzweiche die Musik mit Hilfe verschiedener Filter auf den Hoch-, Mittel- und Tieftöner so auf, dass jeder Einzellautsprecher nur seine Frequenzen bekommt.