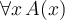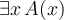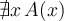7. Zeichen und Formeln
Abschnittsübersicht
-
-
7.1 Hoch- und Tiefstellung
-
7.2 Brüche
-
7.3 Matrizen
Matritzen sin eine erwähnenswerte Ausnahme von der bisherigen TeX-Logik, da sie in speziellen - mit\begineingeleiteten und mit\endbeendeten - Umgebungen notiert werden. Wie auch in den weiter unten folgenden Beispielen zu mehrzeiligen Gleichungen werden die einzelnen Zeilen mit einemm Doppel-Backslash \\ voneinander getrennt. Die Elemente je Zeile werden mit einem & getrennt.
Beispiel:
$$ \begin{pmatrix} x & y \\ z & v \end{pmatrix} $$führt zuFür größere Felder kann es sich anbieten, den TeX-Code in mehreren Zeilen zu notieren (was wiederum höhere Übersichtlichkeit, aber evtl. andere Probleme mit sich bringt. Siehe dazu den Abschnitt "Tipps, Tricks, Troubleshooting"):
$$ \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix} $$
Matrizen ohne Klammern:$$ \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} $$führt zu
Kleine Matrizen ohne Klammern:
$$ \begin{smallmatrix} a & b \\ c & d \end{smallmatrix} $$führt zu
Matrizen mit runden Klammern:
$$ \begin{pmatrix} x & y \\ z & v \end{pmatrix} $$führt zu
Matrizen mit eckigen Klammern:
$$ \begin{bmatrix} 1 & 2 \\ 3& 4 \end{bmatrix} $$führt zu
Matrizen mit geschweiften Klammern:
$$ \begin{Bmatrix} x & y \\ z & v \end{Bmatrix} $$führt zu
Matrizen mit (Betrags-) Strichen:
$$ \begin{vmatrix} x & y \\ z & v \end{vmatrix} $$führt zu
Matrizen mit (doppeltn, Norm-) Strichen:
$$ \begin{Vmatrix} x & y \\ z & v \end{Vmatrix} $$führt zu
Sonderfälle und besondere Darstellungen:
Eine Matrix mit abgetrennten Bereichen oder Blöcken kann man auf verschiedene Weise generieren, z.B.
Eine Matrix mit Punkten als Platzhalter für Reihen kann man mit \cdots, \ddots und \vdots (für horizontale, diagonale und vertikale Punkte) generieren, z.B.
-
7.4 Mathematische Formelzeichen
-

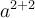
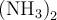
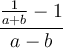
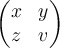
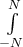
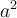
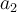
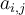
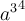
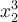
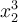
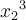
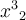
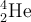
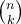
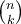
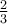
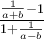
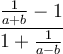
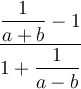
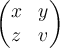
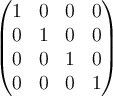
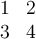
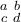

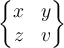
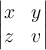
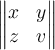
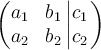
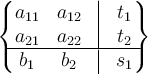

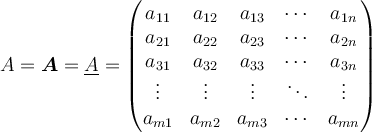
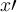
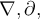
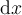
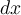
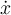
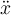
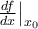
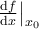
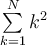
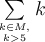
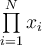
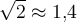
![\sqrt[n]{x} \sqrt[n]{x}](https://moodle.thga.de/filter/tex/pix.php/13fcbed8bcac58d95c0cb989f3aca2de.png)
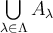
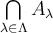
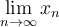
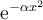
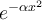
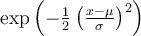
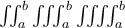
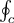
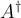
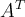
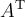
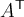
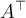
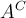
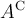
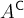
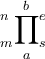
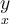
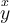
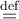
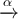
![A \xleftarrow[P+1]{n+\mu-1} B \xrightarrow[T]{n\pm i-1} C A \xleftarrow[P+1]{n+\mu-1} B \xrightarrow[T]{n\pm i-1} C](https://moodle.thga.de/filter/tex/pix.php/63dac46554dfdf1f3007f6857b65f46c.png)