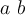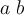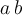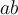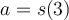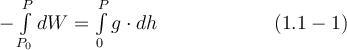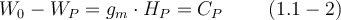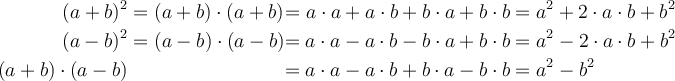8. Formatierungen, Verschachtelungen, Tabellen
Section outline
-
Wenn man mit den obigen Erläuterungen alle benötigten Zeichen darstellen kann, können diese zu komplexen Formeln zusammengesetzt werden. Um diese Formeln zu "setzen", stehen verschiedene Formatierungsmöglichkeiten zur Verfügung:
-
8.1 Leerzeichen
Um Leerzeichen, welche in TeX normalerweise ignoriert werden, zu erzwingen, stehen fünf vergrößerte Zeichenabstände (und ein verringerter Zeichenabstand) zur Verfügung.
Damit kann man in einer Zeile bestimmte Teile innerhalb einer TeX-Notation abrücken:
Beispiel 1 Syntax: Für den freien Fall einer Masse
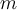 sei das Weg-Zeit-Gesetz
sei das Weg-Zeit-Gesetz$$s=s(t)=s_0-\frac 12 \cdot t^2\qquad mit \qquad s_0=125 \qquad und \qquad g=10$$.Mit den verschiedenen Abständen kann man auch Formeln nummerieren, allerdings ist z.B. die Rechtsbündigkeit der Formelnummerierung im folgenden Beispiel eher "Versuch und Irrtum", da hier z.B: $$\quads$$ mit $$\ $$ kombiniert werden müssen, bis die Abstände stimmen.
Besser geht das in den align- bzw. alignat-Umgebungen, die in den nächsten Abschnitten 8.2 und 8.3 erläutert werden.Beispiel 2 (Formelnummerierung): Syntax: Für die Potentialdifferenz zwischen dem Punkt P (in der Niveaufläche mit dem Potential WP gelegen) und dem Punkt P0 auf dem Geoid (in der als Nullniveau definierten Potentialfläche W0 gelegen) erhält man analog
also
oder
$$ - \int\limits_{P_0}^{P} dW = \int\limits_0^P g \cdot dh \qquad\qquad\qquad(1.1-1)$$
also$$ W_0 - W_P = g_m \cdot H_P = C_P \qquad \ (1.1-2)$$
oder$$ H_P = \dfrac {W_0 - W_P} {g_{\tilde{m}}} \qquad\qquad\qquad \ \ (1.1-3)$$Um ein Gefühl für die einzelnen Abstände zu bekommen, hier eine kleine Hilfestellung:
-
8.2 Ausrichtung mehrzeiliger Gleichungen
Wenn man Rechenschritte oder mehrteilige Gleichungen abbilden möchte, sollten die Gleichheitszeichen der einzelnen Zeilen um der Konvention und der Übersichtlichkeit Willen untereinander stehen.
- Die entsprechenden Einrückungen erreicht man über einen {align}-Bereich, der mit \begin{align} eingeleitet und mit \end{align} beendet wird.
- Jede Zeile innerhalb der align-Umgebung wird mit einem Doppelbackslash (\\) beendet. Die letzte Zeile benötigt kein Endsymbol.
- Die Stellen der Gleichung, welche jeweils aneinander ausgerichtet sein sollen, kennzeichnet man mit einem &-Symbol.
- Die Zeilennummerierung wird automatisch hinzugefügt, können aber unterdrückt werden.
Im ersten Beispiel wird die linke Seite der Gleichung ab Zeile 2 nicht wiederholt, jede Zeile startet also sofort mit dem &=, so dass die Gleichheitszeichen untereinander stehen, links vom Gleichheitszeichen ab der zweiten Zeile aber "nichts" dargestellt wird.
Gleichheitszeichen untereinander, links "leer": Syntax 
$$ \begin{align}
a&=b+c\\
&=5+7\\
&=12
\end{align} $$Im zweiten Beispiel sieht man, dass Teile der Formel links von der &-Markierung rechtsbündig und rechts von der &-Markierung linksbündig dargestellt werden.
Gleichheitszeichen untereinander: Syntax 
$$\begin{align}
1.234^2&=1.522.756\\
123^2&=15.129\\
12^2&=144\\
9^2&=81
\end{align}$$Das dritte Beispiel zeigt, dass nicht nur Gleichheitszeichen, sondern auch andere Zeichen jeder Zeile mittels & aneinander ausgerichtet werden können.
Rechenzeichen untereinander: Syntax 
$$ \begin{align}
a*b&+x\\
c&+x\\
(a+c)^2*b&+x
\end{align} $$Zeilennummerierung unterdrücken
Um die automatische Zeilennummerierung zu unterdrücken, kann {align*} benutzt werden:
Zeilennummerierung unterdrückt: Syntax 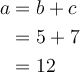
$$ \begin{align*}
a&=b+c\\
&=5+7\\
&=12
\end{align*} $$Ausnahmen in der Zeilennummerierung
Um einzelne Zeilennummern zu unterdrücken, können innerhalb von der {align}-Umgebung (mit automatischer Nummerierung) einzelne Zeilen vor dem beendenden \\ mit dem Befehl \notag versehen werden. Diese Zeilen werden in der Nummerierung übersprungen. Ab der nächsten Zeile wird weitergezählt.
Gleichheitszeichen untereinander, einzelne Zeilennummerierungen unterdrücken: Syntax 
$$ \begin{align}
a&=b+c\\
&=5+7\notag\\
&=12
\end{align} $$Analog können in der {align*}-Umgebung (ohne automatische Nummerierung) einzelne Zeilen gekennzeichnet werden, indem ans Zeilenende vor den \\ ein \tag{...} angegeben wird. So können z.B. wichtige Zwischenergebnisse gekennzeichnet werden, auf die z.B. im Text weiter eingegangen wird.
Gleichheitszeichen untereinander, einzelne Zeilennummerierungen erzwingen: Syntax 
$$ \begin{align*}
a&=b+c\\
&=5+7\tag{q.e.d.}\\
&=12
\end{align*} $$ -
8.3 Mehrzeilige Gleichungen (für Fortgeschrittene)
Die {align}-Umgebung kann mehrere Zeichen nur an einer Stelle aneinander ausrichten. Sollen mehrere Blöcke ausgerichtet werden, muss die {alignat}-Umgebung genutzt werden. In einem weiteren Parameter wird angegeben, wieviele Teile jede Zeile besitzen soll.
Im ersten Beispiel wird also über \begin{alignat} der Bereich eingeleitet und über die folgende {3} angegeben, dass jede Zeile drei Teile besitzt: Der erste reicht bis zum Gleichheitszeichen (&=), der zweite bis vor das erzwungene großen Leerzeichen (&\qquad). Die zweite und die dritte Zeile wird über die jew. &s an der oberen Zeile ausgerichtet und benötigt die Angabe des \qquad nicht mehr zwingend.
Im zweiten Beispiel sehen Sie, wie über ein weiteres &-Zeichen die Ausrichtung (Rechts- und Linksbündigkeit) der einzelnen Formelteile manipuliert werden kann:
Zeilennummerierung unterdrücken, mehrere Blöcke ausrichten
Auch in der {alignat}-Umgebung kann mit einem * die Zeilennummerierung unterdrückt werden: Innerhalb von {alignat} werden mit \notag versehene Zeilen nicht nummeriert bzw. können innerhalb von {alignat*} mit \tag{...} zusätzliche Kennzeichnungen hinzugefügt werden.
Ein letztes Beispiel - nun mit vier Abschnitten (also {alignat*}{4}) - soll verdeutlichen, wie ein Teil einer Zeile ausgelassen werden kann, wenn z.B. die verschiedenen Zeilen unterschiedlich viele Rechenschritte beinhalten. Die Positionierung der &-Zeichen beeinflusst, ob und welche Ausrihtungszeichen (hier: Gleichheitszeichen) angezeigt werden:
-
8.4 Tabellen
Um eine Tabelle in TeX zu erstellen, kann die {array}-Umgebung genutzt werden.
- Nach dem einleitenden \begin{array} wird in geschweiften Klammern definiert, wie die Spalten voneinander abgetrennt sein sollen. {|c||c|c|c|} erzeugt dabei vier Spalten, wobei die erste rechts durch eine doppelte Linie || begrenzt wird.
- Die Zelleninhalte einer Zeile werden hintereinander weg notiert, wobei die Zellen jeweils mit einem &-Zeichen getrennt werden.
- Horizontale Linien können mit dem Befehl \hline zwischen den jeweiligen Zeilen platziert werden.
- Das Ganze muss über ein \end{array} geschlossen werden:
Da die erste Zelle der Kopfzeile leer ist, beginnt die erste Zeile direkt mit einem & und dann mit dem Inhalt der zweiten Zelle:
Syntax Ergebnis $$ \begin{array}{|c||c|c|c|}
& \text{Spalte1} & \text{Spalte2} & \text{Spalte3}\\
\hline
\text{Zeile1} & 1 & 2 & 3\\
\text{Zeile2} & 1 & 2 & 3\\
\text{Zeile3} & 1 & 2 & 3\\
\end{array} $$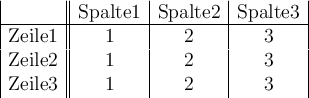
-