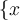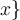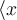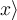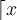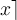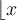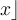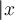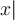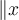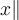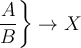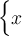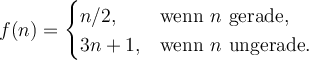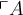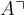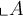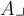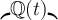4. Klammern und Begrenzungssymbole
Abschnittsübersicht
-
-
4.1 Klammern und Begrenzungssymbole allgemein
Runde Klammern können einfach über die Tastatur eingegeben werden,
$$f(x)$$ führt also zu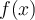
Eckige Klammern werden ebenfalls einfach eingegeben,
$$[A]$$ ergibt![[A] [A]](https://moodle.thga.de/filter/tex/pix.php/7e2bf8880d46cb84f91d8740b2659a88.png)
Alternativ funktinieren die Befehle $$\lbrack ... \rbrack$$:

Geschweifte Klammern können über die Tastatur eingegeben werden, müssen aber mit \ eingeleitet werden:
$$\{...\}$$ führt zu
Alternativ funktinieren die Befehle $$\lbrace ... \rbrace$$:

Spitze Klammern werden mit
$$\langle ... \rangle$$ generiert:
Nicht empfohlen ist die Tastatureingabe von $$ < ... > $$, diese sind eher für Grüßenverhältnisse ('größer als', 'kleiner als') zu nutzen:

Rundungsklammern: Für Auf- und Abrundungsfunktionen steht
$$\lceil x \rceil$$ bzw. $$\lfloor x \rfloor$$ zur Verfügung: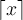 bzw.
bzw. 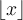
Betragsstriche erstellt man am einfachsten mit $$|-2|$$:
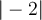
Alternativ stehen die Befehle $$\vert -2 \vert$$ und $$\left|-2\right|$$ zur Verfügung:
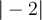 ,
, 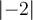
Normstriche benötigen einen zusätzlichen \, also z.B. $$\|-2\|$$:
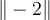
Alternativ stehen die Befehle $$\Vert -2 \Vert$$ zur Verfügung:
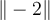 Grundsätzlich ist bei TeX-Befehlen auf Groß- und Kleinschreibung zu achten, hier an \vert und \Vert gut sichtbar. Das gilt aber auch für z.B. \gamma und \Gamma (s. "Liste griechische Buchstaben") oder \bigl und \Bigl (s. "Größenvariable Symbole").
Grundsätzlich ist bei TeX-Befehlen auf Groß- und Kleinschreibung zu achten, hier an \vert und \Vert gut sichtbar. Das gilt aber auch für z.B. \gamma und \Gamma (s. "Liste griechische Buchstaben") oder \bigl und \Bigl (s. "Größenvariable Symbole"). -
4.2 Größenvariable Symbole (autom. Anpassung)
Wenn man einen "hohen" Formelbestandteil, z.B. einen Doppelbruch, mit Begrenzungssymbolen versehen möchte, führen die oben beschriebenen Befehle zu einer nur überschaubar ansehnlichen Darstellung. Beispielhaft sei hier ein (ebenfalls via \dfac statt \frac größenangepasster) Doppelbruch eingeklammert,
$$(\dfrac{\dfrac 1x}{\dfrac{y}{263}})$$:Diese viel zu kleinen Klammern kann man mittels \left( und \right) anpassen,
$$\left( \dfrac{\dfrac 1x}{\dfrac{y}{263}} \right)$$ führt zuDie Zusätze \left und \right funktionieren auch mit allen anderen Klammer- und Begrenzungssymbolen:
Eckige Klammern:
$$\left[ ... \right]$$ führt zu![\left[ \dfrac{\dfrac 1x}{\dfrac{y}{263}} \right] \left[ \dfrac{\dfrac 1x}{\dfrac{y}{263}} \right]](https://moodle.thga.de/filter/tex/pix.php/ae19a076e3976fc2d54ec0fb885ec0f4.png)
Alternative $$\left\lbrack ... \right\rbrack$$ führt zu
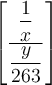
Geschweifte Klammern:
$$\left\{ ... \right\}$$ führt zu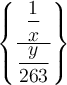
Alternative $$\left\lbrace ... \right\rbrace$$ führt zu
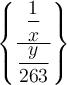
Spitze Klammern:
$$\left\langle ... \right\rangle$$ führt zu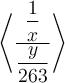
-
4.3 Größenvariable Symbole (manuelle Anpassung)
Klammern können auch manuell in der Höhe angepasst werden. Über eine vierstufige Größenangabe (big, Big, bigg, Bigg) und eine Richtungsangabe (l, r) können die Höhen der Zeichen angegeben werden. Beispiele für runde Klammern:
$$\bigl( ... \bigr)$$führt zu ,
,$$\Bigl( ... \Bigr)$$führt zu ,
,$$\biggl( ... \biggr)$$führt zu , und
, und$$\Biggl( ... \Biggr)$$führt zu .
.
Runde Klammern:
$$\bigl( \Bigl( \biggl( \Biggl( ... \Biggr) \biggr) \Bigr) \bigr)$$
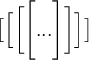
Eckige Klammern:
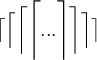
$$\bigl[ \Bigl[ \biggl[ \Biggl[ ... \Biggr] \biggr] \Bigr] \bigr] $$Alternative
$$\bigl\lbrack \Bigl\lbrack \biggl\lbrack \Biggl\lbrack ... \Biggr\rbrack \biggr\rbrack \Bigr\rbrack \bigr\rbrack $$
Geschweifte Klammern:
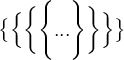
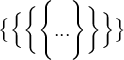
$$\bigl\{ \Bigl\{ \biggl\{ \Biggl\{ ... \Biggr\} \biggr\} \Bigr\} \bigr\}$$Alternative
$$ \bigl\lbrace \Bigl\lbrace \biggl\lbrace \Biggl\lbrace ... \Biggr\rbrace \biggr\rbrace \Bigr\rbrace \bigr\rbrace $$
Spitze Klammern:
$$\bigl\langle \Bigl\langle \biggl\langle \Biggl\langle ... \Biggr\rangle \biggr\rangle \Bigr\rangle \bigr\rangle $$
Rundungsklammern:
$$\bigl\lceil \Bigl\lceil \biggl\lceil \Biggl\lceil ... \Biggr\rceil \biggr\rceil \Bigr\rceil \bigr\rceil $$$$\bigl\lfloor \Bigl\lfloor \biggl\lfloor \Biggl\lfloor ... \Biggr\rfloor \biggr\rfloor \Bigr\rfloor \bigr\rfloor $$
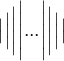
Betragsstriche:
$$\bigl| \Bigl| \biggl| \Biggl| ... \Biggr| \biggr| \Bigr| \bigr|$$Alternative
$$ \bigl\vert \Bigl\vert \biggl\vert \Biggl\vert ... \Biggr\vert \biggr\vert \Bigr\vert \bigr\vert $$
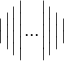
Normstriche:
$$\bigl\| \Bigl\| \biggl\| \Biggl\| ... \Biggr\| \biggr\| \Bigr\| \bigr\|$$Alternative
$$ \bigl\Vert \Bigl\Vert \biggl\Vert \Biggl\Vert ... \Biggr\Vert \biggr\Vert \Bigr\Vert \bigr\Vert $$ -
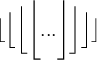
4.4 Klammer-Sonderformen, einseitige Begrenzer
Mit \lgroup und \rgroup stehen "gerade Klammern" zur Verfügung: Der Vergleich von
$$\left\lgroup a \right\rgroup $$ und $$\left( a \right) $$ zeigt die unterschiedliche Darstellung:Einsatzzenarien können mehrzeilige Darstellungen (z.B. Matritzen, mehr unter Zeichen und Formeln) sein:
$$\left\lgroup \begin{matrix} x & y \\ z & v \end{matrix} \right\rgroup$$
Für einseitige Klammern kann ein Punkt als "Platzhalter" genutzt werden: Ein \left. oder \right. führt zur Auslassung des entsprechenden Klammerzeichens:
$$\left( x \right. $$ bzw. $$\left. x \right) $$ führen zuDie Platzhalter funktionieren auch mit den eckigen, geschweiften, spitzen und Rundungsklammern sowie Betrags- und Normstrichen:
Einsatzbeispiel für einseitige Abgrenzer:
$$\left. \dfrac AB \right\} \to X $$ führt zu
Eine weitere Variante einseitiger Begrenzungssymbole (links) sind Fallunterscheidungen via \begin{cases} und \end{cases}:
$$ \begin{cases} x \end{cases} $$ führt zuEinsatzbeispiel für eine Fallunterscheidung:
$$ f(n) =\begin{cases}
n/2, & \text{wenn }n\text{ gerade,} \\
3n+1, & \text{wenn }n\text{ ungerade.}
\end{cases} $$
Ecken können mittels \ulcorner, \urcorner, \llcorner und \lrcorner (u/l = upper/lower + l/r = left/right + corner) generiert werden:
$$\ulcorner A $$,
$$ A \urcorner $$,
$$\llcorner A $$ und
$$\lrcorner A $$ führen zuEine Kombination von je einer linken und rechten Variante ist möglich:
$$\ulcorner A \urcorner $$ führt zu
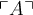 ,
,$$\llcorner A \lrcorner $$ führt zu
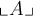 .
.
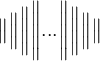
Mit \lmoustache und \rmoustache steht ein weiterer Exot zur Verfügung:
$$\lmoustache \mathbb{Q}(t)\rmoustache$$ führt zu
-

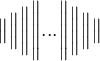
![[ ... ( ... \{ ... \langle ... \vert ... \|... \| ... \vert ...\rangle ... \} ... ) ... ] [ ... ( ... \{ ... \langle ... \vert ... \|... \| ... \vert ...\rangle ... \} ... ) ... ]](https://moodle.thga.de/filter/tex/pix.php/2ee3a7b00474924eae5c488372dca16d.png)
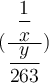
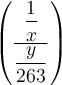
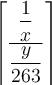
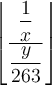
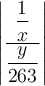
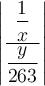
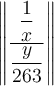
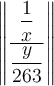
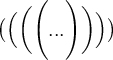
![\bigl[ \Bigl[ \biggl[ \Biggl[ ... \Biggr] \biggr] \Bigr] \bigr] \bigl[ \Bigl[ \biggl[ \Biggl[ ... \Biggr] \biggr] \Bigr] \bigr]](https://moodle.thga.de/filter/tex/pix.php/ff7f81262e9476c0e06cc937a19fb093.png)
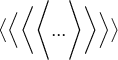
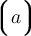
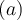
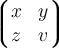
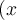
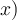
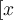
![\left. x \right] \left. x \right]](https://moodle.thga.de/filter/tex/pix.php/c30537bdf9a9fd331f0c16b00d0a72b0.png)