Differentialrechnung

1- Faktorregel: 

Beim Ableiten, bleibt ein konstanter Faktor unverändert erhalten. 

Formel:

$f(x)=k \cdot g(x) \rightarrow f^\prime(x)=k \cdot g^\prime(x)$

Beispiel:

$f(x) = 4 \cdot x^3$

Die Funktion f(x) lässt sich in der Form schreiben: 

$f(x)= 4 \cdot g(x)$ mit $g^\prime(x) = 3x^2$

Da der konstante Faktor 4 erhalten bleibt, erhalten wir die Ableitungsfunktion: $f^\prime(x) = 4 \cdot (3x^2)$
                                   $f^\prime(x) = 12 \cdot x^2$

2- Summenregel:

Bei einer Funktion, die aus einer Summe aus zwei oder mehreren Funktionen besteht, wird die Ableitung gebildet, indem man jede Funktion einzeln ableitet und diese am Ende einfach addiert.

Formel:

$f(x) = m(x) + n(x) \rightarrow f^\prime(x) = m^\prime(x) + n^\prime(x)$

Beispiel:

$f(x) = cos(x) + sin(x)$

Mithilfe der Summenregel, können wir die Funktion f(x) in den zwei Teilfunktionen m(x) und n(x) zerlegen, die wir dann einzeln betrachten können:

$m(x) = cos(x)$ und $n(x) = sin(x)$

Die Ableitungen der Teilfunktionen sind dann : 

$m^\prime(x) = -sin(x)$ und $n^\prime(x) = cos(x)$

Wir erhalten somit die Ableitungsfunktion: $f^\prime(x) = -sin(x)+cos(x)$

3- Potenzregel:

Bei einer Potenzfunktion, wird die Ableitungsfunktion gebildet, indem der Exponent als Vorfaktor runtergesetzt und dieser um -1 verringert wird.

Formel:

$f(x) = x^n \rightarrow f^\prime(x) = n \cdot x^{n-1}$

Beispiel:

$f(x) = x^5$

Die Potenzfunktion f(x) hat als Exponent die Zahl 5.
Bei der neuen Ableitungsfunktion steht die 5 als Vorfaktor. Der neue Exponent ist der um -1 verringerte alte Exponent. Also in diesem Fall eine 4. 

Wir erhalten dann die folgende Ableitungsfunktion:  $f^\prime(x) = 5 \cdot x^4$

4- Produktregel:

Bei einer Funktion, die aus einem Produkt aus zwei oder mehreren Funktionen besteht, können die Faktoren einzeln betrachtet werden.

Formel:

$f(x) = g(x) \cdot k(x) \rightarrow f^\prime(x) = g^\prime(x) \cdot k(x) + g(x) \cdot k^\prime(x)$

Beispiel:

$f(x) = arctan(x) \cdot (4x^3)$

Die Funktion f(x) können wir in den zwei Funktionen g(x) und k(x) zerlegen, die wir einzeln ableiten:  

$g(x) = arctan(x) \rightarrow g^\prime(x) = \dfrac{1}{1+x^2}$ und $k(x) = 4x^3 \rightarrow k^\prime(x) = 12x^2$

Mithilfe der Produktregel, können wir dann die Ableitungsfunktion f´(x) formulieren: 

$f^\prime(x) = 4x^3 \cdot \dfrac{1}{1+x^2} + arctan(x) \cdot 12x^2$

In diesem Fall wird jeder Faktor abgeleitet und mit den anderen ursprünglichen Faktoren multipliziert. Die Produkte werden dann zusammenaddiert. 

Formel für die Produktregel für 3 Faktoren: 

${f(x) = u(x) \cdot v(x) \cdot w(x) \rightarrow f^\prime(x) = u^\prime(x) \cdot v(x) \cdot w(x) + u(x) \cdot v^\prime(x) \cdot w(x) + u(x) \cdot v(x) \cdot w^\prime(x)}$

Beispiel:

$f(x) = x \cdot e^x \cdot cos(x)$

In unserem Beispiel können die Funktionen $u(x) = x, v(x) = e^x \: und \: w(x) = cos(x)$ identifiziert werden. 

Ihre Ableitungsfunktionen lauten: $u^\prime(x) = 1, v^\prime(x) = e^x \: und \: w^\prime(x) = -sin(x)$.

Wird jede Ableitungsfunktion mit den anderen ursprünglichen Funktionen multipliziert und zusammenaddiert, erhalten wir die so weit wie möglich vereinfachte Ableitungsfunktion: 

$f^\prime(x) = -e^x \cdot (x \cdot sin(x) + (-x - 1) \cdot cos(x))$

5- Quotientenregel:

Bruchfunktionen lassen sich mithilfe der Quotientenregel ableiten.  Hier können wir die Zähler- sowie Nennerfunktion einzeln ableiten und am Ende zusammenfügen. 

Formel:

$f(x) = \dfrac{g(x)}{k(x)} \rightarrow f^\prime(x) = \dfrac{g^\prime(x) \cdot k(x)-g(x) \cdot k^\prime(x)}{k(x)^2}$

Beispiel:

$f(x) = \dfrac{3x^2}{sin(x)}$

Aus der Funktion f(x) können wir die zwei Teilfunktionen g(x) und k(x) identifizieren: 

$g(x) = 3x^2$ und $k(x) = sin(x)$

Diese können wir dann einzeln ableiten: 

$g^\prime(x) = 6x$ und $k^\prime(x) = cos(x)$

Mithilfe der Quotientenregel können wir nun die Ableitungsfunktion f´(x) bilden: 

$f^\prime(x) = \dfrac{6x \cdot sin(x) - 3x^2 \cdot cos(x)}{sin^2(x)}$

6- Kettenregel:

Zusammengesetzte Funktionen werden mithilfe der Kettenregel abgeleitet. Hier wird die innere Ableitung mit der äußeren Ableitung multipliziert.

Formel:

$f(x) = u(v(x)) \rightarrow f^\prime(x) = u^\prime(v(x)) \cdot v^\prime(x)$

Beispiel: 

$f(x) = ln(3x+4)$

Bei dieser Funktion, solltest du zum Anfang die innere Funktion und die äußere Funktionen identifizieren und diese jeweils ableiten.

In unserem Beispiel, ist die innere Funktion:  $v(x) = 3x+4$ abgeleitet ergibt: $v^\prime(x) = 3$

Die äußere Funktion ist $u(v(x)) = ln(v(x))$ abgeleitet ergibt: $u^\prime(v(x)) = \dfrac{1}{v(x)} = \dfrac{1}{3x+4}$

Beide Ableitungen v´(x) und u´(v(x)) werden nun miteinander multipliziert und ergeben die Ableitungsfunktion: $f^\prime(x) = \dfrac{3}{3x+4}$


In diesem Fall, solltest du jede einzelne Funktion identifizieren und einzeln ableiten. Diese werden dann miteinander multipliziert. 

Formel für die Kettenregel für 3 Verkettungen: 

$f(x) = u(v(w(x))) \rightarrow f^\prime(x) = u^\prime(v(w(x))) \cdot v^\prime(w(x)) \cdot w^\prime(x)$ 

Beispiel: 

Wie lautet die Ableitung der Funktion $f(x) = ln(cos(2x^2))$?

In unserem Fall, ist die Funktion dreifach verkettet: 

$u(v(w(x))) = ln(cos(2x^2))$ 
$v(w(x)) = cos(2x^2)$ 
$w(x) = 2x^2$

Laut der oben genannten Formel sind die folgenden Ableitungen zu bilden: 

$u^\prime(v(w(x))) = \dfrac{1}{cos(2x^2)}$
$v^\prime(w(x)) = -sin(2x^2)$
$w^\prime(x) = 4x$

Diese werden miteinander multipliziert und ergeben die Ableitungsfunktion: 

$f^\prime(x) = \dfrac{-4x \cdot sin(2x^2)}{cos(2x^2)}$


1- Faktorregel: $f(x)=k \cdot g(x) \rightarrow f^\prime(x)=k \cdot g^\prime(x)$

2- Summenregel: $f(x) = m(x) + n(x) \rightarrow f^\prime(x) = m^\prime(x) + n^\prime(x)$

3- Potenzregel: $f(x) = x^n \rightarrow f^\prime(x) = n \cdot x^{n-1}$

4-Produktregel: $f(x) = g(x) \cdot k(x) \rightarrow f^\prime(x) = g^\prime(x) \cdot k(x) + g(x) \cdot k^\prime(x)$

5- Quotientenregel: $f(x) = \dfrac{g(x)}{k(x)} \rightarrow f^\prime(x) = \dfrac{g^\prime(x) \cdot k(x)-g(x) \cdot k^\prime(x)}{k(x)^2}$

6- Kettenregel: $f(x) = u(v(x)) \rightarrow f^\prime(x) = u^\prime(v(x)) \cdot v^\prime(x)$

Die Kurvendiskussion dient dazu, Funktionen zu untersuchen, um ihre geometrischen Eigenschaften wie beispielsweise Nullstellen, Extrempunkte oder Wendepunkte zu bestimmen. 

Kurzschreibweise:

∈	$$$$	Gehört ein Element $\mathrm{<strong>x</strong>}$ einer Menge M an, so schreiben wir x ∈ M. In Worten: $\mathrm{<strong>x</strong>}$ ist Element von M.
∉	$$$$	Gehört ein Element x einer Menge M nicht an, so schreiben wir x ∉ M. In Worten: x ist kein Element von $\mathrm{<strong>M</strong>}$.
∅	$$$$	Es gibt auch eine Menge, die keine Elemente enthält. Diese bezeichnen wir als leere Menge, kurz $\mathrm{<strong>\varnothing </strong>}$.

Je nach Aufgabenstellung sind verschiedene Eigenschaften des Funktionsgraphs gefragt. 

Für eine komplette Kurvendiskussion empfiehlt es sich aber folgende Schritte zu folgen

Der Definitionsbereich - oder anders genannt die "Definitionsmenge" - gibt an, welche x-Werte man in eine Funktion einsetzen darf.

Je nachdem um welche Funktion es sich handelt, gelten verschiedene Regeln. Hier ist eine kleine Erinnerung 👇

1.1 Lineare Funktionen können alle x-Werte annehmen. Ihr Definitionsbereich ist $D = \mathbb{R}$. 

1.2 Ganzrationale Funktionen oder Polynome höheren Grades können ebenso alle x-Werte annehmen. Ihr Definitionsbereich lautet $D=\mathbb{R}$. 

1.3 Exponentialfunktionen haben den Definitionsbereich $D=\mathbb{R}$. 

1.4 Wurzelfunktionen

               1.4.1 Bei einer Wurzelfunktion mit geradem Wurzelexponent können nur positive Zahlen einschließlich 0 eingesetzt werden. Ihr Definitionsbereich lautet also: $D=\{x \in \mathbb{R} \: | \: x \geq 0\}$

              1.4.2 Eine Wurzelfunktion mit ungeradem Wurzelexponent ist aber für alle reellen Zahlen definiert. Ihr Definitionsbereich ist: $D = \mathbb{R}$.

1.5 Bei gebrochenrationalen Funktionen darf der Nenner nicht gleich 0 sein. Dadurch entstehen sogenannte Definitionslücken, wo die Funktion eine Polstelle oder anders genannt "vertikale Asymptote" hat. 

1.6 Bei Logarithmusfunktionen dürfen nur positive Zahlen ausschließlich (ohne) 0 eingesetzt werden. Ihr Definitionsbereich lautet: $D=\{x \in \mathbb{R} \: | \:x>0\}$

Bei einer Funktion, die aus mehreren Funktionstypen besteht, solltest du darauf achten, dass der gesamte Definitionsbereich alle einzelnen Definitionsmengen umfasst. 

Beispiel: 

Bestimme den Definitionsbereich der Funktion: $f(x)=\dfrac{\sqrt{x^2}}{ln(2-x)}$.

In unserem Beispiel kommen Bruch, Wurzel und Logarithmus in der Funktion vor. Dementsprechend sind alle Bedingungen zu beachten: 

• Der Nenner darf nicht 0 sein, d.h $ln(2-x)\neq0$ -> $2-x \neq e^0$ ->  $x\neq1$
• Der Radikand darf nie kleiner als Null sein, d.h $x^2\geq0$. Hier gibt es also keine Einschränkung. 
• In einer Logarithmusfunktion sind nur positive Zahlen ausschließlich 0 zulässig, d.h $2-x>0$ -> $x$ 

Für den gesamten Definitionsbereich der Funktion f(x) müssen alle Einschränkungen berücksichtigt werden. 

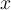
Mithilfe eines Zahlenstrahls, lässt sich die Definitionsmenge anschaulicher visualisieren: 

Der endgültige Definitionsbereich lautet $D = (-\infty;1)\cup(1;2)$

Mit dem Wertbereich oder genannt auch Wertmenge kannst du bestimmen, welche Y-Werte eine Funktion annimmt.
W_f ist die Kennzeichnung für Wertebereich einer Funktion f(x).

Damit du das nachvollziehen kannst, schau vielleicht dieses Video .

Als Nächstes sind die Schnittpunkte mit den Koordinatenachsen zu ermitteln. 

Um die Schnittpunkte mit der x-Achse oder anders genannt "Nullstellen" zu berechnen, wird die Funktion gleich 0 gesetzt: 

$f(x)=0$

Um die Schnittpunkte mit der y-Achse zu berechnen wird x = 0 in der Funktion eingesetzt:

$f(0)=y$

Beispiel:  

An welchen Punkten schneidet sich die folgende Funktion $f(x)=x^2-3x+2$ mit den Koordinatenachsen? 

Um die Nullstellen zu berechnen, wird die Funktion gleich 0 gesetzt. 

Bei unserer Funktion, handelt es sich um eine quadratische Gleichung. 

Ihre Nullstellen lassen sich mit unterschiedlichen Methoden (ABC-Formel, PQ-Formel, Lösen mit binomischen Formeln ...) berechnen. 

Wir erhalten: 

$x_1=1$ und $x_2=2$

Unsere Funktion hat also folgende Nullstellen S_x1(1|0) und S_x2(2|0).

Um den Schnittpunkt mit der y-Achse zu bestimmen, wird x=0 eingesetzt : 

$f(0)=0^2-3\cdot0+2=2$

Unsere Funktion schneidet die y-Achse also an der Stelle Sy(0|2).

1. Lineare Funktion:
Beispiel: f(x) = 2x – 4
0 = 2x – 4      |+4
4 = 2x            |:2
2 = x

2. Linearfaktoren
0 = (x – 4)∙(x+3)
x – 4 = 0 oder x + 3 = 0
⇒ x₁ = 4,   x₂ = -3

3. Rein quadratische Funktion
Beispiel: f(x) = x² – 4
 0 = x² – 4
 0 = (x+2)∙(x–2)
 ⇒ x₁ = -2,   x₂ = 2

4. Quadratische Funktion ohne Konstante
Beispiel: f(x) = x² – 4x
 0 = x² – 4x
 0 = x ∙ (x– 4) ⇒
x₁ = 0,    x₂ = 4

5. Quadratische Funktion
Beispiel: f(x) = x² – 8x + 12
 pq-Formel: Voraussetzung: 0 = x² + px + q
$x_1,_2 = - \frac{p}{2} \pm \sqrt[]{( \frac{p}{2} )^2-q} = - \frac{-8}{2} \pm \sqrt[]{( \frac{-8}{2} )^2-12}$
$= 4 \pm \sqrt[]{4} = 4\pm2$
$\Rightarrow x_1=6 , x_2=2$


abc-Formel: Voraussetzung: 0 = ax² + bx + c
$x_1,_2= \frac{-b \pm \sqrt[]{b^2-4ac} }{2a} = \frac{-(-8)\pm \sqrt[]{8^2-4*1*12} }{2*1}$
$= \frac{8\pm \sqrt[]{16} }{2} = \frac{8\pm4}{2}$
$\Rightarrow x_1=6, x_2=2$


6. Funktion 4-ten Grades (nur x4 , x2 und Konstante)
Beispiel: f(x) = x4 – 5x² + 4
0 = x⁴ – 5x² + 4
Substitution: 
x² = z
0 = z² – 5z + 4
Lösen mit pq- oder abc-Formel oder quadratischer Ergänzung.
⇒ z₁ = 1, z₂ = 4
Rücksubstitution: z = x²
x² = 1, x² = 4
 ⇒ x₁ = 1, x₂ = -1, x₃ =2, x₄=-2

In diesem Schritt wird die Symmetrie von Funktionen untersucht. Dies kannst du ohne großen Rechenaufwand tun. 

Es gilt: 

$f(-x)=f(x)$ bedeutet, dass die Funktion achsensymmetrisch zur y-Achse ist.

$f(-x)=-f(x)$ bedeutet, dass die Funktion punktsymmetrisch zum Koordinatenursprung ist.

Beispiel1 : 

Die Funktion $f(x)=x^4-x^2-1$ ist auf ihre Achsen- bzw. Punktsymmetrie zu untersuchen.  

Um das Symmetrieverhalten zu bestimmen, wird $-x$ in der Funktion eingesetzt: 

$f(-x)=(-x^4)-(-x^2)-1 = x^4-x^2-1=f(x)$

Dadurch lässt sich feststellen, dass unsere Funktion achsensymmetrisch zur y-Achse ist. 

Beispiel2 :

Welche Symmetrieeigenschaften besitzt die Funktion $f(x)=4x^3 + 6x$ ?

Setzen wir $-x$ in unserer Funktion erhalten wir :

$f(-x) = 4 (-x^3) + 6(-x) =-4 x^3-6x =-(4 x^3+6 x)=-f(x)$

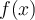Die Funktion $f(x)$ ist somit punktsymmetrisch zum Koordinatenursprung.

Hier wird untersucht, was bei Funktionen passiert, wenn unendlich große oder kleine Werte eingesetzt werden. 

Mathematisch drückt man den Grenzwert einer Funktion an einer bestimmten Stelle mit dem Limes aus. 

Dafür gibt es einige Regeln, durch die du direkt erkennen kannst, wie sich die Funktion im Unendlichen verhält: 

5.1 Bei ganzrationalen Funktionen, entscheidet der Summand mit dem höchsten Exponenten über die Grenzwerte der Funktion. Dabei hängt das genaue Verhalten davon ab, ob der Exponent gerade oder ungerade ist und welches Vorzeichen davor steht. 

Für ganzrationale Funktionen $f(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_0$ gilt: 

Beispiel: 

Wie verhält sich die Funktion $f(x)=-4x^3+2x^2+5x+6$ im positiven sowie negativen Unendlichen ? 

Als Erstes solltest du den Leitkoeffizient und den Funktionsgrad identifizieren. 

In unserem Beispiel handelt es sich um eine ganzrationale Funktion vom Grad 3 mit dem Leitkoeffizient -4. 

Daraus lässt sich ableiten: 

$\lim\limits_{x\to+\infty}f(x)=-\infty$ und $\lim\limits_{x\to-\infty}f(x)=+\infty$

5.2 Bei der Untersuchung von gebrochenrationalen Funktionen unterscheidet man drei Fälle: 

Für den Fall n>m, muss man den Quotient aus dem Leitkoeffzienten $\dfrac{a_n}{b_m}$ von Zähler- und Nennerpolynom untersuchen. Dazu muss man darauf achten, ob die Zahlenwerte n und m beide gerade oder ungerade sind.  

So werden folgende Fälle unterschieden: 

* mit " n und m gleich " ist gemeint, dass n und m beide gerade oder ungerade sind 

* mit " n und m verschieden " ist gemeint, dass n gerade und m ungerade ist, oder umgekehrt  

Beispiel1: 

Wie verhält sich die Funktion $\dfrac{5x^3-7x^2+4}{2x^3+8x+3}$ gegen $\pm\infty$ ? 

Bei der obigen Funktion, haben Zähler und Nenner den gleichen Grad 3. 

Es lässt sich feststellen dass: 

$\lim\limits_{x\to\pm\infty}f(x)=\dfrac{a_n}{b_m}=\dfrac{5}{2}=2,5$ 

Man sagt, dass die Funktion gegen den Wert 2,5 konvergiert. 

Beispiel2: 

Wie verhält sich die Funktion $f(x)=\dfrac{-5x^7-6}{3x^6+4}$ gegen $\pm\infty$ ? 

In diesem Fall lässt sich folgendes feststellen: 

• $n>m$
• $\dfrac{a_n}{b_m}$ 
• n ist ungerade und m ist gerade

Aus der obigen Tabelle lässt sich die Grenzwerte ganz einfach ablesen. 

Wir erhalten dann: 

$\lim\limits_{x\to+\infty}f(x)=-\infty$ und $\lim\limits_{x\to-\infty}f(x)=+\infty$

5.3 Bei Funktionen, wo die " eulersche Zahl e " vorkommt, also die E-Funktion, gelten folgende Regel: 

$\lim\limits_{x\to-\infty}e^x=0$

$\lim\limits_{x\to+\infty}e^x=+\infty$

Ein Beispiel dafür findest du in diesem Video.

5.4 Da Wurzelfunktionen keine negative Werte abbilden, gelten folgende Regel bei der Untersuchung ihrer Grenzwerte: 

Ein Beispiel dafür findest du in diesem Video (siehe Datenschutz-Hinweis oben).

Was ist ein Extrempunkt überhaupt?

Es gibt zwei Arten von Extrempunkte.

            6.01 Hochpunkt: Wenn du versuchst einen Stein möglichst hoch zu werfen, erregend wann wird der Stein wieder Richtung der Boden fallen. 

             Dort wo der Stein vom Steigen ins Fallen wechselt, hast du einen so genannten Hochpunkt .

            6.02 Tiefpunkt: Dann wird der Stein mit der Boden zusammenstoßen und prallt er wieder ab. Dort wo der Rückstoß auftritt ist der Tiefpunkt.

Eine Funktion f(x) hat an der Stelle x_E ein Extremum wenn : $f^\prime(x_E)=0$

Es handelt sich um ein Minimum (Tiefpunkt) wenn: $f^\prime(x_E)=0$ und $f^{\prime\prime}(x_E)>0$

Es handelt sich um ein Maximum (Hochpunkt) wenn: $f^\prime(x_E)=0$ und $f^{\prime\prime}(x_E)$

Anschließend werden die Extremstellen x_E in f(x) eingesetzt um die Extremwerte y_E zu berechnen. 

Beispiel:

Welche Extrempunkte besitzt die Funktion $\dfrac{2}{3}x^3+3x^2+4x$ ?

Als Erstes ist die erste Ableitung zu bilden. Mithilfe der Ableitungsregel erhalten wir: 

$f^\prime(x)=2x^2+6x+4$

Danach wird die erste Ableitung gleich 0 gesetzt, um potenzielle Extremstellen herauszufinden: 

$f^\prime(x)=2x^2+6x+4=0$ liefert folgende Extremstellen x_E1 = -2 und x_E2 = -1. 

Als Nächstes wird die zweite Ableitung gebildet  

$f^{\prime\prime}(x)=4x+6$

wo die Extremstellen x_E1 und x_E2 eingesetzt werden: 

$f^{\prime\prime}(-1)=2>0$ bedeutet,  dass die Funktion f(x) einen Minimum an der Stelle x_E1 = -1 besitzt.

$f^{\prime\prime}(-2)=-2$ bedeutet, dass die Funktion f(x) einen Maximum an der Stelle x_E2 = -2 besitzt.

Anschließend werden die Extremwerte y_E1 und y_E2 bestimmt, indem die Extremstellen x_E1 und x_E2 in f(x) eingesetzt werden: 

$y_{E1}=f(-2)=\dfrac{-4}{3}$ und $y_{E2}=f(-1)=\dfrac{-5}{3}$

Wir erhalten somit die beiden Extrempunkte: $H(-2\:|\:\dfrac{-4}{3})$ und $T(-1\:|\:\dfrac{-5}{3})$

Mit Hilfe der Untersuchung des Monotonieverhaltens einer Funktion kannst du herausfinden, in welchen Bereichen der Funktionsgraph steigt oder fällt. 

Grundsätzlich gibt es zwei Methoden, um das Monotonieverhalten einer Funktion zu bestimmen. Einmal mit der zweiten Ableitung und einmal ohne. 

7.1 Mit der zweiten Ableitung: 

Um das Monotonieverhalten mithilfe der zweiten Ableitung zu bestimmen solltest du folgende Schritte befolgen: 

1. Erste Ableitung berechnen
2. Nullstellen der ersten Ableitung berechnen 
3. Zweite Ableitung berechnen
4. Nullstellen der ersten Ableitung in die zweite Ableitung einsetzen
5. Intervalle bestimmen und Ergebnis zusammenfassen 

Beispiel: 

Bestimme das Monotonieverhalten der Funktion $f(x)=x^2$.

Um dies zu tun, werden wir die oben aufgelistete Schritte befolgen:

1. Erste Ableitung berechnen: $f^\prime(x)=2x$
2. Nullstellen der ersten Ableitung berechnen: $f^\prime(x)=0$ liefert $x=0$ 
3. Zweite Ableitung berechnen: $f^{\prime\prime}(x)=2$
4. Nullstellen der ersten Ableitung in die zweite Ableitung einsetzen: $f^{\prime\prime}(0)=2>0$ . Es handelt sich um einen Tiefpunkt an der Stelle $x=0$.
5. Die berechnete Nullstelle teilt den Definitionsbereich $D=\mathbb{R}$ in zwei Intervalle: 

• Intervall1: $]-\infty;0[$ 
• Intervall2: $]0;+\infty[$ 

Da die Funktion bei x = 0 einen Tiefpunkt besitzt, ist sie im Bereich $]-\infty;0[$ streng monoton fallend und im Bereich $]0;+\infty[$ streng monoton steigend. 

7.2 Ohne zweite Ableitung 

Ähnlich wie bei der ersten Methode, werden hier folgende Schritte befolgt, um das Monotonieverhalten einer Funktion ohne der zweiten Ableitung zu bestimmen: 

1. Erste Ableitung berechnen
2. Nullstellen der ersten Ableitung berechnen 
3. Intervalle aufstellen
4. Monotonietabelle erstellen
5. Vorzeichen der Intervalle ermitteln und Ergebnis angeben

Beispiel: 

Bestimme das Monotonieverhalten der Funktion $f(x)=x^2$

Anhand oben genannter Schritte kannst du das Monotonieverhalten einer Funktion ohne zweite Ableitung ermitteln: 

1. Erste Ableitung berechnen: $f^\prime(x)=2x$
2. Nullstellen der ersten Ableitung berechnen: $f^\prime(x)=0$ liefert $x=0$ 
3. Die berechnete Nullstelle teilt den relevanten Bereich in zwei Intervalle: $]-\infty;0[$ und $]0;+\infty[$
4. In der ersten Zeile der Monotonietabelle stehen die Intervalle. In der zweiten Zeile tragen wir die jeweiligen Vorzeichen, die wir im nächsten Schritt ermitteln werden: 
5. Die Vorzeichen der Intervalle lassen sich ganz einfach berechnen, indem wir eine beliebige Zahl aus dem Intervall in die erste Ableitung einsetzen: 

• Aus dem Intervall $]-\infty;0[$ können wir die Zahl -3 auswählen: $f^\prime(-3)=-6$. Die Funktion f(x) ist in diesem Bereich streng monoton fallend.
• Aus dem Intervall $]0;+\infty[$ können wir die Zahl 3 auswählen: $f^\prime(3)=6>0$. Die Funktion f(x) ist in diesem Bereich streng monoton steigend

So sieht dann die komplette Monotonietabelle aus: 




Welche Methode soll ich anwenden ? 🙄
Je nachdem ob du die zweite Ableitung im weiteren Verlauf einer Aufgabe brauchst oder nicht, kannst du dir selber überlegen, ob du die Methode mit der zweiten Ableitung anwendest.

7.3 Sonderfall: Funktion mit Polstellen: 

Bei Funktionen, die neben Nullstellen auch Polstellen besitzen, musst du diese ebenfalls bei der Bestimmung der Intervalle berücksichtigen. 

Beispiel:

Die folgende Funktion $\dfrac{x^2}{x+1}$ ist auf Ihr Monotonieverhalten zu untersuchen. 
Um das Monotonieverhalten dieser Funktion zu bestimmen, wählen wir die Methode ohne zweite Ableitung aus:

1. Erste Ableitung berechnen: $f^\prime(x)=\dfrac{x^2+2x}{(x+1)^2}$
2. Nullstellen der ersten Ableitung berechnen: $f^\prime(x)=0$ liefert $x_1=-2$ und $x_2=0$
3. In unserem Beispiel handelt es sich um eine gebrochenrationale Funktion, die eine Polstelle an der Stelle x_P = -1 hat. Diese müssen wir ebenso berücksichtigen bei der Bestimmung der Intervalle. So erhalten wir folgende Intervalle: $]-\infty;-2[,]-2;-1[,]-1;0[ \: und \: ]0;+\infty[$

So sieht das Grundgerüst unserer Monotonietabelle aus:   
 

Ähnlich wie beim obigen Beispiel lassen sich die Vorzeichen der Intervalle ermitteln und wir erhalten folgende Monotonietabelle
 

Bei Wendepunkten ändert der Funktionsgraph sein Krümmungsverhalten. Er wechselt an dieser Stelle von einer Rechts- in eine Links-Krümmung oder umgekehrt. 

Die Wendetangente ist die Tangente, welche die Kurve im Wendepunkt schneidet.

Um Wendepunkte zu bestimmen, musst du folgende Schritte befolgen: 

1. Zweite Ableitung bilden.
2. Zweite Ableitung gleich 0 setzen und Nullstellen berechnen.
3. Dritte Ableitung bilden. 
4. Nullstellen der zweiten Ableitung in die dritte Ableitung einsetzen. Wenn die dritte Ableitung dort größer null ist, dann haben wir einen Wechsel von Rechts- nach Links-Krümmung und wenn sie kleiner null ist, dann haben wir einen Wechsel von Links- nach Rechts-Krümmung.
5. x-Werte in f(x) einsetzen, um die y-Koordinate der Wendepunkte zu berechnen

Beispiel: 

Gegeben ist die Funktion f(x)=2x³ -12x²

Frage: 

Welche Wendepunkte besitzt der zugehörige Funktionsgraph ?

Lösung: 

Um die Wendepunkte zu bestimmen, folgen wir den oben genannten Schritten: 

1. Zweite Ableitung bilden: f `(x) = 6x² -24x

                                                  f ``(x) = 12x -24

2. Zweite Ableitung gleich 0 setzen und Nullstellen berechnen: 12x -24 =  0 => x_wp =2                                                                                              
3. Dritte Ableitung bilden: f ```(x) = 12
4. Nullstellen der zweiten Ableitung in die dritte Ableitung einsetzen: f ```(2) = 12 > 0 => Hier wir haben einen Wechsel von Rechts- nach Links-Krümmung.
5. x-Werte in f(x) einsetzen, um die y-Koordinate der Wendepunkte zu berechnen: y_WP = f(2) = -32 => Der Funktionsgraph hat den Wendepunkt WP (2,-32).

Ein weiterer wichtiger Aspekt jeder Kurvendiskussion ist das Krümmungsverhalten. 

Es gilt: 

f ``(x_E)>0 => Der Funktionsgraph ist linksgekrümmt (konvex).

f ``(x_E)<0 => Der Funktionsgraph ist rechtsgekrümmt (konkav)

Beispiel:
Wie ist das Krümmungsverhalten der folgenden Funktion: f(x)=-x⁴/4 +3x²/2 +1 ?
Als Erstes musst du die zweite Ableitung bilden: 
f `(x)= -x³ +3x
f ``(x)= -3x² +3
Die zweite Ableitung wird dann gleich null gesetzt, um die Lösung zu berechnen: -3x²+3 =0
=> x₁=+1 , x₂=-1
Somit erhalten wir drei Intervalle: 

       1. Intervall von -∞ bis -1
       2. Intervall von -1 bis +1
       3. Intervall von +1 bis +∞
Ob der Graph links- oder rechtsgekrümmt ist, lässt sich einfach herausfinden, indem wir in die zweite Ableitung eine beliebige Zahl aus dem Intervall einsetzen: 
Aus dem 1. Intervall wählen wir x_E =-3 aus: f ``(-3)=-3(-3)<sup>2</sup> +3 = -24 => Der Funktionsgraph ist in diesem Intervall rechtsgekrümmt (konkav)
Aus dem 2. Intervall wählen wir x<sub>E</sub> =0 aus: f ``(+3)=-3(0)² +3 = +3 => Der Funktionsgraph ist in diesem Intervall linksgekrümmt (konvex)
Aus dem 3. Intervall wählen wir x_E =+3 aus: f ``(+3)=-3(+3)² +3 = -24 => Der Funktionsgraph ist in diesem Intervall rechtsgekrümmt (konkav)