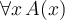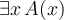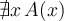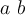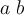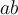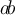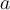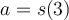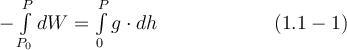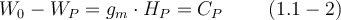10. Formeln mit TeX
Abschnittsübersicht
-
 TeX (Aussprache: 'tech') ist ein Textsatzsystem, welches
in der wissenschaftlichen Welt recht verbreitet ist. So können z.B. wissenschaftliche Paper oder ganze Bücher in einer Auszeichnungssprache (eine sog. 'markup language', die sowohl den eigentlichen Inhalt als auch Befehle zur Darstellung enthält) geschrieben werden, um diese dann z.B. in das PDF-Format zu exportieren. TeX enthält in seiner Grundform ca. 300 Befehle (sogenannte 'primitives') zur Darstellung von Formaten wie 'Überschrift', 'Absatz' oder 'Liste', aber auch für mathematische Formeln. Diese primitives sind über Makrosammlungen erweiterbar; die berühmteste Sammlung ist wahrscheinlich LaTeX.
TeX (Aussprache: 'tech') ist ein Textsatzsystem, welches
in der wissenschaftlichen Welt recht verbreitet ist. So können z.B. wissenschaftliche Paper oder ganze Bücher in einer Auszeichnungssprache (eine sog. 'markup language', die sowohl den eigentlichen Inhalt als auch Befehle zur Darstellung enthält) geschrieben werden, um diese dann z.B. in das PDF-Format zu exportieren. TeX enthält in seiner Grundform ca. 300 Befehle (sogenannte 'primitives') zur Darstellung von Formaten wie 'Überschrift', 'Absatz' oder 'Liste', aber auch für mathematische Formeln. Diese primitives sind über Makrosammlungen erweiterbar; die berühmteste Sammlung ist wahrscheinlich LaTeX.Im engeren Sinn handelt es sich bei TeX und den Makrosammlungen also um eine Software, die in der Lage ist, Anweisungen in Zeichenform in ein Grafik- oder Dokumentformat umzuwandelt. In unserem Moodle ist ebenfalls ein TeX-Filter installiert, welcher (ausgewählte) TeX-Befehle innerhalb anderer Zeichen erkennt und automatisch in Formelzeichen, mathematische Operanden und Sonderzeichen umwandelt. Diese werden als Grafik (PNG mit transparentem Hintergrund) in die Moodle-Seiten eingebunden.
Der TeX-Filter innerhalb des Moodle-Systems hat diverse Vorteile:
- Sie sind in Hypertexten, mit dem Editor angelegten Texten und sonstigen Kursbestandteilen (z.B. Forum, Glossar, Wiki, etc.) verwendbar.
- Sie sind plattform-, browser- und geräteunabhängig nutzbar.
- Erstellung von Formel-Grafiken über einen externen Generator (oder den Office-Formeleditor 🙈), Export und Einbindung der Grafiken entfällt.
- Die Tex-Auszeichnungen bleiben für Autor/innen in einem editierbaren Format, so dass Änderungen schnell machbar sind.
- Betrachter/innen erhalten standardkonforme Darstellungen von Formeln und Sonderzeichen.
Der Nachteil besteht in der notwendigen Syntax der Auszeichnungssprache, die man erlernen muss.Beispiele:
-
TeX funktioniert nach recht einfachen Regeln. Mit ein wenig Übung kann man TeX beinahe fließend schreiben und ist damit deutlich schneller als z.B. mit dem Formeleditor von Office oder dem Moodle-Editor, der nur durch eine Kombination von Maus und Tastatur (Formelteil anklicken, zum Bearbeiten auswählen, Inhalt per Tastatur eingeben) zu bedienen ist. Die Grundregeln, die Ausnahmen von diesen Regeln 🙄, und Moodle-eigene Probleme werden in diesem Kurs erläutert.
-
1.1 Drei Grundregeln zum Einstieg
Um sich der Funktionsweise des TeX-Systems zu nähern (wenn Sie nicht zufällig bereits fließend LaTeX schreiben), kann man sich drei Grundregeln merken:- TeX-Kennzeichnung mit $$
Jeder TeX-Befehl beginnt und endet mit einem "Doppel-Dollar" ($$ Formel $$), so dass der TeX-Filter die mit dieser Kennzeichnung umschlossene Zeichenketten auf spezielle Weise interpretiert und darstellt. - Befehle mit \
Sonder- oder Formelzeichen erzeugt man über spezielle Befehle, die meist mit einem "Backslash" (also:\) beginnen und dahinter einen Kurznamen des gewünschten Formelbestandteils tragen, z.B.\fracfür einen Bruch (von engl. "fraction").
"Normale" Zeichen, wie einzeilige Klammern oder Buchstaben - z.B.f(x)- können ohne\eingegeben werden.
Manche Befehle bestehen aus einzelnen Zeichen, z.B. ^ für Hoch- oder _ für Tiefstellungen und werden ohne \ notiert. - Parameter mit {}
Parameter dieser Befehle werden in geschweiften Klammern (also:{und}) angegeben.
Ein Beispiel:
Einen Bruch definieren Sie mit$$\frac{Zähler}{Nenner}$$. Die Eingabe der Zeichenfolge$$\frac{123}{456}$$ergibt dann folgende Darstellung: Erläuterung:- Ein Doppel-$ (Regel 1) eröffnet und schließt die TeX-konforme Eingabe.
- Danach folgt der TeX-Befehl \frac (Regel 2) zur Generierung eines Bruchs.
- Dieser wird durch Zähler und Nenner, jeweils in geschweiften Klammern (Regel 3), "befüllt".
- TeX-Kennzeichnung mit $$
-
1.2 Ausnahmen und Sonderfälle
Ausnahme 1
"Ein-Zeichen-Parameter" benötigen keine geschweiften KlammernWenn ein Parameter eines TeX-Befehls aus nur einem Zeichen besteht, können (≠ müssen) zur Vereinfachung die geschweiften Klammern weggelassen werden. Dies ist z.B. bei Zählern, Nennern oder Hoch-/Tiefstellungen, die nur aus einem Zeichen (z.B. einer einstelligen Zahl) bestehen, der Fall:
Beispiel Hoch- oder Tiefstellungen:
$$ x^a $$wird zu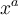
Beispiel Strecken und Vektoren:$$ \overline A $$wird zu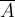 Die Befehle "Hochstellen" (^), "Tiefstellen" (_) und "Linie/Vektorpfeil darüber" (\overline bzw. \overrightarrow) funktionieren in den Beispielen ohne {...}, da die Parameter lediglich aus einem Zeichen bestehen. Die "Langversionen" incl. der Parameter-Klammern (z.B. $$x^{a}$$ oder $$\overrightarrow{A}$$ funktionieren natürlich trotzdem:
Die Befehle "Hochstellen" (^), "Tiefstellen" (_) und "Linie/Vektorpfeil darüber" (\overline bzw. \overrightarrow) funktionieren in den Beispielen ohne {...}, da die Parameter lediglich aus einem Zeichen bestehen. Die "Langversionen" incl. der Parameter-Klammern (z.B. $$x^{a}$$ oder $$\overrightarrow{A}$$ funktionieren natürlich trotzdem: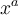 bzw.
bzw. 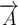
Beispiel Brüche:$$ \frac 12 $$oder auch$$ \frac 1 2 $$wird zu$$ \frac{x+y}2 $$wird zuZähler und Nenner müssen nur in geschweifte Klammern gesetzt werden, wenn sie aus mehr als einem Zeichen bestehen. Da der Befehl \frac zwei Parameter erwartet, kann sogar auf das Leerzeichen (Bsp. 1) verzichtet werden. Wer sich die Arbeit machen möchte, kann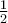 aber auch lang als $$\frac{1}{2}$$ schreiben.
aber auch lang als $$\frac{1}{2}$$ schreiben.Ausnahme 2
Wenn Parameter ebenfalls TeX-Befehle sind, benötigen sie keine geschweiften KlammernEbenfalls können (≠ müssen) die geschweiften Klammern weggelassen werden, wenn der Parameter wiederum aus einem Befehl besteht:
Beispiel 1:
$$ x_\text{max} $$wird zuBeispiel 2:
$$ x^\gamma $$ wird zuDie Befehle "Tief-" bzw. "Hochstellung" (_, ^) haben als Parameter einen weiteren Befehl (hier:\textbzw. \gamma). Diese Parameter müssen nicht zwingend in geschweifte Klammern gesetzt werden, der Parameter eines verschachtelten Befehls (hier: max) aber schon. Die verschachtelten Varianten,$$ x_{\text{max}} $$bzw. $$ x^{\gamma} $$, funktionieren aber trotzdem: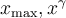
Ausnahme 3
Spezialfälle mit eckigen KlammernEine weitere Ausnahme von den drei Grundregeln bilden die sehr seltenen (!) von eckigen Klammern (also: [ und ] ) eingeschlossenen Parameter. Eine Umsetzung mit geschweiften Klammern führt zu fehlerhafter Darstellung:
Beispiel für eckige Klammern bei \xrightarrow:
$$ A \xrightarrow[\text{unten}]{\text{oben}} B $$führt zu
-
-
Bevor man sich an die Eingabe spezieller und komplexer Formeln macht, sollte man hier kurz die Grundlagen zur Zeichendarstellung (Buchstaben und Zahlen, um Schriftarten, Größenverhältnisse, Umlaute, etc.) überfliegen, um sich mit der Darstellung von
- Zahlen, z.B.:
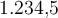
- Buchstaben, z.B.:
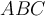
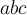
- Akzenten und Diakritika, z.B.:
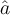
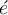
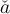
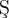
- Schriftarten, z.B.:
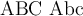
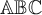
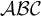
- und Formelkürzeln, z.B.:
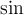
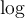
vertraut zu machen:
-
2.1 Darstellung von Zahlen
Bei der Benutzung von Zahlen innerhalb der Doppel-$-Bereiche ist nicht viel zu beachten. Alle Zahlen können in TeX dargestellt werden. Wenn ein Komma als Dezimaltrennzeichen benutzt wird, kommt es beim Moodle-TeX-Fitler zu leichten Verzerrungen im Zeichenabstand, wie in anderen TeX-Filtern auch :-( (s. z.B. hier).
Zahlen:
$$1234567890$$führt zu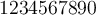
Kommata sollten in
{}gesetzt werden:
$$ 1{,}23 $$führt zu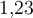
Punkte als Tausender-Trennzeichen können ohne
{}genutzt werden:
$$ 1.234.567.890{,}00 $$führt zu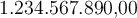
-
2.2 Text, Akzente, Diakritika, Streichungen
Ebenso einfach wie die Nutzung von Zahlen ist die Benutzung von Buchstaben. Für Formelteile, einzelne Worte und Wortteile können Sie die Buchstaben einfach innerhalb der $-Symbole platzieren.
Die Nutzung von Umlauten ist abhängig von der gewählten Schriftart (s. Abschnitt "Schriftarten"). Ohne Angabe einer speziellen Schriftart oder dem Befeht \text werden ausschließlich Groß- und Kleinbuchstaben unterstützt:
Buchstaben exkl. Umlaute:
$$ ABCDabcd $$führt zuBeliebter Fehler: Umlaute ohne definierte Schriftart
Für Umlaute muss eine entsprechende Schriftart oder mind. der Befehl \text{...} (s. Abschnitt "Schriftarten") gewählt werden!
Ein Workaround ist die Funktion \ddot, so führt $$\ddot{a}$$ zu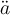 .
.Akzente und buchstabenspezifische Sonderzeichen
Sie können Akzente über spezielle Befehle generieren, die mit einem Backslash eingeläutet werden. Die wichtigsten finden Sie in dieser Liste:* Tipp: Für das arithmetische Mittel verwenden Sie besser die Funktion
$$ \overline{x} $$(s. u.)
Mathematische "Akzente":
Neben dem oben erwähntem Punkt \dot (
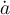 ), dem Trema/Doppelpunkt \ddot (
), dem Trema/Doppelpunkt \ddot (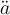 ), der Tilde \tilde (
), der Tilde \tilde (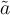 ) und dem Zirkumflex/Dach \hat (
) und dem Zirkumflex/Dach \hat (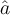 ) gibt es weitere in der mathematischen Darstellung relevante Akzente:
) gibt es weitere in der mathematischen Darstellung relevante Akzente:Name TeX-Befehl Ergebnis "x quer", Mittelwert $$\overline x$$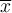
"unterstrichen" $$\underline a$$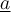
"doppelt unterstrichen" $$\underline{\underline a}$$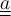
Vektorpfeil $$\vec a$$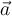 *
** Tipp: Für mehr als ein Zeichen besser $$ \overrightarrow $$ (s. Abschnitt "Pfeile und Linien") benutzen!
Streichungen
Streichung Syntax Egrgebnis durchgestrichen $$ a\!\!\!/$$,$$ y\!\!\!/$$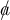 ,
,
Negationen $$ \not< $$,$$ \not\subset $$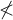 ,
,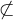
-
2.3 Schriftarten
Am einfachsten ist es, einfach Text innerhalb des TeX-Strings einzugeben oder den Befehl \text zu nutzen. Je nach Nutzung werden Buchstaben in verschiedenen Schriftarten gerendert. Den Unterschied zwischen einer "unformatierten" Verwendung von Zeichen wie
und dem Befehl \text
besteht a) in der Unterstützung von Umlauten innerhalb von \text und b) der Verwendung einer anderen Schriftart: Ohne \text wird "MathNormal" (kursiv), innerhalb von \text wird "MathRoman" (aufrecht, s.u.) verwendet.
Verfügbare Schriftarten (alphabetisch)
"Boldsymbol":
$$\boldsymbol{123ABCabc}$$ führt zuBoldsymbol ist eine kursive Fettschrift, unterstützt Zahlen, Groß- und Kleinbuchstaben ohne Umlaute.
"MathBB":
$$\mathbb{ABCDEF}$$führt zuMathBB ist eine Sonderschrift mit doppelten Vertikalen, unterstützt ausschließlich Großbuchstaben, keine Umlaute, keine Kleinbuchstaben, keine Zahlen. Sie wird vor allem zur Darstellung mathematischer Mengen (Natürliche Zahlen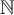 oder Ganzzahlen
oder Ganzzahlen 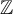 ) genutzt.
) genutzt.
"MathBoldFace": $$\mathbf{123ABCabc}$$ führt zu
MathBoldFace ist eine aufrechte Fettschrift. Unterstützt werden Zahlen, Groß- und Kleinbuchstaben ohne Umlaute.
"MathCalligraph":
$$\mathcal{ABCDEF}$$führt zuMathCalligraph ist eine Kalligraphieschrift, unterstützt ausschließlich Großbuchstaben ohne Umlaute.
"MathFraktur":
$$\mathfrak{123ABCDEFabcdef}$$ führt zuMathFraktur bietet Frakturbuchstaben, unterstützt Zahlen, Groß- und Kleinbuchstaben ohne Umlaute. Sie werden z.B. in der Mathematik als (veraltete?) Typographie für Vektoren, Matrizen und Tensoren sowie für den Real- und Imaginärteil (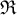 bzw.
bzw. 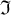 ) einer komplexen Zahl genutzt. Für die letzten beiden Beispiele kann man mit auch die Kurzformen
) einer komplexen Zahl genutzt. Für die letzten beiden Beispiele kann man mit auch die Kurzformen $$\Re$$(=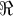 ) und
) und $$\Im$$(=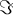 ) nutzen. Vereinzelt für hyperbolische trigonometrische
Funktionen (Mathematik) oder vektorielle und tensorielle Größen (Physik) verwendet. Weiterer Einsatzbereich sind Ideale/Idealoperatoren in der Mathematik.
) nutzen. Vereinzelt für hyperbolische trigonometrische
Funktionen (Mathematik) oder vektorielle und tensorielle Größen (Physik) verwendet. Weiterer Einsatzbereich sind Ideale/Idealoperatoren in der Mathematik.
"MathNormal":
$$\mathnormal{123ABCabc}$$ führt zuMathNormal ist eine kursive Serifenschrift, unterstützt Zahlen, Groß- und Kleinbuchstaben ohne Umlaute, wird normalerweise für Variablen (z.B. x, a, n, etc.) benutzt. "MathNormal" ist aber auch die Standardschrift, auf den Befehl \mathnormal kann also meistens verzichtet werden.
"MathRoman":
$$\mathrm{123ABCabc}$$ führt zuMathRoman ist eine aufrechte Serifenschrift, unterstützt Zahlen, Groß- und Kleinbuchstaben ohne Umlaute, wird normalerweise für Funktionen (z.B. cos, log, etc.) benutzt. MathRoman wird auch via \text gesetzt und unterstützt dann auch Umlaute.
"MathSansSerif":
$$\mathsf{123ABCabc}$$ führt zuMathSansSerif ist eine aufrechte serifenlose Schrift, unterstützt Zahlen, Groß- und Kleinbuchstaben ohne Umlaute. -
2.4 "Klammerpflicht" bei längeren Parametern
Die Größenverhältnisse verschiedener Textteile können Sie mit dem Befehl
$$ \text{...} $$sicherstellen. Wenn Sie größere Zeichenketten (also mehr als ein einzelnes Zeichen) z.B. hoch- oder tiefstellen wollen, können Sie wie im unten stehenden Beispiel für Zeichen der Formel (hier: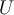 bzw.
bzw. 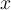 ) einfach die entsprechenden Buchstaben verwenden, für die hoch- oder tiefgestellten Bereiche müssen Sie die Befehle ^ (für
hochgestellt) bzw.
_ (für tiefgestellt) und den Befehl \text{...} benutzen.
) einfach die entsprechenden Buchstaben verwenden, für die hoch- oder tiefgestellten Bereiche müssen Sie die Befehle ^ (für
hochgestellt) bzw.
_ (für tiefgestellt) und den Befehl \text{...} benutzen.Beispiele:
$$ U_\text{Gesamt} $$führt zu
$$ x^\text{Stichprobe} $$führt zu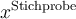
Beliebter Fehler: Nur das erste Zeichen wird hoch-/tiefgestellt
Wenn Sie den zusammengehörigen Teil der Hoch- bzw. Tiefstellung nicht als Parameter in geschweiften Klammern des Befehls \text definieren, gelten die Positionsangaben ^ bzw. _ nur für das jeweils erste Zeichen der folgenden Zeichenkette!Gleiches gilt für alle Parameter, die aus mehr als einem Zeichen bestehen, z.B.
-
2.5 Mathematische Funktionsnamen
Es stehen bereits vorgefertigte Textbefehle wie z.B. die Sinus-Angabe in
$$ \sin(x) $$(wird zu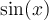 ) zur Verfügung. Sollte ein benötigter Ausdruck nicht in der folgenden Tabelle vorhanden sein, können Sie diesen über
) zur Verfügung. Sollte ein benötigter Ausdruck nicht in der folgenden Tabelle vorhanden sein, können Sie diesen über $$ \text{benötigteFormel} $$(wird zu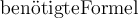 ) erzeugen. Die Schriftart ist in beiden Fällen "MathRoman".
) erzeugen. Die Schriftart ist in beiden Fällen "MathRoman".Zur Verfügung stehen (in alphabetischer Reihenfolge):
-
2.6 Weitere Sonderzeichen
Eine Liste weiterer Sonderzeichen (ohne Anspruch auf Vollständigkeit) finden Sie hier. Bitte beachten Sie, dass Sie mathematische Operatoren und Relationszechen im Abschnitt Operatoren und Relationen finden.
- Zahlen, z.B.:
-
-
3.1 Liste griechischer Buchstaben
Für alle griechischen Kleinbuchstaben existieren TeX-Befehle. Für manche Kleinbuchstaben gibt es mehrere Darstellungen. Sofern als TeX-Befehl verfügbar, funktionieren diese meist mit dem Zusatz var (für Variation), also z.B. \pi oder \varpi. Für manche Großbuchstaben existieren keine TeX-Befehle. In diesen (mit * gekennzeichneten) Fällen kann \mathrm in Kombination mit einem entsprechenden lateinischen Buchstaben verwendet werden:
-
3.2 Griechische Buchstaben und Schriftarten
Da es bei Großbuchstaben zu Problemen in der Darstellung kommen kann, sollte auf die Formatierung griechischer Buchstaben in besonderen Schriftarten grds. verzichtet werden.Die Kleinbuchstaben des griechischen Alphabets werden prinzipiell in allen Schriftarten unterstützt, wenn auch die Formatierung (z.B. als Frakturschrift) meist nicht sichtbar wird:
-
-
-
4.1 Klammern und Begrenzungssymbole allgemein
Runde Klammern können einfach über die Tastatur eingegeben werden,
$$f(x)$$ führt also zu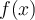
Eckige Klammern werden ebenfalls einfach eingegeben,
$$[A]$$ ergibt![[A] [A]](https://moodle.thga.de/filter/tex/pix.php/7e2bf8880d46cb84f91d8740b2659a88.png)
Alternativ funktinieren die Befehle $$\lbrack ... \rbrack$$:

Geschweifte Klammern können über die Tastatur eingegeben werden, müssen aber mit \ eingeleitet werden:
$$\{...\}$$ führt zu
Alternativ funktinieren die Befehle $$\lbrace ... \rbrace$$:

Spitze Klammern werden mit
$$\langle ... \rangle$$ generiert:
Nicht empfohlen ist die Tastatureingabe von $$ < ... > $$, diese sind eher für Grüßenverhältnisse ('größer als', 'kleiner als') zu nutzen:

Rundungsklammern: Für Auf- und Abrundungsfunktionen steht
$$\lceil x \rceil$$ bzw. $$\lfloor x \rfloor$$ zur Verfügung: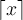 bzw.
bzw. 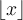
Betragsstriche erstellt man am einfachsten mit $$|-2|$$:
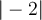
Alternativ stehen die Befehle $$\vert -2 \vert$$ und $$\left|-2\right|$$ zur Verfügung:
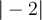 ,
, 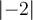
Normstriche benötigen einen zusätzlichen \, also z.B. $$\|-2\|$$:
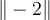
Alternativ stehen die Befehle $$\Vert -2 \Vert$$ zur Verfügung:
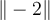 Grundsätzlich ist bei TeX-Befehlen auf Groß- und Kleinschreibung zu achten, hier an \vert und \Vert gut sichtbar. Das gilt aber auch für z.B. \gamma und \Gamma (s. "Liste griechische Buchstaben") oder \bigl und \Bigl (s. "Größenvariable Symbole").
Grundsätzlich ist bei TeX-Befehlen auf Groß- und Kleinschreibung zu achten, hier an \vert und \Vert gut sichtbar. Das gilt aber auch für z.B. \gamma und \Gamma (s. "Liste griechische Buchstaben") oder \bigl und \Bigl (s. "Größenvariable Symbole"). -
4.2 Größenvariable Symbole (autom. Anpassung)
Wenn man einen "hohen" Formelbestandteil, z.B. einen Doppelbruch, mit Begrenzungssymbolen versehen möchte, führen die oben beschriebenen Befehle zu einer nur überschaubar ansehnlichen Darstellung. Beispielhaft sei hier ein (ebenfalls via \dfac statt \frac größenangepasster) Doppelbruch eingeklammert,
$$(\dfrac{\dfrac 1x}{\dfrac{y}{263}})$$:Diese viel zu kleinen Klammern kann man mittels \left( und \right) anpassen,
$$\left( \dfrac{\dfrac 1x}{\dfrac{y}{263}} \right)$$ führt zuDie Zusätze \left und \right funktionieren auch mit allen anderen Klammer- und Begrenzungssymbolen:
Eckige Klammern:
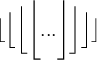
$$\left[ ... \right]$$ führt zu![\left[ \dfrac{\dfrac 1x}{\dfrac{y}{263}} \right] \left[ \dfrac{\dfrac 1x}{\dfrac{y}{263}} \right]](https://moodle.thga.de/filter/tex/pix.php/ae19a076e3976fc2d54ec0fb885ec0f4.png)
Alternative $$\left\lbrack ... \right\rbrack$$ führt zu
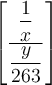
Geschweifte Klammern:
$$\left\{ ... \right\}$$ führt zu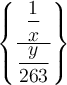
Alternative $$\left\lbrace ... \right\rbrace$$ führt zu
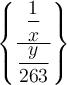
Spitze Klammern:
$$\left\langle ... \right\rangle$$ führt zu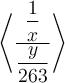
-
4.3 Größenvariable Symbole (manuelle Anpassung)
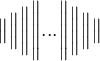
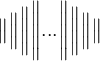
Klammern können auch manuell in der Höhe angepasst werden. Über eine vierstufige Größenangabe (big, Big, bigg, Bigg) und eine Richtungsangabe (l, r) können die Höhen der Zeichen angegeben werden. Beispiele für runde Klammern:
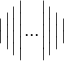
$$\bigl( ... \bigr)$$führt zu ,
,$$\Bigl( ... \Bigr)$$führt zu ,
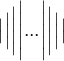
,$$\biggl( ... \biggr)$$führt zu , und
, und$$\Biggl( ... \Biggr)$$führt zu .
.
Runde Klammern:
$$\bigl( \Bigl( \biggl( \Biggl( ... \Biggr) \biggr) \Bigr) \bigr)$$
Eckige Klammern:
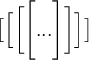
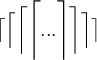
$$\bigl[ \Bigl[ \biggl[ \Biggl[ ... \Biggr] \biggr] \Bigr] \bigr] $$Alternative
$$\bigl\lbrack \Bigl\lbrack \biggl\lbrack \Biggl\lbrack ... \Biggr\rbrack \biggr\rbrack \Bigr\rbrack \bigr\rbrack $$
Geschweifte Klammern:
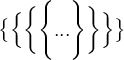
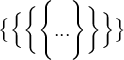
$$\bigl\{ \Bigl\{ \biggl\{ \Biggl\{ ... \Biggr\} \biggr\} \Bigr\} \bigr\}$$Alternative
$$ \bigl\lbrace \Bigl\lbrace \biggl\lbrace \Biggl\lbrace ... \Biggr\rbrace \biggr\rbrace \Bigr\rbrace \bigr\rbrace $$
Spitze Klammern:
$$\bigl\langle \Bigl\langle \biggl\langle \Biggl\langle ... \Biggr\rangle \biggr\rangle \Bigr\rangle \bigr\rangle $$
Rundungsklammern:
$$\bigl\lceil \Bigl\lceil \biggl\lceil \Biggl\lceil ... \Biggr\rceil \biggr\rceil \Bigr\rceil \bigr\rceil $$$$\bigl\lfloor \Bigl\lfloor \biggl\lfloor \Biggl\lfloor ... \Biggr\rfloor \biggr\rfloor \Bigr\rfloor \bigr\rfloor $$
Betragsstriche:
$$\bigl| \Bigl| \biggl| \Biggl| ... \Biggr| \biggr| \Bigr| \bigr|$$Alternative
$$ \bigl\vert \Bigl\vert \biggl\vert \Biggl\vert ... \Biggr\vert \biggr\vert \Bigr\vert \bigr\vert $$
Normstriche:
$$\bigl\| \Bigl\| \biggl\| \Biggl\| ... \Biggr\| \biggr\| \Bigr\| \bigr\|$$Alternative
$$ \bigl\Vert \Bigl\Vert \biggl\Vert \Biggl\Vert ... \Biggr\Vert \biggr\Vert \Bigr\Vert \bigr\Vert $$ -
4.4 Klammer-Sonderformen, einseitige Begrenzer
Mit \lgroup und \rgroup stehen "gerade Klammern" zur Verfügung: Der Vergleich von
$$\left\lgroup a \right\rgroup $$ und $$\left( a \right) $$ zeigt die unterschiedliche Darstellung:Einsatzzenarien können mehrzeilige Darstellungen (z.B. Matritzen, mehr unter Zeichen und Formeln) sein:
$$\left\lgroup \begin{matrix} x & y \\ z & v \end{matrix} \right\rgroup$$
Für einseitige Klammern kann ein Punkt als "Platzhalter" genutzt werden: Ein \left. oder \right. führt zur Auslassung des entsprechenden Klammerzeichens:
$$\left( x \right. $$ bzw. $$\left. x \right) $$ führen zuDie Platzhalter funktionieren auch mit den eckigen, geschweiften, spitzen und Rundungsklammern sowie Betrags- und Normstrichen:
Einsatzbeispiel für einseitige Abgrenzer:
$$\left. \dfrac AB \right\} \to X $$ führt zu
Eine weitere Variante einseitiger Begrenzungssymbole (links) sind Fallunterscheidungen via \begin{cases} und \end{cases}:
$$ \begin{cases} x \end{cases} $$ führt zuEinsatzbeispiel für eine Fallunterscheidung:
$$ f(n) =\begin{cases}
n/2, & \text{wenn }n\text{ gerade,} \\
3n+1, & \text{wenn }n\text{ ungerade.}
\end{cases} $$
Ecken können mittels \ulcorner, \urcorner, \llcorner und \lrcorner (u/l = upper/lower + l/r = left/right + corner) generiert werden:
$$\ulcorner A $$,
$$ A \urcorner $$,
$$\llcorner A $$ und
$$\lrcorner A $$ führen zuEine Kombination von je einer linken und rechten Variante ist möglich:
$$\ulcorner A \urcorner $$ führt zu
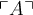 ,
,$$\llcorner A \lrcorner $$ führt zu
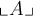 .
.
Mit \lmoustache und \rmoustache steht ein weiterer Exot zur Verfügung:
$$\lmoustache \mathbb{Q}(t)\rmoustache$$ führt zu
-
-
-
5.1 Pfeile und Linien über und unter einem Term
Für z.B. Vektoren, Strecken oder Schachtelungen stehen verschiedene Befehle für Linien, Pfeile und Klammern zur Verfügung:
Ober- und Unterstriche:
$$\overline A $$ führt zu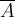 ,
,$$\overline {ABC} $$ führt zu
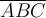 ,
,$$\underline {ABC} $$ führt zu
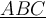 .Wenn der Ober- oder Unterstrich über mehrere Zeichen gehen soll, müssen diese in geschweiften Klammern gruppiert werden.
.Wenn der Ober- oder Unterstrich über mehrere Zeichen gehen soll, müssen diese in geschweiften Klammern gruppiert werden.
Vektorpfeile:
$$\overrightarrow A $$ führt zu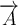
$$\overrightarrow {ABC} $$ führt zu
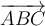
$$\overleftarrow A $$ führt zu
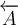
$$\overleftarrow {ABC} $$ führt zu
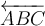
Dächer:
Während \hat für einzelne Zeichen ausreicht, z.B. in $$\hat A$$ =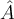 , muss für "große Dächer" über mehrere Zeichen der der Befeht \widehat genutzt werden:
, muss für "große Dächer" über mehrere Zeichen der der Befeht \widehat genutzt werden:
Klammern über und unter einem Term:
$$ \overbrace {ABC} $$ =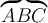
-
5.2 Einfachpfeile
-
5.4 Doppelte Pfeile und Doppelspitzen
-
-
-
6.1 Addition, Subtraktion, Multiplikation,Division
-
6.2 Vereinigung, Durchschnitt, Und-Oder-Junktoren
-
6.3 Ordnungsrelationen
-
6.4 Negierte Ordnungsrelationen
-
6.5 Äquivalenzrelationen
-
6.7 Sonstige Operatoren und Relationen
-
-
-
7.1 Hoch- und Tiefstellung
-
7.2 Brüche
-
7.3 Matrizen
Matritzen sin eine erwähnenswerte Ausnahme von der bisherigen TeX-Logik, da sie in speziellen - mit\begineingeleiteten und mit\endbeendeten - Umgebungen notiert werden. Wie auch in den weiter unten folgenden Beispielen zu mehrzeiligen Gleichungen werden die einzelnen Zeilen mit einemm Doppel-Backslash \\ voneinander getrennt. Die Elemente je Zeile werden mit einem & getrennt.
Beispiel:
$$ \begin{pmatrix} x & y \\ z & v \end{pmatrix} $$führt zuFür größere Felder kann es sich anbieten, den TeX-Code in mehreren Zeilen zu notieren (was wiederum höhere Übersichtlichkeit, aber evtl. andere Probleme mit sich bringt. Siehe dazu den Abschnitt "Tipps, Tricks, Troubleshooting"):
$$ \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix} $$
Matrizen ohne Klammern:$$ \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} $$führt zu
Kleine Matrizen ohne Klammern:
$$ \begin{smallmatrix} a & b \\ c & d \end{smallmatrix} $$führt zu
Matrizen mit runden Klammern:
$$ \begin{pmatrix} x & y \\ z & v \end{pmatrix} $$führt zu
Matrizen mit eckigen Klammern:
$$ \begin{bmatrix} 1 & 2 \\ 3& 4 \end{bmatrix} $$führt zu
Matrizen mit geschweiften Klammern:
$$ \begin{Bmatrix} x & y \\ z & v \end{Bmatrix} $$führt zu
Matrizen mit (Betrags-) Strichen:
$$ \begin{vmatrix} x & y \\ z & v \end{vmatrix} $$führt zu
Matrizen mit (doppeltn, Norm-) Strichen:
$$ \begin{Vmatrix} x & y \\ z & v \end{Vmatrix} $$führt zu
Sonderfälle und besondere Darstellungen:
Eine Matrix mit abgetrennten Bereichen oder Blöcken kann man auf verschiedene Weise generieren, z.B.
Eine Matrix mit Punkten als Platzhalter für Reihen kann man mit \cdots, \ddots und \vdots (für horizontale, diagonale und vertikale Punkte) generieren, z.B.
-
7.4 Mathematische Formelzeichen
-
-
Wenn man mit den obigen Erläuterungen alle benötigten Zeichen darstellen kann, können diese zu komplexen Formeln zusammengesetzt werden. Um diese Formeln zu "setzen", stehen verschiedene Formatierungsmöglichkeiten zur Verfügung:
-
8.1 Leerzeichen
Um Leerzeichen, welche in TeX normalerweise ignoriert werden, zu erzwingen, stehen fünf vergrößerte Zeichenabstände (und ein verringerter Zeichenabstand) zur Verfügung.
Damit kann man in einer Zeile bestimmte Teile innerhalb einer TeX-Notation abrücken:
Beispiel 1 Syntax: Für den freien Fall einer Masse
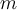 sei das Weg-Zeit-Gesetz
sei das Weg-Zeit-Gesetz$$s=s(t)=s_0-\frac 12 \cdot t^2\qquad mit \qquad s_0=125 \qquad und \qquad g=10$$.Mit den verschiedenen Abständen kann man auch Formeln nummerieren, allerdings ist z.B. die Rechtsbündigkeit der Formelnummerierung im folgenden Beispiel eher "Versuch und Irrtum", da hier z.B: $$\quads$$ mit $$\ $$ kombiniert werden müssen, bis die Abstände stimmen.
Besser geht das in den align- bzw. alignat-Umgebungen, die in den nächsten Abschnitten 8.2 und 8.3 erläutert werden.Beispiel 2 (Formelnummerierung): Syntax: Für die Potentialdifferenz zwischen dem Punkt P (in der Niveaufläche mit dem Potential WP gelegen) und dem Punkt P0 auf dem Geoid (in der als Nullniveau definierten Potentialfläche W0 gelegen) erhält man analog
also
oder
$$ - \int\limits_{P_0}^{P} dW = \int\limits_0^P g \cdot dh \qquad\qquad\qquad(1.1-1)$$
also$$ W_0 - W_P = g_m \cdot H_P = C_P \qquad \ (1.1-2)$$
oder$$ H_P = \dfrac {W_0 - W_P} {g_{\tilde{m}}} \qquad\qquad\qquad \ \ (1.1-3)$$Um ein Gefühl für die einzelnen Abstände zu bekommen, hier eine kleine Hilfestellung:
-
8.2 Ausrichtung mehrzeiliger Gleichungen
Wenn man Rechenschritte oder mehrteilige Gleichungen abbilden möchte, sollten die Gleichheitszeichen der einzelnen Zeilen um der Konvention und der Übersichtlichkeit Willen untereinander stehen.
- Die entsprechenden Einrückungen erreicht man über einen {align}-Bereich, der mit \begin{align} eingeleitet und mit \end{align} beendet wird.
- Jede Zeile innerhalb der align-Umgebung wird mit einem Doppelbackslash (\\) beendet. Die letzte Zeile benötigt kein Endsymbol.
- Die Stellen der Gleichung, welche jeweils aneinander ausgerichtet sein sollen, kennzeichnet man mit einem &-Symbol.
- Die Zeilennummerierung wird automatisch hinzugefügt, können aber unterdrückt werden.
Im ersten Beispiel wird die linke Seite der Gleichung ab Zeile 2 nicht wiederholt, jede Zeile startet also sofort mit dem &=, so dass die Gleichheitszeichen untereinander stehen, links vom Gleichheitszeichen ab der zweiten Zeile aber "nichts" dargestellt wird.
Gleichheitszeichen untereinander, links "leer": Syntax 
$$ \begin{align}
a&=b+c\\
&=5+7\\
&=12
\end{align} $$Im zweiten Beispiel sieht man, dass Teile der Formel links von der &-Markierung rechtsbündig und rechts von der &-Markierung linksbündig dargestellt werden.
Gleichheitszeichen untereinander: Syntax 
$$\begin{align}
1.234^2&=1.522.756\\
123^2&=15.129\\
12^2&=144\\
9^2&=81
\end{align}$$Das dritte Beispiel zeigt, dass nicht nur Gleichheitszeichen, sondern auch andere Zeichen jeder Zeile mittels & aneinander ausgerichtet werden können.
Rechenzeichen untereinander: Syntax 
$$ \begin{align}
a*b&+x\\
c&+x\\
(a+c)^2*b&+x
\end{align} $$Zeilennummerierung unterdrücken
Um die automatische Zeilennummerierung zu unterdrücken, kann {align*} benutzt werden:
Zeilennummerierung unterdrückt: Syntax 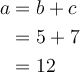
$$ \begin{align*}
a&=b+c\\
&=5+7\\
&=12
\end{align*} $$Ausnahmen in der Zeilennummerierung
Um einzelne Zeilennummern zu unterdrücken, können innerhalb von der {align}-Umgebung (mit automatischer Nummerierung) einzelne Zeilen vor dem beendenden \\ mit dem Befehl \notag versehen werden. Diese Zeilen werden in der Nummerierung übersprungen. Ab der nächsten Zeile wird weitergezählt.
Gleichheitszeichen untereinander, einzelne Zeilennummerierungen unterdrücken: Syntax 
$$ \begin{align}
a&=b+c\\
&=5+7\notag\\
&=12
\end{align} $$Analog können in der {align*}-Umgebung (ohne automatische Nummerierung) einzelne Zeilen gekennzeichnet werden, indem ans Zeilenende vor den \\ ein \tag{...} angegeben wird. So können z.B. wichtige Zwischenergebnisse gekennzeichnet werden, auf die z.B. im Text weiter eingegangen wird.
Gleichheitszeichen untereinander, einzelne Zeilennummerierungen erzwingen: Syntax 
$$ \begin{align*}
a&=b+c\\
&=5+7\tag{q.e.d.}\\
&=12
\end{align*} $$ -
8.3 Mehrzeilige Gleichungen (für Fortgeschrittene)
Die {align}-Umgebung kann mehrere Zeichen nur an einer Stelle aneinander ausrichten. Sollen mehrere Blöcke ausgerichtet werden, muss die {alignat}-Umgebung genutzt werden. In einem weiteren Parameter wird angegeben, wieviele Teile jede Zeile besitzen soll.
Im ersten Beispiel wird also über \begin{alignat} der Bereich eingeleitet und über die folgende {3} angegeben, dass jede Zeile drei Teile besitzt: Der erste reicht bis zum Gleichheitszeichen (&=), der zweite bis vor das erzwungene großen Leerzeichen (&\qquad). Die zweite und die dritte Zeile wird über die jew. &s an der oberen Zeile ausgerichtet und benötigt die Angabe des \qquad nicht mehr zwingend.
Im zweiten Beispiel sehen Sie, wie über ein weiteres &-Zeichen die Ausrichtung (Rechts- und Linksbündigkeit) der einzelnen Formelteile manipuliert werden kann:
Zeilennummerierung unterdrücken, mehrere Blöcke ausrichten
Auch in der {alignat}-Umgebung kann mit einem * die Zeilennummerierung unterdrückt werden: Innerhalb von {alignat} werden mit \notag versehene Zeilen nicht nummeriert bzw. können innerhalb von {alignat*} mit \tag{...} zusätzliche Kennzeichnungen hinzugefügt werden.
Ein letztes Beispiel - nun mit vier Abschnitten (also {alignat*}{4}) - soll verdeutlichen, wie ein Teil einer Zeile ausgelassen werden kann, wenn z.B. die verschiedenen Zeilen unterschiedlich viele Rechenschritte beinhalten. Die Positionierung der &-Zeichen beeinflusst, ob und welche Ausrihtungszeichen (hier: Gleichheitszeichen) angezeigt werden:
-
8.4 Tabellen
Um eine Tabelle in TeX zu erstellen, kann die {array}-Umgebung genutzt werden.
- Nach dem einleitenden \begin{array} wird in geschweiften Klammern definiert, wie die Spalten voneinander abgetrennt sein sollen. {|c||c|c|c|} erzeugt dabei vier Spalten, wobei die erste rechts durch eine doppelte Linie || begrenzt wird.
- Die Zelleninhalte einer Zeile werden hintereinander weg notiert, wobei die Zellen jeweils mit einem &-Zeichen getrennt werden.
- Horizontale Linien können mit dem Befehl \hline zwischen den jeweiligen Zeilen platziert werden.
- Das Ganze muss über ein \end{array} geschlossen werden:
Da die erste Zelle der Kopfzeile leer ist, beginnt die erste Zeile direkt mit einem & und dann mit dem Inhalt der zweiten Zelle:
Syntax Ergebnis $$ \begin{array}{|c||c|c|c|}
& \text{Spalte1} & \text{Spalte2} & \text{Spalte3}\\
\hline
\text{Zeile1} & 1 & 2 & 3\\
\text{Zeile2} & 1 & 2 & 3\\
\text{Zeile3} & 1 & 2 & 3\\
\end{array} $$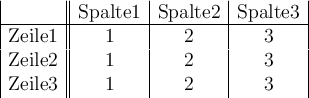
-
-
-
Mehrzeilige Eingabe der TeX-Notation
Die Eingabe von TeX-Notation in mehreren Zeilen kann manchmal zu Problemen führen. Prinzipiell ist eine Eingabe in mehreren Zeilen möglich:
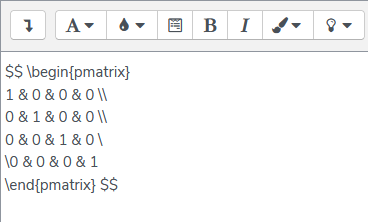
Sogar eine HTML-Formatierung incl. Sonderzeichen (&) und Absätzen (<p>...</p>) kann den TeX-Filter nicht stoppen:
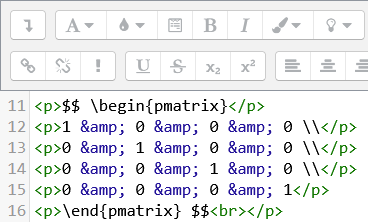
Allerdings kann es vorkommen, dass sich durch häufiges Umbrechen und Umformatieren weitere HTML-Auszeichnungen in die TeX-Notation mischen, die den Filter bei der Übersetzung des $$ ... $$-Inhalts in die entspr. Formel scheitern lassen.
Achten Sie also bitte auf eine möglichst "störungsfreie" Codierung Ihrer TeX-Eingabe. -
HTML-Artefakte
In der gleichen Liga spielen Überreste von z.B. einem Versuch, Teile einer Formel einzufärben: Wenn man innerhalb der TeX-Notation mit Schrift- und Hintergrundfarbe experimentiert, werden entspr. HTML-Codes in die TeX-Notation geschrieben. Das Wort Test ist in diesem Beispiel farbig hervorgehoben. Im HTML-Quellcode, der vom Editor generiert wird, steht allerdings
<span style="background-color: rgb(227, 204, 206); color: rgb(153, 0, 10);">Test</span>. Wenn das innerhalb einer TeX-Notation passiert, also statt $$ \frac{2}{3} $$ dort $$ \frac{<span style="background-color: red"><2</span>}{3} $$ steht, kommt das heraus:Versetzen Sie den Editor in den HTML-Modus (Button "</>" in der zweiten Editorzeile) und bereinigen Sie das HTML innerhalb der $$...$$ von nicht benötigten Zeichen. -
Kollision mit dem Emoticon-Filter
Moodle verfügt über einen Emoticon-Filter, der automatisch Zeichenfolgen wie :) in Grafiken, hier
übersetzt. Dabei werden im Hintergrund Quelltexte nach solchen Zeichenfolgen durchsucht und automatisch statt den charakteristischen Zeichenfolgen ein Bild eingebunden.
Nun gibt es gewisse "Überschneidungen" zwischen Emoticons und Mathematik - z.B. sind Doppelpunkt und Klammer :( oder (n) in Formeln durchaus denkbar, diese beiden Zeichenketten führen aber z.B. zu
bzw.
.
Auch hier reagiert der TeX-Filter allergisch auf die eingebetteten Emoticon-Grafiken, daher sollten Sie in den Filter-Einstellungen Ihrer Kurse, in denen TeX-Formeln zum EInsatz kommen, den Emoticon-Filter deaktivieren. Standardmäßig ist in unseren Moodle-Kursen "Emoticon als Bild zeigen" aus-, "TeX-Notation" angeschaltet. -
Debugging
Korrekt gerenderte TeX-Grafiken wie auch fehlerhafte Notationen sind anklickbar und zeigen dann den TeX Quellcode in einem Extrafenster:
Fehlerhafte Notation, ebenfalls anklickbar:
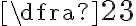 Untersuchen Sie die Notation auf entspr. Fehler:
Untersuchen Sie die Notation auf entspr. Fehler:- Schreibfehler in den Befehlen, z.B. \dfarc statt \dfrac
- Nicht geschlossene Parameter-Klammern
- Verirrungen bei verschachtelten Parametern: Achten Sie darauf, dass alle Klammern auch wieder geschlossen werden.
- Verzichten Sie auf Farben und sonstige Beeinflussung der Darstellung (Textgröße, Textausrichtung, Schriftart - jenseits der TeX-Schriftarten, usw.)
-
Reichen Sonderzeichen oder Gleichungseditor?
Wenn Sie die Länge der obigen TeX-Ausführungen und die Komplexität der Notation eher abschreckt und Sie nur ab und zu ein Summenzeichen oder eine Zahl hochstellen möchten, reichen die Standardfunktionen des Editors.x2 oder NH3 kann man mittels Hoch- und Tiefstellung, Σ, Ω, ≠ und viele mehr mittels "Sonderzeichen einfügen" erzeugen. Diese Funktionen finden Sie in der zweiten Buttonzeile des Moodle-Standardeditors (ausklappen mit ↴).
Dort finden Sie auch den Button "Gleichungseditor", der Ihnen einen (rudimentären!) Formeleditor zur Verfügung stellt. Dabei handelt es sich um eine grafische Oberfläche, die ausgewählte TeX-Befehle vorhält, die man mit Maus und Tastatur einfügen und bearbeiten kann.
-
-
Dieser Online-Kurs "Formeln mit TeX in Moodle" von Martin Smaxwil ist lizenziert unter einer Creative Commons Namensnennung - Weitergabe unter gleichen Bedingungen 4.0 International Lizenz. Er enthält Teile aus dem Wikipedia-Inhalt http://de.wikipedia.org/wiki/Hilfe:TeX (Stand: 30.03.2022). Die Liste der am Original beteiligten Autoren finden Sie hier. Weitere Infos finden Sie unter https://moodle.thga.de/cc-lizenzen.


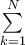
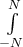
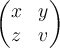

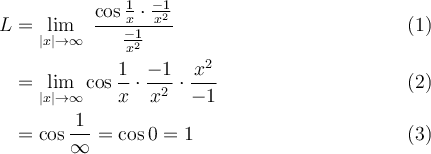
![\phi_n(\kappa) = \frac{1}{4\pi^2\kappa^2} \int\limits_0^\infty \frac{\sin(\kappa R)}{\kappa R} \frac{\partial}{\partial R} \left[ R^2 \frac{\partial D_n(R)}{\partial R} \right]\mathrm dR \phi_n(\kappa) = \frac{1}{4\pi^2\kappa^2} \int\limits_0^\infty \frac{\sin(\kappa R)}{\kappa R} \frac{\partial}{\partial R} \left[ R^2 \frac{\partial D_n(R)}{\partial R} \right]\mathrm dR](https://moodle.thga.de/filter/tex/pix.php/f7ca1875f6c0f2f1e7b888ac8212faed.png)
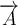
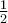
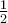
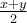
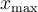
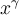
![A \xrightarrow[\text{unten}]{\text{oben}} B A \xrightarrow[\text{unten}]{\text{oben}} B](https://moodle.thga.de/filter/tex/pix.php/30427ad6014e8ba4ffeb75836701191a.png)
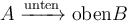
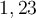
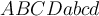
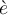
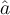
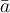
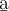
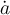
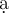
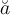

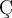
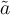
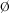
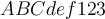
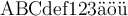
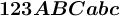

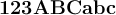
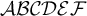
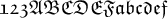
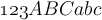
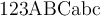
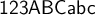
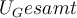
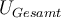
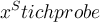
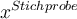
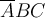
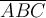
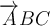
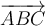
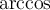
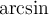
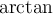
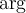
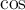
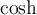
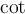
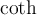
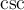
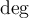
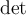
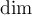
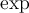
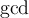
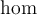
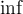
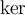
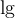
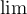
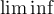
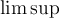
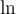
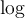
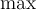
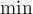
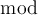
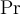
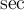
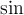
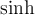
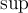
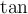
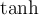
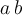
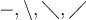
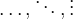
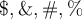


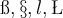
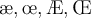
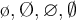
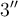
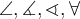
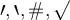
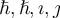
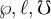
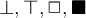

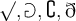
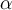
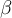
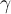
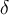
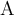
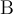
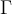

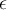
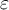
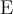
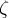
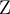
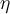
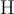
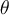
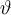
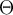
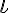
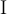
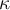
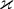
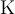
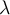
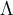
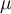
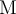
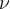
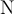
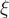
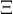
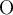
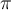
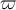
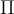
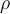
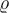
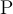
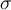
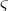

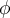
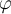
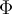
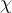
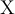
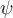
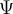
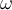

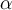
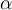
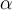
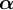
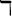

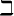
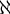
![[ ... ( ... \{ ... \langle ... \vert ... \|... \| ... \vert ...\rangle ... \} ... ) ... ] [ ... ( ... \{ ... \langle ... \vert ... \|... \| ... \vert ...\rangle ... \} ... ) ... ]](https://moodle.thga.de/filter/tex/pix.php/2ee3a7b00474924eae5c488372dca16d.png)
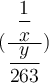
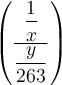
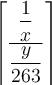
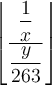
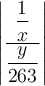
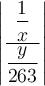
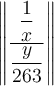
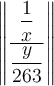
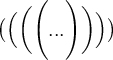
![\bigl[ \Bigl[ \biggl[ \Biggl[ ... \Biggr] \biggr] \Bigr] \bigr] \bigl[ \Bigl[ \biggl[ \Biggl[ ... \Biggr] \biggr] \Bigr] \bigr]](https://moodle.thga.de/filter/tex/pix.php/ff7f81262e9476c0e06cc937a19fb093.png)
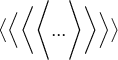
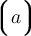
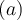
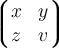
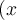
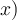
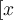
![\left. x \right] \left. x \right]](https://moodle.thga.de/filter/tex/pix.php/c30537bdf9a9fd331f0c16b00d0a72b0.png)
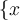
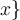
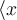
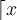
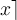
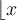
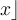
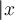
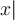
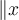
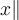
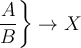
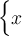
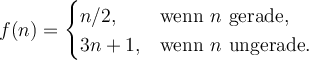
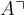
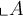
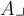
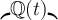
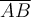
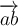
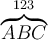


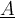
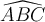
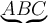
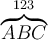
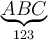
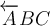
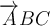
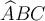
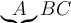


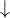



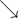
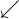

























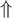






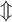
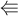













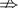
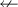
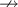
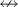


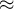

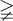
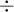

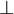
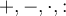
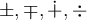
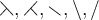
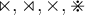

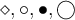
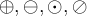
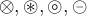
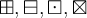
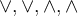
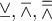
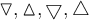
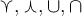
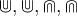
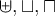
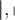
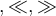

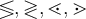
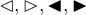
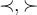
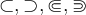
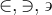
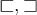
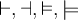
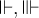
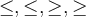

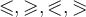
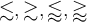
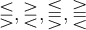
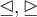
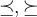
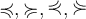
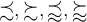
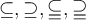
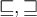
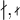
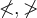
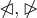
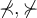
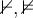
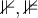
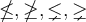
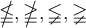
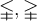
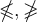
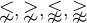
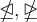
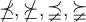
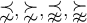
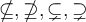
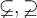
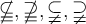
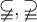

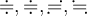
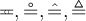
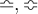
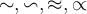
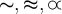

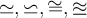
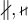
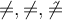
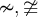
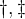
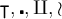
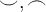

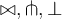
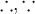
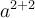
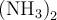
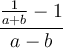
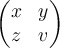
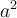
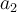
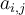
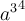
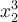
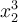
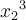
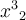
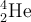
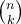
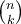
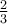
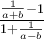
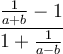
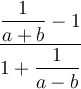
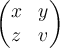
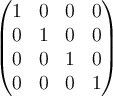
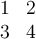
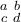

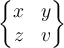
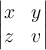
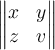
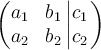
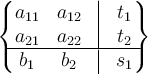

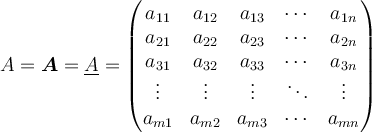
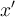
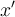
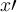
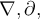
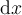
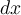
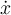
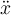
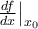
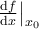
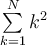
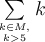
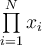
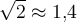
![\sqrt[n]{x} \sqrt[n]{x}](https://moodle.thga.de/filter/tex/pix.php/13fcbed8bcac58d95c0cb989f3aca2de.png)
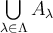
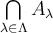
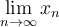
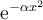
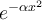
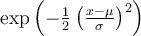
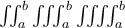
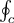
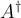
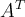
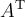
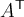
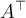
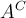
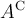
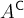
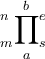
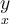
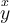
![A \xleftarrow[P+1]{n+\mu-1} B \xrightarrow[T]{n\pm i-1} C A \xleftarrow[P+1]{n+\mu-1} B \xrightarrow[T]{n\pm i-1} C](https://moodle.thga.de/filter/tex/pix.php/63dac46554dfdf1f3007f6857b65f46c.png)