Mathematische Grundlagen

Nach diesem "Warmup" hoffen wir dass das Memory etwas Spaß gemacht hat und du herausfinden konntest, wie fit du im Ausmultiplizieren von Termen bist und wo du vielleicht noch Schwächen hast, die du nun mithilfe von PepperMINT ausmerzen kannst ! 🥳

Für die kommenden Aufgaben solltest du dir bei Bedarf Stift und Papier herauslegen 📝

Die drei binomischen Formeln lauten: 

• Erste binomische Formel: $(a + b)^{2}=a^2+2ab+b^2\$
• Zweite binomische Formel: $(a - b)^{2}=a^2-2ab+b^2\$
• Dritte binomische Formel: $(a + b)(a - b)=a^2 - b^2\$

Erste binomische Formel: $(a + b)^{2}=a^2+2ab+b^2\$

Rechnerische Methode:

Rein rechnerisch kannst du die erste binomische Formel selber prüfen indem du den Term (a+b)² ausmultiplizierst. 

Der Rechenweg sieht dann so aus: 

In einem ersten Schritt kann das Quadrat (a+b)² zerlegt werden: 

$(a + b)^2=(a+b)(a+b) \$

Die Klammern können nun aufgelöst werden:

$(a + b)^2=(a+b)(a+b) = a^2 + ab + ba + b^2 \$

Die zwei Produkte ab und ba lassen sich zusammenfassen zu 2ab und wir erhalten das Endergebnis:

$(a+b)^2 = (a+b)(a+b) = a^2 + ab + ba + b^2 = a^2 + 2ab + b^2\$

Grafische Methode:

Anschaulicher wird es wenn du die erste binomische Formel an einem Quadrat mit der Seitenlänge (a+b) betrachtest.

Die Gesamtfläche A des Quadrats ist die Summe aus den Teilflächen a², ab, ba und b² . 

Addiert man die Teilflächen und fasst man die Summanden zusammen ergibt sich: 

Gesamtfläche A = Summe der Teilflächen = a² + ab + ba + b² = a² + 2ab + b²

Zweite binomische Formel: $(a - b)^{2}=a^2-2ab+b^2\$

Rechnerische Methode: 

Um die zweite binomische Formel rechnerisch herzuleiten, musst du den Term (a-b)² ausmultiplizieren.

In einem ersten Schritt kannst du das Quadrat (a-b)² zerlegen: 

$(a-b)^2 = (a-b)(a-b)$

Die Klammern kannst du nun auflösen: 

$(a-b)^2 = (a-b)(a-b) = a^2 - ab - ba + b^2$

Die zwei Produkte -ab und -ba lassen sich zu -2ab zusammenfassen und wir erhalten: 

$(a-b)^2 = (a-b)(a-b) = a^2 - ab - ba + b^2 = a^2 - 2ab + b^2$

Dritte binomische Formel: $(a + b)(a - b)=a^2 - b^2\$

Rechnerische Methode: 

Ähnlich wie bei den ersten und zweiten binomischen Formeln, multiplizieren wir das Produkt (a+b)(a-b) miteinander: 

$(a+b)(a-b) = a^2 - ab + ba - b^2$

Die beiden Ausdrücke -ab und ba werden voneinander abgezogen und wir erhalten als Ergebnis: 

$(a + b)(a - b) = a^2 - ab + ba - b^2 = a^2 - b^2$

Die drei binomischen Formeln dienen zur Vereinfachung von Termen. Sie können sowohl zum Ausklammern  als auch zum Faktorisieren angewendet werden. 

Beispiel 1: 

Wie lässt sich der Term (3x+2)² ausmultiplizieren?

Lösung: 

Der Term (3x+2)² entspricht der ersten binomischen Formel mit a = 3x und b = 2.

Wir erhalten dann : (3x+2)² = (3x)² + 2*3x*2 + 2² = 9x² + 12x + 4

Beispiel 2: 

Wie kann man den Term 4x²- 9 ausklammern? 

Lösung: 

Der Term entspricht der dritten binomischen Formel mit a = 2x und b = 3. 

Wir erhalten dann: 4x²- 9 = (2x)² - 3² = (2x - 3) * (2x + 3)

Beispiel 3: 

Wie lässt sich 17² ohne Taschenrechner berechnen? 

Lösung : 

Der Term 17² lässt sich in der Form umwandeln: (10+7)²

Mithilfe der ersten binomischen Formel können wir den Term ausmultiplizieren und erhalten: (10+7)² = 10²+2*10*7+7² = 100+140+49 = 289

Beispiel 4:

Wie lässt sich das Produkt 53*47 ohne Taschenrechner berechnen? 

Lösung: 

Das Produkt 53*47 lässt sich in der Form umwandeln: (50+3)*(50-3)

Mithilfe der dritten binomischen Formel können wir den Term ausmultiplizieren und erhalten: (50+3)*(50-3) = 50² - 3² = 2500 - 9 = 2491

Bevor wir mit den Regeln zur Bruchberechnung richtig loslegen, gibt´s erstmal Schokokuchen 🎂 und Orangensaft 🥃. In diesem Bruchrechenspiel kannst du durch Kombinieren von Formen und Zahlen Sterne ✨ gewinnen. Na looos, wie viele kannst du sammeln? 💪

  $\frac{5}{7}+\frac{3}{7}=\frac{8}{7}$  oder  $\frac{5}{7}-\frac{3}{7}=\frac{2}{7}$

Die einfachste Methode ist: den ersten Zähler mit dem zweitem Nenner multiplizieren und den zweiten Zähler mit dem erstem Nenner multiplizieren.



Wir erhalten dann: 

$\frac{20}{28}+\frac{21}{28}=\frac{41}{28}$

Wie kann man mehrere Brüche addieren oder subtrahieren? 🤔

Potenzen werden überall gebraucht. Damit kannst du Volumen, Flächen oder Zinsen berechnen. 

Dabei geht es darum, eine Zahl mit sich selber mehrmals zu multiplizieren. Die untere große Zahl nennt sich Basis und die obere kleine Zahl nennt man Exponent. 

Praxisbeispiel:

In einer Hydraulischen Presse wandelt sich Graphit in Diamant bei einem Druck von bis zu 6 Milliarden Pascal um. 

Problem: Eine 6 mit 9 Nullen... da hat keiner Bock drauf, oder? 😒

Lösung: Um diese Größe übersichtlicher darzustellen nutzt man die wissenschaftliche Schreibweise. Diese sieht dann so aus : 6*10⁹ Pascal.

Dabei werden Zahlen als Produkt aus einer rationalen Zahl und einer Zehnerpotenz dargestellt. Der erste Faktor wird dabei als Mantisse, die hochgestellte Zahl des zweiten Faktors als Exponent bezeichnet. 

Um Terme mit Potenzen zu berechnen, sind folgende Regeln zu beachten: 

Regel Nr. 1: 

Bei der Multiplikation zweier Potenzen mit gleicher Basis, wird die Basis beibehalten und die beiden Exponenten addiert. 

Formel: 

$x^n \cdot x^m = x^{n+m}$

Beispiel: 

$2^2 \cdot 2^3 = 2^{2+3} = 2^5 = 32$

Regel Nr. 2: 

Bei Potenzen mit gleichen Exponenten aber verschiedenen Basen, werden die Basen miteinander multipliziert. Der Exponent bleibt dabei unverändert erhalten. 

Formel: 

$x^n \cdot y^n = (x \cdot y)^n$

Beispiel: 

$3^3 \cdot 2^3 = (3 \cdot 2)^3 = 6^3 = 216$

Regel Nr. 3: 

Potenzen werden potenziert, indem der innere Exponent mit dem äußeren multipliziert wird. Dabei bleibt die Basis gleich. 

Formel: 

$(x^n)^m = x^{n \cdot m}$

Beispiel: 

$(2^2)^3 = 2^{2 \cdot 3} = 2^6 = 64$

Regel Nr. 4: 

Wenn ein Bruch aus Potenzen besteht, die den gleichen Exponent haben, werden die Basen durcheinander dividiert. Der gemeinsame Exponent wird dabei als Hochzahl genutzt. 

Formel: 

$\dfrac{x^n}{y^n} = (\dfrac{x}{y})^n$

Beispiel: 

$\dfrac{6^2}{3^2} = (\dfrac{6}{3})^2 = 3^2 = 9$

Regel Nr. 5: 

Besteht ein Bruch aus Potenzen mit gleichen Basen aber verschiedenen Exponenten, werden die Basen beibehalten und die Exponenten subtrahiert. 

Formel: 

$\dfrac{x^n}{x^m} = x^{n-m}$

Beispiel: 

$\dfrac{5^4}{5^2} = 5^{4-2} = 5^2 = 25$

Regel Nr. 6: 

Bei negativen Exponenten werden die Kehrwerte der Zahlen gebildet.  

Formel: 

$(\dfrac{x}{y})^{-n} = (\dfrac{y}{x})^n$

Beispiel: 

$(\dfrac{3}{5})^{-4} = (\dfrac{5}{3})^4$

Frage: Welche Zahl ergibt mit sich selbst multipliziert eine 9?  

Antwort: Die richtige Antwort ist 3. Die 3 ist also die Quadratwurzel aus 9.

Mathematisch ausgedruckt sieht es so aus : 

Dabei wird die 2 Wurzelexponent und die 9 Radikand genannt. 

Beispiel: 

$\sqrt[2]{9} = \sqrt{9} = 3$

Regel Nr. 1: 

Eine Wurzel kannst du in eine Potenz umwandeln. Dabei entspricht der Nenner des Bruches dem Wurzelexponent (hier n) und der Zähler der Hochzahl des Radikanden (hier m).

Formel: 

$\sqrt[n]{x^m}= x^{\frac{m}{n}}$

Beispiel: 

$\sqrt[2]{4} = 4^{\frac{1}{2}} = 2^{\frac{2}{2}}=2$

Regel Nr. 2: 

Wurzeln mit gleichen Exponenten kannst du multiplizieren, indem du die Radikanden  multiplizierst und den Exponent beibehältst. 

Formel: 

$\sqrt[n]{x} \cdot \sqrt[n]{y}=\sqrt[n]{x \cdot y}$

Beispiel: 

$\sqrt[3]{5} \cdot \sqrt[3]{25}=\sqrt[3]{5 \cdot 25}=\sqrt[3]{5^{3}}= 5$

Regel Nr. 3: 

Wurzeln mit gleichen Exponenten kannst du dividieren, indem du die Radikanden dividierst und den Exponent beibehältst.

Formel: 

$\dfrac{\sqrt[n]{x}}{\sqrt[n]{y}} = \sqrt[n]{\dfrac{x}{y}}$

Beispiel: 

$\dfrac{\sqrt[2]{72}}{\sqrt[2]{2}}=\sqrt[2]{\dfrac{72}{2}}=\sqrt[2]{36}=\sqrt{6^{2}}=6$

Regel Nr. 4: 

Beim Potenzieren von Wurzeln, kannst du den äußeren Exponenten einfach unter die Wurzel ziehen. Dabei wird der Radikand auch potenziert.

Formel: 

$(\sqrt[m]{x})^{n}= \sqrt[m]{x^{n}}= x^{\frac{n}{m}}$

Beispiel: 

$(\sqrt[4]{5})^4 = \sqrt[4]{5^{4}}=\sqrt[4]{625}=\sqrt[4]{5^{4}}=5$

Regel Nr. 5: 

Wurzeln kannst du radizieren, indem du die Wurzelexponenten multiplizierst und den Radikand beibehältst.

Formel: 

$\sqrt[m]{\sqrt[n]{x}} = \sqrt[m \cdot n]{x}$

Beispiel: 

$\sqrt[2]{\sqrt[3]{64}}=\sqrt[2 \cdot 3]{64}=\sqrt[6]{64}=\sqrt[6]{2^{6}}=2$

Regel Nr. 1: $\sqrt[n]{x^m}= x^{\frac{m}{n}}$

Regel Nr. 2: $\sqrt[n]{x} * \sqrt[n]{y} = \sqrt[n]{x*y}$

Regel Nr. 3: $\frac{\sqrt[n]{x}}{\sqrt[n]{y}}=\sqrt[n]{x*y}$

Regel Nr. 4: $(\sqrt[m]{x})^n = \sqrt[m]{x^n}$

Regel Nr. 5: $\sqrt[m]{\sqrt[n]{x}} = \sqrt[m n]{x}$

Mit Hilfe von Gleichungen ausgedrückt könnte man sagen:

Du suchst in der Gleichung $z^{y} = x$ das $y$? Dann ist die Antwort: $y = \log_{z}({x})$ .

Mit einfachen Zahlen sähe es so aus:

$2^{y} = 8 \rightarrow y = \log_{2}({8}) = 3$. Du musst also die 2 mit 3 potenzieren, um auf 8 zu kommen, $2^{3}$.

Der Logarithmus funktioniert aber auch mit Kommazahlen und Brüchen. Nur null und negative Zahlen ($\leq 0$) kann man im reellen Zahlenraum in den Logarithmus nicht einsetzen, da diese nicht definiert sind. Außerdem darf die Basis nicht $\leq$ 0 oder exakt 1 sein. Digitale Rechner oder dein Taschenrechner zeigen dir in solchen Fällen einen Fehler an.

In unserem Beispiel wäre 2 die „Basis“ und 8 der „Numerus“. Man sagt also: Man nimmt den Logarithmus zur Basis zwei für den Numerus (oder oft einfach nur „der Zahl“) acht. Die meistbenutzten Basiszahlen sind wohl 10, 2 und $e$, die eulersche Zahl (~2,7). Den Logarithmus einer Zahl zur Basis 10 nennt man „dekadischen Logarithmus“, den zur Basis $\textbf{e}$ nennt man den „natürlichen Logarithmus“. Oft werden verschiedene Kurzschreibweisen benutzt, wie lg() für den dekadischen und ln() für den natürlichen Logarithmus.

Rechenregeln für Logarithmen

Umkehrfunktion:
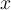Man kann den Logarithmus als eine Umkehrfunktion zum Potenzieren verstehen. Wir haben eben gesagt, dass ln() einen Logarithmus zur Basis $e$ bezeichnet. Wenn wir uns jetzt also vorstellen, wir würden $e^{ln(x)}$ haben, dann würden sich das Potenzieren und das Logarithmieren aufheben, und das Ergebnis ist einfach nur $x$. Dasselbe funktioniert mit $ln(e^{x}) = x$. Wenn also die Basis des Logarithmus und die Basis der Potenz identisch sind (hier: $e$), dann heben sie sich auf.  

In der Bauindustrie prüft man beispielsweise mittels sogenannte Sondierbohrungen ob der Baugrund tragfähig ist. Mithilfe von Sprenglochbohrungen können beim Bau von Verkehrswegen in felsigem Untergrund kleine Sprenglöcher gebohrt werden um Hindernisse zu beseitigen. Mittels Injektionsbohrungen können Abdichtungen vor fließendem Wasser errichtet und somit Bauwerke auch nachträglich abgedichtet werden. Baugruben, Talsperren und Brückenpfeiler können abgesichtert werden, indem man mittels Ankerbohrungen Ankerkonstruktionen in das Bohrloch einbringt und befestigt.

Im Bergbau, Tunnel- und Stollenbau werden zum Beispiel Aufschlussbohrungen - die sowohl senkrecht auf- und abwärts als auch horizontal oder geneigt gebohrt werden - zur Erkundung von Kohlenwasserstoffen (z.B. Öl, Gas), Mineralien (z.B. Erze, Salze) und zur Speicherung von gasförmigen und flüssigen Produkten (z.B. Wasserstoff, Helium, Erdgas, Erdöl, usw.) im Untergrund genutzt. Mittels Schachtbohrungen werden für den Bergbau, die Kalk- und Zementindustrie Großbohrlöcher gebohrt, verrohrt und später als Versorgungs- oder Fahrschächte genutzt.

Bei der Erschließung des Untergrundes mit Einzelbohrungen und mehreren Bohrungen muss darauf geachtet werden, dass ein dreidimensionales Verständnis des Bohrloches vorhanden ist. Das dreidimensionale Verständnis ist wichtig, da ein Bohrloch nicht perfekt senkrecht nach unten gebohrt wird sondern auch bewusst abgelenkt ("schräg") gebohrt werden kann. Insbesondere wenn mehrere tiefe Bohrungen gebohrt werden ist es wichtig, dass sich die Bohrungen im Untergrund nicht treffen. 

Bohrungen dienen jedoch nicht nur der Erkundung von Materialien sondern können auch zur Rettung von unter Tage eingeschlossenen Bergleuten oder Tunnelbauer:innen dienen. Mit Hilfe von Suchbohrungen wird nach den vermissten Personen gezielt in Räumen gesucht, die als Fluchtorte in Frage kommen. Hat man die Personen gefunden kann man sie zunächst mittels Versorgungsbohrungen versorgen bis die Bergungsbohrung fertiggestellt ist. Mittels sogenannte Rettungsbomben werden die Eingeschlossenen durch das Bohrloch geborgen. Die wohl bekannteste Rettungsbombe ist die Dahlbuschbombe, die auf dem Bergwerk Dahlbusch in Gelsenkirchen entwickelt wurde.

Weitere Anwendungsfälle für die Durchführung von Bohrungen sind die Wasserversorgung und der Brunnenbau, das Entwässern von Tagebauen oder das temporäre Absenken des Wasserspiegels bei der Erstellung von Bauwerken, das Einrichten von Grundwassermessstellen zu Kontrollzwecken, die Erkundung neuer Deponie-Standorte oder Lagerstätten, die Stabilisierung von Untergrund u.v.m.

Berechnungen bei Bohrarbeiten